Zarlino 1558, Le institutione harmoniche, part 2
English translation © 2003 by Leonardo Perretti
webpage © 2003 by Joe Monzo
How whatever musical interval could be divided in two equal parts. Cap. 24
It would be very useful for our purpose (if we want to show how
whatever musical interval could be divided in two equal parts) the
Ninth of the Sixth of Euclides, according to Campano; or the 13. and
fifth problem after Theon, that says: Given two straight lines, we
can find the line of the proportional half; that is like to say, that
given two sounds, we can find a sound at the proportional center
between them; and this is the way.
Let us suppose that in the example in the figure the octave consonance is settled at its proportion, between the string ab, and the cb, and it is needed to find a middle string, that, between these two, it divides them geometrically in two equal parts.
First, we will lengthen the line ab, beginning from the point toward the right direction, until the point d, in such a way, that bd is equal to cb, and we will have the ad.
This made, we will trace a semicircle, which diameter is all ad, then we will draw a line, that starting from the point b, where the said ab is joint to bd, goes perpendicularly to the circumference of the semicircle to the point e: and it will be be; and this will be the sought middle string.
And in order to demonstrate this, I will draw the line ae, and the ed, and the triangle aed will come, that is called right-angle [Orthogonio], which, (as for the 31. of the third of Euclid is clear) is of such a nature, that it has a right angle, that is the angle e: Therefore, being this triangle divided by the line eb, that is drawn perpendicularly from the circumference of the semicircle in the right angle at its base, as can be seen in the figure.
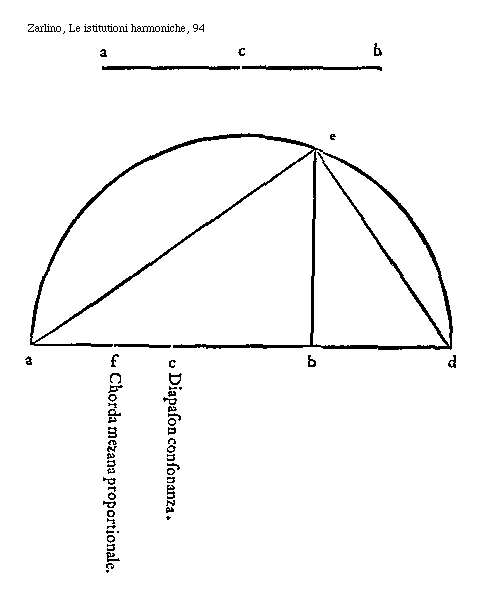
Two minor triangles come, the one greater than the other; that are the abe and the ebd, in kind and nature similar at all to the triangle aed, and they are proportionate the one with the other, as it is known by the Eight of the Sixth book of the Elements of Euclid.
And as a corollary of that preposition, the proportion of the ab to the be, is the same, that is from the be to the bd, according to our purpose. Now, making the fb equal to the be, we will have the equal division of the proposed consonance from the string fb, as required.
And who wants to see the proof of this operation, could divide the double octave by the shown mode: then he will know, that the middle string, that divides it in two parts, will be equally spaced, as much from the extreme low string, as from the extreme high of that consonance, for an octave, according to the purpose.
--------------------------
Another method for dividing whatever consonance, or musical interval in two, or more equal parts. Cap. 25
The other method of dividing the consonances, in two, or in so many
parts one wants, being equal, is not only beautiful: but also more
useful then the preceding, for being more universal; and it was
discovered by Eratosthenes, when he found the duplication of the
cube, at the time when the Dalij (as Johannes Philoponus [Giovanni
Grammatico] narrates) were troubled by the plague; the same
invention, together with many others, Giorgio Valla from Piacenza put
in the "Fourth book of the Geometry", teaching how to find two middle
lines between the given two. It is well true, that without the help
of an instrument, something called a
mesolabium,
whatever effort would
be vain and useless; but before I go more ahead, I will show the way
to build the instrument; and then I will teach how to find the lines.
So, first a board, or table must be prepared, well leveled, and
smooth in its surface, being almost one foot wide, and as long as one
wants; although the more it is long, the more comfortable it would
be.
Then, after having shaped it as a square long figure, that contains at its corners four right angles (in order to operate more comfortably, and without any error) we will diligently make a channel on it, by putting sides longways the said board or table, two rulers, or thin lists made with moderation, so that being they equidistant, the sides of the channel are as high as the back of a knife, and not more.
This made, we will make three square figures of metal, or very thin wood, that geometricians call Parallelograms, having four right angles, and be as long as the channel is wide, and wide at will, provided that they are made in such a way, that the one is equal to the other, i.e., that the sides of the one are equal to the sides of the other.
Then, on two of them we will draw a diametrical line from the upper left corner to the lower right corner of each of them in such a way, that the surfaces are divided in two equal right-angled triangles, as can be seen here.

Then, we will place the squares in the said channel one after the other in such a way, that the first without the diameter be on the left side, and remains immobile; then the others, that have the diameters, i.e. the second, and the third in order on the right side, so that the right side of the one is placed on the left side of the other; and so we have made the instrument. It is defg: and hikl is the first immobile square with no diameter [diagonal]; the second nopq, which diameter is nq, and the third is rstu; of which ru is the diameter.
Let us suppose now that it has to be found, a middle proportional string, that would divide in two equal parts the octave consonance, containing the double proportion [2:1], between the two strings, or lines ab and cb; and these are equal to the ab and the cb we put in the previous chapter.
First, we will make the right side of the first square, i.e. lk, equal to ab in the point m, and this will be lm.
Then we will take the second square, and push it under the first so much, that its diameter nq would cut the side kl of the first square in the point m; and so the first and the second square will remain still.
Then, we will make the right side of the third, that is ut, equal to cb in the point x; and place a very thin wire in the point m, that is the mx of the submitted example, we will draw it so much, that it crosses the point x.
We will now push the third square under the second so much, that the side pq comes to be cut by the diameter ru, and by the mentioned wire in one point, that will be y; and that part of the right side of the second square, that remains under the wire, that is the qy, will be the sought line, or proportional string; as in the figure is shown.

-
[Below is a version of the above diagram in which
the "squares" have been shaded in light grey, and
imagined to be of translucent material so that when
one "square" is slid under another, the two shadings
combine to form a darker shade of grey, thus helping
to visualize the placement of the three "squares".]
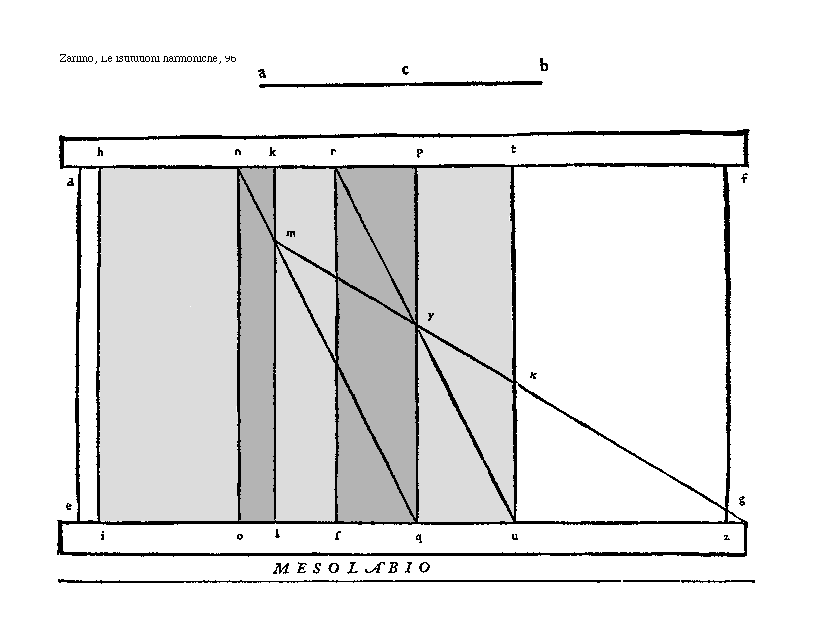
And this is clear from the previous demonstration: as the middle proportional line qy found in the mesolabium between the ab and the cb is equal to the be we found in the previous chapter. This could be demonstrated, if one would draw on a flat surface all the lines made on the Mesolabio, drawing first as for the Second definition of the first [book of the "Elements"] of Euclid, the line mx until the point z: as then we would have three triangles containing a right angle, that is lmz, qyz and uxz: from which it could be demonstrated that this all is true according to the Principles and Demonstrations of Euclid; as well as to the Second common notion, and the ninth for the 28, and the Second part of the 32. of the first: to the second, the fourth, and the sixth of the Sixth; and the eleventh of the Fifth; that I let apart: as I have extensively talked about them in our "Demostrazioni harmoniche". It will then be enough to say just, that if one should want to divide in multiple parts whatever musical interval, he has to use the shown procedure.
It must be warned, that for each line, or string that one would add in addition to the found one, it will be needed to add another parallelogram, or square with its diameter, made in such a way, and size, as the previous; being then careful, that the right sides of each square be marked in the same point by the diameters, and by the wire according to the shown mode. Having care to put constantly the first square without the diameter, that must be immobile, and that its right side be cut by the diameter of the following on that point, that will be put by the length of the proposed major line; and that the right side of the final [square] be cut by the wire in that part, that is equal to the length of the minor proposed line, according to the given mode. And if the major given line would be longer then the square of the Mesolabio, nothing could be made. But it is well true, that taking the half, of each of the two proposed [lines], one could obtain his goal: because after having made all, the middle found [lines] could be lengthen according to the ratio of the taken part of the proposed lines; and so everything would return well.
--------------------------
What must be observed in tempering, i.e. tuning the intervals of each modern artificial instrument, reducing the number of the strings of the Diatonic syntone to that of the Diatonic; and that those intervals are not natural, but artificial. Cap.42
In order that the reader scholar knows why, and by what quantity each
interval should be tempered in the mentioned instruments, and how
should he proceed, if he wants to make the temperament
[Partecipatione], in a manner that it does not offend the feeling (or
hearing), I will start the job now; and in the same time I will show
the manner by which the 17 strings, put in the Diatonic syntone, are
reduced to the number of the 16 contained in the Diatone.
But it must be considered, that if one wants to make the temperament or "Partecipatione" with a good reason, and with solid ground, it is necessary to divide the comma, contained between the strings RB and MB in seven equal parts, and distribute them between the seven intervals, contained in the eight strings of the Octave (Diapason); so that we can reduce the two mentioned strings, that contain the comma, to only one. But is should be done, so that the intervals remain in their proper shape as much as possible; so that the Hearing doesn't be offended: and that each consonance, both in the bass and in the treble; and whatever other interval, however small be equally augmented, or diminished by a given, and determined quantity, in all those intervals, that are similar in proportion.
This will turn very useful, when we will act in such a way that each fifth (Diapente) be diminished, and imperfect, of two seventh parts of the comma; and that the fourth (Diatessaron) be augmented of the same quantity; and it is a duty: since the octave must remain unmodified, and with its true and natural proportion, and since it is made out of these two parts, what is subtracted from the one, must necessarily be given to the other; so that by their addition, at the ends the perfect octave be heard.
The major-3rd (Ditono) will be made imperfect by one seventh, and also the minor-3rd (Semiditono) will be diminished by the same quantity: As if these two consonances contribute to the formation of the fifth; being this diminished by two seventh parts, it is necessary, that that amount be distributed between these two intervals: as if one makes the third imperfect of one seventh, and the minor third of the same, that together give two seventh parts; these two consonances, that are part of the fifth, are diminished of the same quantity, by which their All is diminished.
But the parts of the third, that are the major and the minor tone, will be made imperfect as follows: from the former four seventh of the comma will be taken away, and the latter will be increased by three; and so they together will have the same imperfection, that has their All; i.e. they will be imperfect of one seventh part.
Then, the major semitone will be increased of three seventh parts: as it is the smaller part of the minor third, and the major tone the greater, with those two parts the same diminishment will be found, than in the minor third, i.e. they will be diminished.
The major-6th (Essachordo), and the minor-6th, both will be increased of one seventh part, as the former is made of the 4th and the major-3rd, the latter similarly of the 4th and the minor-3rd: since the 4th is increased of two parts, and the major-3rd and minor-3rd both of one seventh part, the 6ths are truly increased by that amount.
After having made the instrument proportionate as described, setting the octave apart, and the shown minor semitone will be out of its true proportion, but not much far from its true shape, so that the Hearing is not satisfied. This is, then, what must be observed, if we want the temperament, or distribution of the comma, in every instrument of ours; so that every consonance in its kind is equally augmented, or diminished. Therefore every expert in sound must be diligent in that, if he wants to temper, or tune the above mentioned instruments, of necessity he will have to pull, or proportionate each fifth in such a way, that its high ends be kept from the low, according to the amount I have talked above, that I will show soon; or the low will near to the high, according to the best convenience in tuning or tempering the mentioned instruments. In the same way, each fourth, to which are given the amounts, that are taken away from the fifth, has to be augmented in such a way, that every high extremity is far from the low for the same quantity, and similarly the low from the high.
And notwithstanding this way these intervals are now increased, now diminished, nevertheless the Hearing (as I said) does not abhor that distribution: since the quantity that is taken away or added to those intervals is very small, and almost insensible, and since they are not so far from their true form, the sense quietens. Nor should we marvel of that, since the same happens to the Hearing, then to the other senses, and above all the Sight, that sometimes does not becomes aware of a minimal quantity, being almost insensible, as it happens; as if one takes away, or adds to a big heap two, three or more fistfuls of corn, he doesn't notice it: while he would well notice, if one would remove or add a great quantity.
But if someone would affirm, that using the consonances, that are out of their true proportions, which, out of doubt, are not lacking of sweetness, that the true, and right consonant intervals are these, and not those that I mentioned above, he would be really wrong: although the already shown intervals could not be found in the above mentioned instruments; it does not prevent them from being the true, and natural, and those that perfectly generate every consonance that could be generated.
It also follows, that they could not be produced, and heard: but they can be heard whenever is needed; as similarly it does not mean that a man be unable to laugh, just because he does not laugh all the time; because although he does not laugh now, he is able to laugh whenever he wants.
And although by the mentioned instruments, tempered as described, one cannot use the consonances in their perfection, i.e. in their true, and natural form; nevertheless it is possible to use them, if one would pull the strings under the ratio of their true, and natural proportions. And I can say that, because many times I made the experience on an instrument, that I had made for that purpose; and that test can be made on whatever instrument as well, and mainly on [arpichordi] or Harpsichords, that are well suitable for the purpose.
And if someone would say, that if those instruments would be tuned perfectly, a lot of consonances, that can be found in other instruments, would go lost; this doesn't matter: because it is enough to me, that no one could contradict with truth what I have said above, and affirm that those consonances cannot be made in their true forms, or proportions; as even if by them the harmonies could not be practised with the same comfort, and freedom, that in the common instruments can be found; [nevertheless] it would not descend, that by them every consonance, and every harmony could not be heard in its true form.
But if those drawbacks (so to say) are found in the artificial instruments, nevertheless, between Voices, as we will say again later, such respects aren't found: as they reduce everything to its perfection, as it is its duty: since the Nature, in making things, is far better then the Art: and the latter in imitating makes everything imperfect, and the former (the obstacles removed), reduces everything to perfection.
Then, each of the mentioned instruments will be tempered that way; in them the comma will be distributed in seven intervals, as I have said; nor it would result well otherwise, if one wants to acquire the perfect consonances, and the imperfects together, as best as it can be done; so that every similar interval, in the low as in the high, be equally increased, or diminished by its [proper] amount; and one would have no longer to put the string d duplicated.
And should someone find strange, that in the Music such things are needed, he would remember that not only in this science; but in every other science, in every art, and in every other created thing a big imperfection is found. And I think that this is the will of God the Best and Most High; so that by seeing the imperfection of those inferior things, we turn our intellect to the contemplation of his Infinite Wisdom, in which everything is found not only perfect, but also optimal.
--------------------------------------------------
Demonstration from which one can understand, that the shown temperament, or distribution is made in a reasonable manner; that it cannot be made otherwise. Cap.43.
-
[In the following discussion, the untempered JI tuning to
which Zarlino refers is set out in this diagram:]
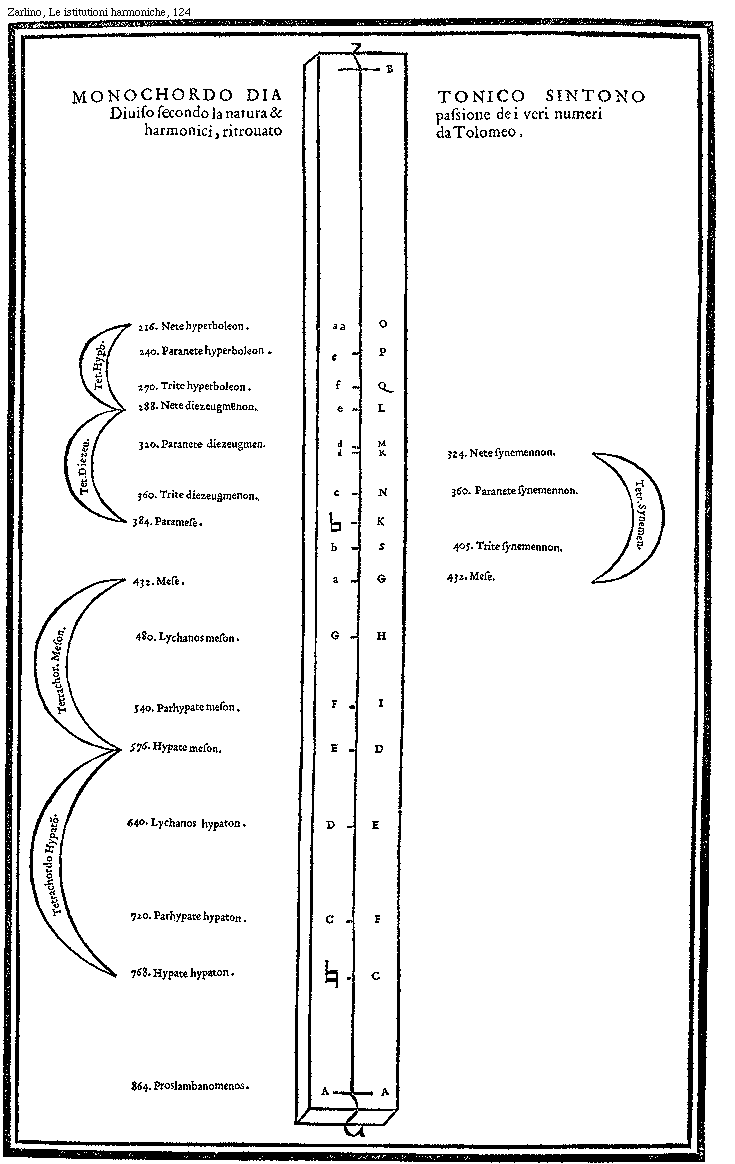
-
[Below is a table listing the pitches in this scale,
and a lattice diagram labeled with the string-lengths
specified by Zarlino.]
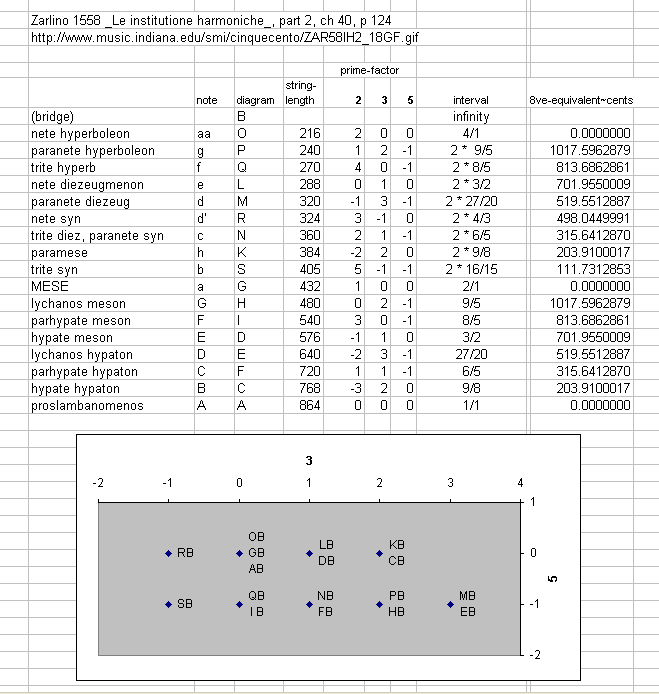
I will now demonstrate the reason of that temperament:
but it must be known, that there has been someone, who opined, that the interval of the comma shown above would be distributed between those two intervals, that are nearer to it, placed in the high, and in the low parts, making two equal parts of it, increasing the one, and the other interval of such a quantity, as is half the comma; then leaving the other intervals in their natural forms: but in truth it appears to me, that they are wrong for many reasons: first because those two intervals, that are near the comma, would be the sole to participate in the parts of the comma, and no one of the others, and the instrument would be unequally proportioned: as in it one would hear the fifth, and the fourth with two intervals one greater of the other, next, because those intervals, in which this distribution would be made, would be dissonant, because of the great distance, that they would have from their true forms; and the tones, that are near to the comma, and share one of its parts, would be contained in such a proportion, that they could not be added to the fifth, nor to the fourth, nor to the minor third to form any consonance.
And even if they say, that the experience shows, that these intervals, augmented or diminished in such a way, are not so far from their proper form, so that the hearing would not be offended more than would happen, if the comma would be distributed in a different manner; this is not true. Therefore I think, that they never tested it: as the feeling itself makes it clear, that they are dissonant; and everybody could demonstrate it by himself, by dividing the mentioned comma in two equal parts, the way I have demonstrated in the cap. 24 above: therefore after having added the two derived parts to the two [Sesquinoni] (=10/9)tones, that are next to it, everybody will know, that what I have said is the truth, and that it is necessary to try to distribute that comma in a different manner, so as the Hearing would not be offended.
But since I said above, that some of the consonances, or other intervals, are diminished (by making this distribution) by two, some by four, and some by one seventh part of the mentioned comma: in the same way some of them are increased by one seventh part, some by two, and some by three parts: in such a way that not only every fifth, every fourth, every major third, and every minor third, that are consonant intervals, are equally increased or diminished, and remain equal in the low part, as well as in the middle, and in the high part of the instrument; but also the dissonant [intervals], that are the major and minor tone, and the major and minor semitone.
But I will maintain this as much a truth, as a manifest sign demonstrates, that this distribution is good, and made with the greatest diligence: indeed the minor semitone, that is contained in the [Super 7. partiente 128] (=135/128), that isn't used in the Diatonic genus, and is contained between the strings SB and KB, is made minor by all the parts, i.e. by the entire comma, that is contained entirely in the [Sesquioottantesima] (=81/80) proportion; and so it remains in the [Sesquiuentesimaquarta] (=25/24) proportion. Therefore its proportion remains rational, then the remaining, setting apart all the octaves, that are made of the double proportion, are irrational and unknown: as the parts, that are subtracted, or added to the rational quantities, which are their first natural forms, are irrational when the division of the All in parts is irrational, and what derives is similarly irrational. And since is as well irrational, what derives from the addition or subtraction of a rational quantity from an irrational one: in the same manner it is irrational what derives from the subtraction, or addition of an irrational proportion from a rational one. But this does not happen for the rationals: because all that derives, adding or subtracting one quantity from the other, is rational. The reason why this distribution, that is made by adding, or removing those parts, cannot be rational for any reason; nor it can be named or described by determinate numbers by no means: is that the division of the comma in seven equal parts is not rational.
Then, in order to demonstrate that it is convenient to make this
distribution in the mentioned manner, and not otherwise, we will
proceed by the following order.
-
[I have added lattice diagrams below which will be found helpful
in what follows.
They show the same JI syntonic diatonic lattice as in the
last diagram, but now also include the 2/7-comma meantone
chain from -2 to +5 generators centered on C = 0 generator,
which represents the 8 JI pitches and is the temperament described
by Zarlino. The green lines show portions of the syntonic comma and
connect the JI pitches to their tempered approximations.
Note that while Zarlino labeled his origin-point (n0 = 1/1) as "A", he begins calculating his meantone tuning with generator 0 labeled as "C" 31 5-1 (= 6/5), which are his string-lengths NB and FB, and states that this is common practice for tuning "artificial instruments", i.e., any musical instrument other than the voice; therefore, i have plotted the pitches according to n0 = A, but have labeled the meantone generators with generator 0 = "C".]
First, let us take only twelve strings
of the monochord above, i.e. FB, EB, DB, IB, HB, GB, SB, KB, NB, RB,
MB, and LB, that will be enough to demonstrate the purpose; and then
we will tune perfectly the strings FB and NB in such a manner, that
they contain the consonance of octave; we will let them immutable,
and on them we will start to make the distribution; although one
could begin from whatever strings he desires; but we make it this
way, in order to follow most of those, who tune the modern
instruments: as they begin from those strings. It is to be stressed,
that I have said immutable; being it a necessity, that the first
string upon which the distribution is based, be stable, and that each
octave be brought to its perfection, i.e. to its true form, that is
the double proportion: so as it doesn't suffer any alterableness or
variation. Then, given that we have these strings stable, by those
strings that are placed between them, we will make the distribution,
yet using the other strings, that are set outside them.
And to begin with, we will take the first fifth in the low, that will be the FB and HB, set in the [Sesquialtera] (=3/2) proportion; without moving the FB, we will make the HB lower according to the quantity of two seventh parts of the comma, as I said; first placing before, and multiplying to the string HB the comma, by first adding to the string IB the minor tone contained in the [Sesquinona] (=10/9) proportion, and dividing it in ten parts; then, taken nine parts of it, between the string that contains that quantity, and the HB, that is the high string of the major tone IB and HB, we will have the comma: as if from the mentioned tone we will take away the minor, that is IB, and the quantity of the nine parts, out of any doubt the comma will remain, consisting in the [Sesquiottantesima] (=81/80) proportion; that we will divide in seven equal parts, according to the method shown above in the cap. 25; then, letting apart the two higher parts of it, and maintaining on ly the five lower parts, by the string aB suddenly we will have settled to their irrational proportions two consonances, i.e. the fifth FB and aB, and the fourth aB and NB.
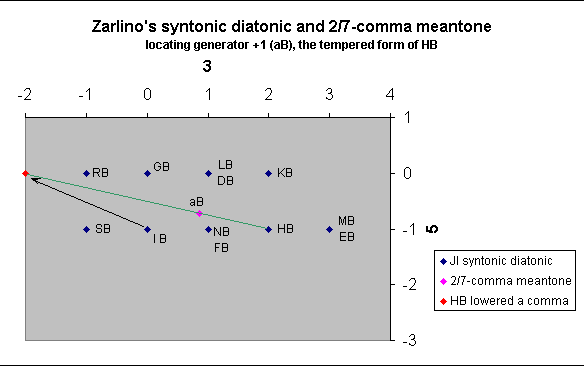
Now,
we will take the aB, that with the MB contains the fifth augmented by
two seventh equal parts of the mentioned comma; after having divided
the comma RB and MB in seven equal parts, as we made before, letting
apart the four higher parts, that are the two parts, that must be let
for obtaining the fifth in its true proportion, and two more parts
for its diminution; the string bB will give us our scope.
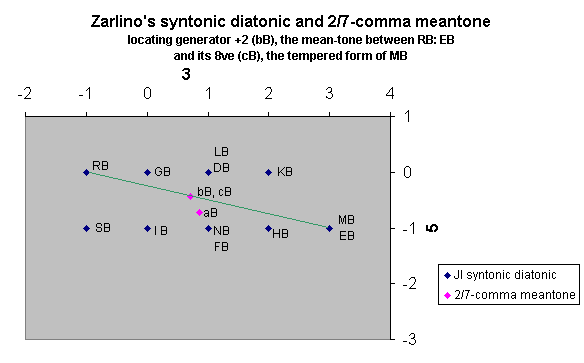
We will
find the correspondent to this string in the low in double
proportion, so that we can hear the octave perfectly; we will have
done it, when after having multiplied, and placed the comma before
the EB, and divided in seven equal parts, we take the four [parts]
placed at the high [extreme]: so between cB, and bB we will have the
sought consonance, with the half of cB according the purpose: since
EB corresponds to MB for having equal sound in the octave consonance;
and adding to both four parts of the comma, that are equal, to the
low [extreme], it follows, that in the same way the extremes of these
increased [intervals] are equal, and give the octave consonance: as
for the second and third common statement of Euclide's Elements, if
one adds or removes equal things to equal things, the result is
similarly equal. We will also have a fourth increased by two parts of
the comma between cB and aB, that will be equal in proportion to aB
and NB.
We will make now the string GB, corresponding in
[Sesquialtera] (=3/2) proportion to cB, adding to GB the comma,
dividing it according to the given mode; then letting the four parts
in the high, and the two, that follow in the low; between cB and dB
we will have another fifth diminished by two parts of a comma, and
between dB and bB another fourth increased by the same quantity.
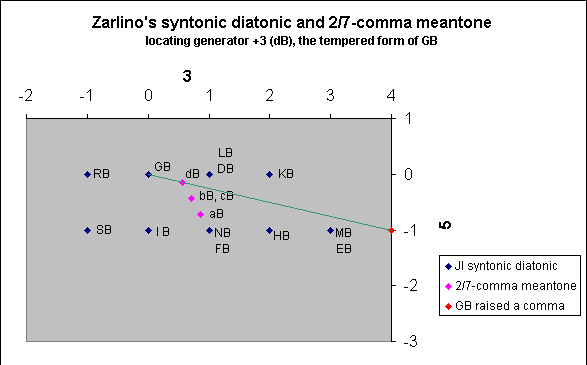
Then
follow the dB and LB, that contain the fifth diminished by one
seventh part; then if one wants to reduce it of one more part; so
that it becomes equal in proportion to the others; we will put the
comma before LB, divided in seven intervals as for the others, and
set apart the higher, we will take only the six in the low; and from
eB we obtain the purpose.
We will find the corresponding to this in double proportion, as follows; we will divide the comma put before DB in seven parts, then, taken the higher part, we obtain fB, that with the mentioned eB will give us the octave consonance in its natural form, and another fourth equal in proportion to the others, that will be fB and dB, in its accidental form.
Then, between fB and KB there is a fifth, similarly in its accidental form, higher by one of the mentioned parts, so in order to reduce it to its proportion, we will put the comma before KB, divided according to the given mode; and letting the higher part for the surplus, and the following two parts for the diminution, with half the string gB, we will obtain not only the true accidental proportion of the fifth; but also that of the fourth, contained between gB and eB.
It remains now to reduce to its proportion the fifth IB and NB, and the fourth FB and IB; so we will add the comma to IB, which, after having been divided in seven parts, and after we have taken the two lower seventh parts, by half the string hB, will give us the proportion of the mentioned consonances; i.e. we will have increased the fourth placed in the low by so much parts, and made smaller the fifth placed in the high by so much quantity.
Now, in order to give its proportion to the SB, that with respect to the hB is now one fourth diminished by two parts apart; we will add the comma to SB, and after having divided it we will take the lower four parts in the point I; and we have made the fourth between iB and hB equal in proportion to the others.
-
[The lattice below shows
the complete 2/7-comma meantone scale as described by Zarlino.]
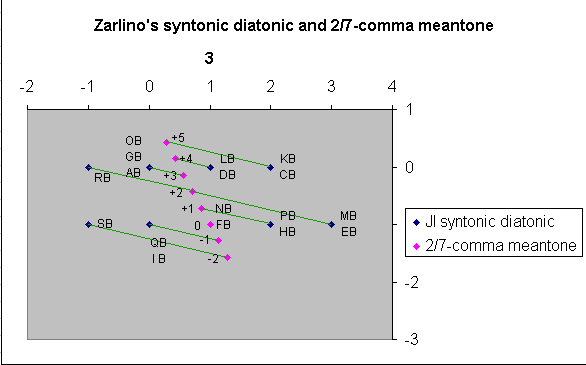
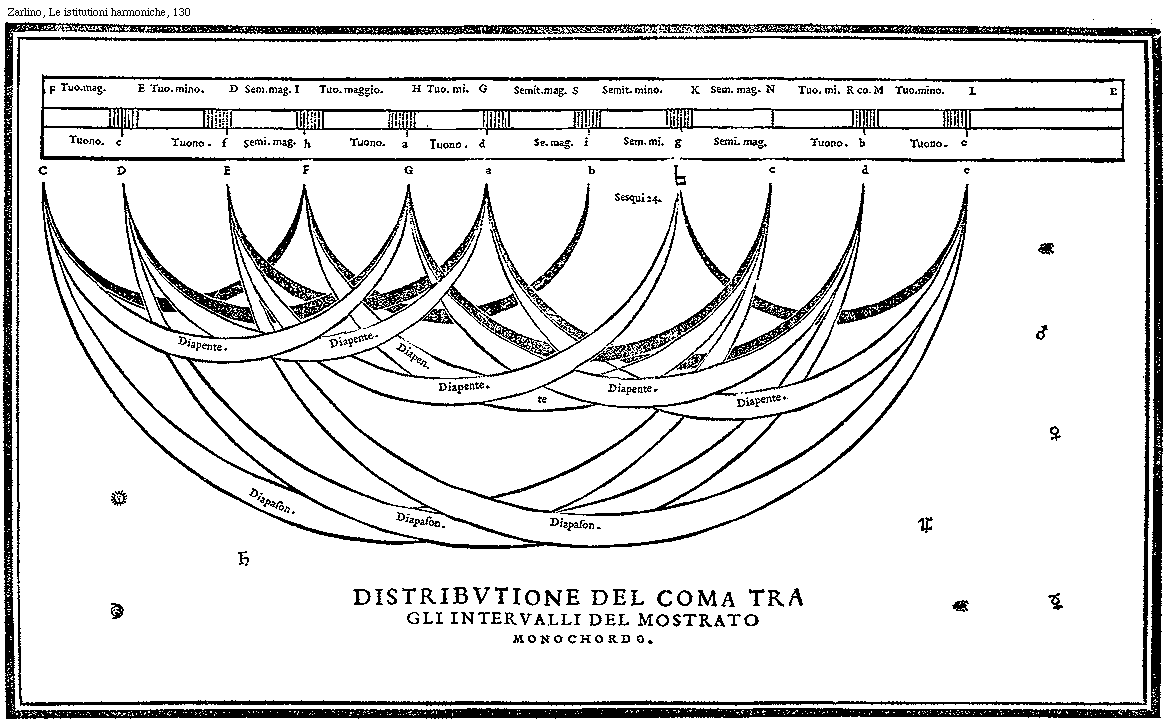
F major tone. E minor tone. D minor semitone. I major tone. H minor tone. G major semitone. S minor semitone. K major semitone. N minor tone. R comma. M minor tone. L B tone. c tone. f major semitone. h tone. a tone. d major semitone. i minor semitone. g major semitone. tone. b tone. e C D E F G a b y c d e Sesqui 24. Diapente. Diapente. Diapente. Diapente. Diapente. Diapente. Diapason. Diapason. Diapason. DISTRIBUTION OF THE COMMA BETWEEN THE INTERVALS OF THE SHOWN MONOCHORD.
By this method, then, we have
increased or diminished equally not only every consonance in its
kind; but every other interval, that was contained between the
mentioned strings; and of twelve strings that were before, we have
reduced them to the number of eleven, corresponding to the number of
the Pythagoric strings, put above in Cap. 28; that we could
conveniently describe by the letters of Guido [d'Arezzo],
without duplicating the d.
And what I said above about the minor semitone is verified; as since it is contained in its own proportion between the strings SB and KB, and being it diminished in the low (as it can be seen by the demonstration) by four parts of the comma, contained between SB and iB; and in the high by three parts, contained between gB and KB; if we will add these three parts to the previous four, there is no doubt, that they will reach the number of seven, and they will make the entire comma. But since (as I have stated elsewhere) the comma is contained in the [Sesquiottantesima] (=81/80) proportion, if from the [Super 7 partiente 128] (=135/128), that was the first form of the minor semitone, that is rational, we will take away the [Sesquiottantesima] (=81/80), that ia rational as well; the remaining will be the [Sesquiuentesimaquarta] (=25/24) rational proportion, that is the rational form of that semitone.
We can now see the manner by which the parts of the comma are distributed, with some equality, in every consonance, and every interval. This way we can be sure, that this methd is so much better, and truer, when we see that every consonance, and every interval, whether in the low, or in the middle, or in the [high] end, is increased, or diminished by the same quantity, according to what its proportion requires: nor it could be seen in no way, that one is major then the other, or minor: nor one could perceive, that there are any remainders however small, of any parts of the mentioned comma; because if some of these thing would be found, it would be a clear sign, that the distribution had not been made by the due method.
Therefore I conclude, that should one try to make the distribution otherwise, that that effort would be vain, and bring no result; as the experience will ever show. Then since this thing cannot be made otherwise, so that it would be suitable in the mentioned instruments; it follows that this temperament, or distribution should be made perfectly, by the due tools, and without any error.
----------------------------
About thickening the shown diatonic monochord, with the strings of the chromatic genus. Cap. 46
It remains now, that we see, how the above shown diatonic monochord could be usefully thickened, with the strings of the chromatic, and those of the enharmonic. But it must be noted, that since it has been added, in the shown composition, the synemmenon thetrachord to the meson tetrachord; because of such junction, the tone, that is placed between the string a and the string [sqb], is divided by the string b in two parts, i.e. one major semitone, and one minor; therefore casually another tetrachord comes, between the strings a. b. [sqb]. and d: because between the a and the b a major semitone is found; between the b and the [sqb] the minor semitone; and between the [sqb] and the d the trihemitone, as in the four strings below it can be seen. [image] Fourth. Tone. Major Third. d. Nete Synemmenon. Threehemitone. [sqb]. Paramese. Minor Hemitone. b. Trite Synemmenon. Major Hemitone. a. Mese And since that tetrachord in no way is similar to the diatonic tetrachords, put in the chap. 16 it cannot truly be said, that it is diatonic; but it can be well said that it is chromatic: indeed it is very near to Ptolemy's soft chromatic: as it proceeds from the low toward high by one semitone in the first interval, in the second similarly by another semitone, and in the third by one trihemitone, according to the form of the already shown chromatic tetrachords. So that we can truly affirm, that this is the true sought chromatic tetrachord, that is useful, and very necessary for thickening the shown diatonic monochord. And if anyone should say, that the Ancients put the minor interval in the lowest part of their tetrachords, and the others then according to the order of bigger interval; and that in it the major semitone is found first, and then the minor; I would reply him, that this is of small importance, as this is not made inappropriately: as such intervals are naturally placed, according to the way that is determined by the nature of the harmonic numbers, which give its parts in the low first, or the major intervals, and then ordinately the minors, so as we saw in the cap. 39 above. Then, we have to provide setting the intervals in such a way, that we can gain all those consonances, that are useful for generating the perfect harmony, and don't take care, that in the tetrachords the major interval is not placed before the minor, and then it follows that many consonances go lost. The Ancients well took such care, but they did not make their harmony the same way we make, and they had opinion, that the major intervals (as I already said elsewhere) were made with the minors. But we will see below, if it is more reasonable to say that the major intervals are built in that manner, or that the consonances, and the major intervals come from the minors. Then, if having put the major semitone before the minor has no drawback, as well it would not cause that that tetrachord is not chromatic; as it is not diatonic, nor enharmonic. Then, this tetrachord has the minor semitone between the string [ ] and the [ ], that is not used in the diatonic modulations, nor in the enharmonics; and between the string [ ] and the d, there is the uncompounded trihemitone, that in the diatonic is compound, that is contained in the sesquiquinta (6/5) proportion, similarly that same interval is contained in the high part of the soft chromatic of Ptolemy; as it could be verified by reducing the four shown strings to their proper forms, that are contained between the harmonic numbers; as in the chap. 15 of the first part, in the strings of the first tetrachord called hypaton, as in the picture below it could be clearly seen.
[image]
Diatessaron. Minor tone. Semiditone. 60. E. Hypate meson. Trihemitone. Sesquiquinta. 72. [ ] Lychanos hypaton. Minor semitone. Sesqui 24. 75. C. Parhypate hypaton. Major semitone. Sesqui 15. 80. [ ] Hypate hypaton.
And again, the fact that it is very different in the first two intervals from the soft chromatic, this still is of small importance, considering the little utility, that can be derived from those intervals since they cannot give any consonance, as it would be clear, if someone would want to use them. So, this tetrachord will have the form of the other four tetrachords, when we will want to thicken the monochord shown above in the chap. 40. It is well true that when [those tetrachords] containing such proportions would be put in such monochord, it would rather generate confusion then utility; because of the moltitude of the keys and strings, that would increase, in order to find the consonances according to the purpose, in addition to those shown. Then, we will only reduce the above mentioned trihemitone between the diatonic strings as shown, making it minor in each tetrachord comma, as we made above, and this way, in addition to the inconvenience, that is removed to the players, we will have avoided many things, that would have been quite strange to be heard; because of the transitions, that would be made from one interval to the other; that aren't heard after the temperament. So, we will adjust the trihemitone at its place just this way, by adding to the high string of each tetrachord of the above shown monochord, one string in the low, that is distant from it of a [sesquiquinta] (6/5). Then this [string] added to the above mentioned high [string], will contain the sought trihemitone, and similarly it will divide the major tone of each tetrachord in two parts, according to the reason of the interval put in the mentioned tetrachord; in such a way that between the first and second diatonic, and between the added one, and the mentioned high string, we will have the chromatic tetrachord, according to our purpose. Such string then, reduced to its proportion, by mean of the temperament, will give the diatonic monochord thickened with the chromatic strings in each tetrachord; about which monochord I will not expatiate demonstrating any more; because in the modern instruments its order is used from such a long time, that by now everybody knows it: in which order, in order that the chromatic strings would be easier distinguished from the others, he who adjusted the keyboard, the way we can see it, made the keys colored, and perhaps he made it, because he knew, that chromatic was called colored by the color, as it has been said above in the chap. 16. Nor he was happy only of thickening the above mentioned tetrachords, dividing the major tone in two parts, but he also divided the minors in two semitones, the one bigger then the other; as it can be seen in those instruments. And I think he made it, for bigger convenience of the players, so that they could express various modes and various harmonies with bigger freedom in their modulations, in the bass and in the treble. The colored strings were then signed by the practical musicians in their songs, and signed by two signs; so as the tritesynemenon by this letter [rob] round of Guidone, that they call [rob] flat, and so all those, that are consonant with this, in the bass as well as in the treble, by an octave, or a fifth, or a fourth; Then they noted the others with this sign #, that they call diesis, perhaps because they followed the opinion of Philolaus, who (as Boethius says) said, that that space, for which the [sesquiterza] (4/3) is greater then two tones, was called diesis; which space some moderns call minor semitone: because most of the times it is set, to make the interval of a semitone, as we will see elsewhere. And when they desired that that semitone would be sung somewhere in their songs, and raised from the bass to the treble, they put the [rob]: but when they descend from the treble to the bass, they put the #, as also the moderns do, when raising, and descending, by those signs, or strings, they want to put the tone. I believe that this sign # had been introduced by some, who dreamed, that the tone was, or was composed of nine commas, or that it could be divided in almost so many parts: as they pretended, that the major semitone was made of five commas, and the minor of four, and consequently, when they moved from the diatonic strings to the chromatic, the way I described; for the space of one semitone they put such sign, to indicate this interval: because they opined (as many moderns do as well) that such interval was the minor semitone, and was made of four commas; so they signed the space by four crossed inverted commas, that are the four put in that sign: as they followed the order, the number and the Pythagorean proportions of the strings, as shown above. But at what extent they are wrong, can easily be understood from what we have said and seen above, and from what Boethius says in the Chap. 15 of the Third book of the music, showing that the tone of [sesquiottava] (9/8) proportion is greater then eight, and smaller then nine commas. And in the Chap. 14 he says, that the minor semitone is greater then three commas, and smaller then four. But then if the tone is greater then eight, and smaller then nine commas, and it couldn't have any certainty of its quantity, it surely appears a big arrogance to me, that someone would affirm with determination a thing, that the Science puts in doubt, and indeterminate. Therefore if this interval cannot be named by a certain quantity, to a smaller extent could be named those, that are smaller, as the major semitone, and the minor, and the similar others.
--------------
How we can thicken the mentioned monochord with the enharmonic strings. Chap. 47
Then, wanting thicken the mentioned instrument with the enharmonic strings, so as to have, in each tetrachord, the major semitone divided in two Diesis, we will just put a string in the middle of it in such a way, that it is consonant with one of the mentioned diatonic or chromatic [strings], and we will have obtained our purpose. But before going on further, I think I have to show the Proportions of the Tetrachord, so as to know the ratio of its intervals, should one want to thicken the syntonic diatonic monochord. So it must be known, that since each enharmonic tetrachord moves from the bass to the treble by two Diesis', and one undivided ditone; as it has been said many times: we have to elect the one, having its intervals contained by proportions, that would lead to the use of the perfect harmony; nor will we have to regard those, that have been placed in many tetrachords by the antiques: as they are not apt for the generation of the perfect sweet concerted music, and have little to do with our purpose. Therefore, we have to elect those intervals that are useful; so that things are not multiplied without necessity. And it must be noted, that I say that those intervals are useful, that, when added to others, give some consonance. So we will elect first, the one, that could be elected from the above mentioned tetrachord, which is useful, and fits our purpose; then, we will add intervals, contained in proportions, such that after the above mentioned monochord will have been thickened, according to the ratios of the proportions, that I'll show soon, every string has its corresponding diatonic, or chromatic, being consonant. So, the ditone , that Ptolemy puts in his enharmonic tetrachord, shown in chap. 37, fits our purpose: because it is a consonant interval, and its true form is set between the numbers, containing the proportions, that are between the parts of the senarius; and it is in noway different by the ditone that is placed in the syntonic diatonic monochord, although it is to be considered composite in the diatonic, and having no composition in the enharmonic: as both the one and the other are contained in the [sesquiquarta] (5/4) proportion. So, this will be the acute interval of this tetrachord, and we'll have three strings, i.e. the two extremes of each diatonic or chromatic tetrachord, that are common to each genus, and the second low, that is common to each as well. After having found the fourth string, which divides the semitone of each tetrachord diatonic and chromatic in two parts, this will be the third acute [string] of the enharmonic tetrachord. Then, we will put the second enharmonic string between the first, and the second diatonic this way, making it distant from the first for a [sesquiventesimaquarta] (25/24) proportion, id est, for the space of the minor semitone, that will be the major diesis of this tetrachord, and from the second for a [supertripartiente 125] (128/125), that will be the minor diesis; and we will have this tetrachord; in which we can see the utility, given by the second low string: as
[image]
by adding it to the third string of the Hypaton chromatic tetrachord, that is the parhypate hypaton, the ditone [third] can be heard, contained in the [sesquiquarta] (5/4) proportion. But since (as I have said) the two extremes, and the third string of the mentioned tetrachord are common; then it will be enough adding to each tetrachord the mentioned string only, that could be obtained easily, by adding to the third string of each chromatic tetrachord an additional string toward the acute, being distant by a [sesquiquarta] (5/4) proportion. Then this [string], after having been proportionated in the above mentioned instruments, will be of such and so great utility; that every diatonic and chromatic string of the mentioned instruments, both toward bass and acute as well, will have a corresponding string for a ditone, and a semiditone; and this will result in such an order, from which we can understand, how much values the Art helped by the Nature, in joining, and wonderfully setting, by a beautiful, and ruled order, the chromatic strings between the diatonic, and between the ones, and the others of these, the enharmonics; that will be distinguished in the keyboards of the mentioned instruments by this: that, differently from the diatonics, and the chromatics, will be made red in color; as in the below shown instrument it can be seen. But it must be pointed out, as I have said already, that in an instrument, there those strings are put usefully and in a given order, which are put in such a way, that both toward the bass, or toward the treble, they have a corresponding string being consonant for a fifth, or a fourth, or a major third, or a minor third; as are those, that in this instrument are found. So on the contrary, those [strings] are placed without any utility, when they do not have such correspondent: so that they do not, or few, fit to the purpose of the generation of any consonance. Then, everybody will be able in the future, to make an instrument like the one I have shown; which will be convenient, and suitable to serve for the modulations, and harmonies of the mentioned genus; and this will not appear difficult to anyone: as I had it made in the year of our Lord 1548. in Venice, in order to see, how the chromatic, and enharmonic harmonies would come out; and it was an harpsichord, that is near me also, that was made by Maestro Dominico Pesarese excellent maker of such instruments; in which not only the major semitones are divided in two parts, but also all minors. And even if other [instruments] could be made with different divisions, still I believe, that
[image]
few utility could be extracted from them: as in them the strings are multiplied without any necessity; which [strings] (in addition to the shown ones) aren't suitable to express other, more delightful harmonies, then those that can be heard, because of those [strings], that are put in the shown instrument; which [harmonies] are truly diatonic, or chromatic, or enharmonic. And if anyone should believe, that other harmonies could be expressed, more then the above mentioned three; they are far wrong: because no other kind of diatonic, nor of chromatic, nor of enharmonic could be reduced (as I showed elsewhere) to its perfection, as anybody could se, by making whatever test. But since I think, that at this point the division of those genus, and their nature is well-known to every ingenious person, then I will not expatiate further, in giving them any more explanation: as most of the difficulties, that could occur, and are of some importance in this Science, can be seen demonstrated, and explicated with every diligence in our "Demostrazioni harmoniche"; then I will let the rest of the things to the judgement of the of the discreet reader, who will have got a very good practice in the handling of the numbers and of measures.In conclusion, I will say then, that this is an instrument, over which every excellent player can practice, not only in the diatonic harmonies: but also in the chromatic, and in the enharmonic: either when he could reduce them to the ancient modes, or when they could come out better for our time, and sweeter, then they were heard. And I will say also, that if one should want to add any more string to the number of the shown ones, with no doubt it would be a vain and superfluous thing: as uselessly, and inappropriately things would be multiplied, from which no utility would be drawn, and the useful, and necessary intervals, that contribute to the constitution of every kind of harmony, are already set in their proper rooms.
ITALIAN ORIGINAL TEXT
In qual modo si possa diuidere qual si voglia interuallo Musicale in due parti equali. Capitolo 24.
FARA adunque molto al proposito nostro (volendo mostrare in qual modo si possa diuidere qualunque interuallo musicale in due parti equali) la Nona del Sesto di Euclide, secondo il Campano; ouer la 13. et Problema quinto secondo Theone, che dice. Essendo date due linee rette, potemo ritrouar quella del mezo proportionale: conciosia che tanto è, come se dicesse, che Essendo dati due suoni, potemo ritrouare a questi vn mezano suono proportionale; et questo è il modo. Poniamo che nel sottoposto essempio sia accommodata alla sua proportione la consonanza Diapason, tra la chorda a b, et la c b; et sia dibisogno di ritrouare vna chorda mezana, che posta tra queste due, la diuida geometricamente in due parti equali. Allungaremo primieramente la linea a b, incominciando dal punto b verso banda destra, infino al punto d, in tal maniera, che la b d sia equale alla c b, et haueremo la a d. Fatto questo, descriueremo vn Semicircolo, il cui diametro [-94-] sia tutta la a d: dipoi tiraremo vna linea, che partendosi dal punto b, doue la detta a b si congiunse con la b d, vadi perpendicolarmente alla circonferenza del Semicircolo in punto e; et sarà la b e; et questa sarà la ricercata chorda mezana. Et per dimostrar questo, tirarò la linea a e, et la e d, et uerrà il triangolo a e d, chiamato da i Geometri Orthogonio, il quale (come per la 31. del terzo di Euclide è manifesto) è di tal natura, che hà vno angolo retto, che è l' angolo e: Onde essendo questo triangolo diuiso dalla linea e b, che casca perpendicolarmente dalla circonferenza del Semicircolo nell' angolo retto alla sua base; come si può veder nella figura, nascono etiandio due triangoli minori, l' vn maggior dell' altro; i quali sono lo a b e, et lo e b d, di specie, et di natura in tutto simili al triangolo a e d; et sono proportionati l' vno all' altro, come per la Ottaua del Sesto libro de gli Elementi di Euclide è manifesto.
[Zarlino, Le istitutioni harmoniche, 94; text: a, c, b, e, f, d, Chorda mezana proportionale. Diapason consonanza.] [ZAR58IH2_06GF.gif]
Et per il Corrolario di tal propositione, la proportione della a b alla b e, è quella istessa, che è dalla b e alla b d, secondo il nostro proposito. Facendo hora la f b equale alla b e, haueremo la diuisione equale della proposta consonanza dalla chorda f b, come si ricerca. Et chi volesse veder la proua di questa operatione, potrà diuidere la Disdiapason al mostrato modo: percioche allora conoscerà , che quella chorda mezana, che la diuiderà in due parti, sarà equalmente distante, tanto dalla estrema chorda graue, quanto dalla estrema acuta di tal consonanza, per vna Diapason, secondo 'l proposito.
Vn' altro modo di diuider qual si voglia Consonanza, ouero Interuallo musicale in due, ouero in più parti equali. Capitolo 25.
L' ALTRO modo di diuider le consonanze, in due, ouero in
quante parti si voglia, che siano equali, è non solamente
bello: ma anco più vtile del primo, per essere più vniuersale;
et fu ritrouato da Eratosthene, quando ritrouò il raddoppiamento
del Cubo, nel tempo che i Dalij (come narra Giouanni Grammatico)
erano molestati dalla pestilenza; La quale inuentione, et molte
altre insieme pose Georgio Valla Piacentino nel Quarto libro
della [-87-
[Zarlino, Le istitutioni harmoniche, 87
Porremo dipoi li Quadrati nel detto canale l' vn dopo l' altro
in tal modo; che 'l primo senza diametro sia nella parte sinistra,
et resti immobile; dipoi gli altri, che hanno li diametri, cioè
il secondo, et il terzo per ordine a banda destra, di maniera
che 'l lato destro dell' uno sia posto sopra il sinistro
dell' altro; et cosi haueremo fatto il detto Istrumento: Il
quale sarà d e f g: et sia h i k l il primo quadrato immobile
senza diametro; il secondo n o p q, il cui diametro sia n q;
et il terzo sia r s t u; del quale r u sia il diametro. Poniamo
hora che si habbia da ritrouare vna chorda mezana proportionale,
la qual diuida in due parti equali la consonanza Diapason,
contenuta dalla proportion Dupla, tra le due sottoposte chorde,
o linee a b et c b; et siano queste equali alla a b, et alla
c b poste nel capitolo precedente. Faremo primieramente il lato
destro del primo quadrato, cioè l k equale alla a b in punto m,
et sarà l m; dipoi pigliaremo il secondo quadrato, et lo
spingeremo sotto 'l primo tanto, che 'l suo diametro n q seghi
il lato k l del primo quadrato in punto m; et cosi il primo,
et il secondo quadrato resteranno immobili. Faremo poi il lato
destro del terzo quadrato, cioè u t equale alla c b in punto x;
et posto vn fillo sottilissimo in punto m, che sarà la m x del
sottoposto essempio, lo distenderemo tanto, che passi per il
punto x. Spingeremo hora il terzo quadrato tanto sotto 'l secondo,
che 'l lato p q venghi ad esser segato dal diametro r u, et dal
detto fillo in vn punto, che sarà y; et quella parte del lato
destro del secondo quadrato, la qual resterà sotto 'l fillo,
che è la q y sarà la ricercata linea, o chorda proportionale;
come nella figura si vede. Et questo è manifesto per la
demostratione precedente: imperoche la linea mezana proportionale
q y ritrouata nel Mesolabio tra la a b et la c b è equale alla
b e ritrouata nel capitolo precedente. Questo si potrebbe prouare,
se 'l si descriuesse in vna superficie piana tutte le linee fatte
nel Mesolabio, allungando primieramente per la Seconda dimanda
del primo di Euclide, la linea m x in punto z: percioche allora
haueressimo tre Triangoli continenti vno angolo retto, cioè
l m z: q y z: et u x z: da i quali si dimostrarebbe per gli
Principij et Demostrationi di Euclide, il tutto esser vero;
si come per il Secondo parer commune, et per il nono: per
la 28, et per la Seconda parte della 32. del primo: per la
seconda, per la quarta, et per la sesta del Sesto; et per la
vndecima del Quinto; le quali lasso: percioche nelle nostre
Demostrationi harmoniche hò cotal cosa diffusamente trattato.
Bastarami adunque solamente dire, che volendo ritrouar più linee
mezane, o chorde proportionali; cioè volendo diuidere in più
parti qual si voglia Interuallo Musicale, bisogna vsare il
mostrato modo. Bisogna però auertire, che per ogni linea,
o chorda che si vorrà aggiungere oltra la ritrouata, sarÃ
dibisogno di aggiungere etiandio vn altro Paralellogrammo,
o Quadrato col suo diametro, fatto di maniera, et di grandezza,
come sono li primi; facendo poi, che i lati destri di ogni
Quadrato venghino ad esser segnati in vn punto istesso da i
diametri, et dal fillo al mostrato modo.
[-96-] [Zarlino, Le istitutioni harmoniche, 96; text: MESOLABIO,
a, c, b, h, n, k, r, p, t, m, y, x, g, i, o, l, s, q, u, z, d, e, f]
[ZAR58IH2_06GF.gif]
Auertendo di por sempre il primo quadrato senza diametro,
che sia immobile; et che 'l suo lato destro sia segato dal
diametro del seguente in quel punto, che si porrà per la
lunghezza della linea proposta maggiore; et che 'l lato destro
dell' vltimo sia segato dal fillo in quella parte, che si piglia
la lunghezza della linea minore proposta, secondo 'l modo dato.
Et se la maggior linea proposta fusse più lunga, che il quadrato
posto nel Mesolabio, non si potrebbe fare alcuna cosa. E ben vero,
che pigliando la metà , di ciascuna delle due proposte, si potrÃ
hauere il proposito: perche dopo fatto il tutto, le mezane
ritrouate si potranno allungar secondo la ragione della parte
presa delle proposte linee; et cosi ogni cosa tornerà bene.
Quel che si dee osseruare nel temperare, ouero accordare gli Interualli
di ciascuno Istrumento arteficiale moderno, riducendo il numero delle
chorde del Diatonico sintono a quello del Diatono; & che tali interualli
non siano naturali, ma si bene accidentali. Cap. 42.
Et accioche il Lettore Studioso sappia, con qual ragione, & di quanta
quantità ogni interuallo ne i detti Istrumenti si venghino a temperare,
& il modo che hauerà da tenere, volendo fare la Participatione, di maniera
che non offendi il Sentimento, pigliarò hora questa fatica; & mostrarò
insieme in qual maniera le 17. chorde, poste nel Diatonico sintono, si
riduchino al numero delle Sedici contenute nel Diatono. La onde si debbe
auertire, che volendo fare tal Temperamento, o Participatione con qualche
ragione, & con qualche fondamento, fa dibisogno di diuidere il Coma,
contenuto tra le chorde R B, et M B in Sette parti equali, & distribuirle
tra li Sette interualli, contenuti nelle Otto chorde della Diapason;
accioche possiamo ridurre le due mostrate chorde, che contengono il Coma,
in vna sola. Ma si debbe fare, che gli interualli restino nella loro forma,
più che sia possibile; accioche l'Vdito non sia offeso: & che ciascuna
consonanza, si nel graue, come anco nell'acuto; & qualunque altro interuallo,
quantunque minimo sia equalmente accresciuto, o diminuto di vna certa,
& terminata quantità , in tutti gli interualli, che sono simili di proportione.
Il che tornerà molto bene, quando si farà , che ogni Diapente resti diminuta,
& imperfetta, di due Settime parti del Coma; & che la Diatessaron pigli
vno accrescimento di tanta quantitade; & è il douere: conciosia che restando
la Diapason sempre immutabile, & nella sua proportione vera, & naturale
& essendo integrata da queste due parti, quello che si leua da vna, bisogna
necessariamente dare all'altra; accioche aggiungendosi insieme, ne gli
estremi si oda la Diapason perfetta. Si farà dipoi il Ditono imperfetto di
vna settima parte, & di tanta quantità si diminuirà etiandio il Semiditono:
Percioche se queste due consonanze concorreno alla integratione della
Diapente; essendo questa diminuta di due settime parti, è necessario, che
tal diminutione si diuida tra questi due interualli: conciosia che facendo
imperfetto il Ditono di vna settima parte, & il Semiditono di altra tanto,
che sono due settime parti; queste due consonanze, che sono parti della
Diapente vengono ad esser diminute di quella quantità istessa, che è diminuto
il suo Tutto. Ma le parti del Ditono, che sono il Tuono maggiore, & il minore,
si faranno imperfette in cotal modo: si leuarà dalla prima quattro settime
parti del Coma, & si farà maggiore la seconda di tre; & cosi tra loro
verranno hauere quella imperfettione istessa, che hà il suo Tutto; cioè
saranno imperfette di vna settima parte. Si darà poi al Semituono maggiore
lo accrescimento di tre settime parti: conciosia che essendo la minor parte
del Semiditono, & il Tuono maggiore la maggior parte, tra queste due parti
si ritrouerà lo stesso mancamento, che si ritroua nel Semiditono; cioè
saranno diminute . L'Essachordo maggiore, & il minore, l'vno & l'altro
verranno a pigliare lo accrescimento di vna settima parte: imperoche l'vno
si compone della Diatessaron, & del Ditono; & l'altro medesimamente della
Diatessaron, & del Semiditono: Onde pigliando la Diatessaron accrescimento
di due parti, & diminuendosi il Ditono, & anco il Semiditono ciascuno da
per se di vna settima parte; vengono tali Essachordi ueramente a pigliare
lo accrescimento di tal quantitade. Di modo che hauendo vltimamente per
tal maniera proportionato lo Istrumento, ogni consonanza, & ogni interuallo
dal maggiore al minore; cauandone la Diapason, & il Semituono minore mostrato,
verrà ad esser fuori della sua vera proportione; non però molto lontano dalla
sua vera forma, di maniera che l'Vdito non se ne contenti. Questo adunque
bisognerà osseruare, volendo la Participatione, ouer Distributione del Coma,
in ogni nostro istrumento; accioche ogni consonanza nella sua specie venghi
ad essere equalmente accresciuta, ouer diminuta. La onde ciascun perito del
suono debbe auertire, che volendo temperare, ouero accordare gli Istrumenti
nominati, farà dibisogno di tirare, o proportionare ciascuna Diapente in tal
maniera, che li suoi estremi acuti tenghino del graue, secondo la quantitÃ
detta, ch'io son per mostrare; oueramente che li graui più si auicinino
all'acuto, secondo che nello accordare, o temperar detti istrumenti tornerÃ
più commodo. Similmente ciascuna Diatessaron, alla quale si danno le quantità ,
che si tolgono alla Diapente, si debbe accrescere in tal modo, che ogni suo
estremo acuto sia più lontano dal graue per tanta quantità , & il graue
similmente dall'acuto. Et quantunque questi interualli siano per tal maniera
hora cresciuti, & hora diminuti; non per questo l'Vdito (come hò detto)
abhorisce tale distributione: conciosia che essendo minima, & quasi
insensibile la quantità , che si leua, o aggiunge a cotali interualli;
& essendo non molto lontani dalle loro vere forme, il senso si cheta.
Ne di ciò douemo marauigliarsi: percioche all'Vdito interuiene quello,
che suole intrauenire a gli altri sentimenti, & massimamente al Vedere,
che alle volte non si accorge di vna quantità minima, per esser quasi
insensibile, si come auiene; che se'l si leua, ouero se'l si aggiunge ad
vn monte grande due, tre, ouero più pugni di grano, non può accorgersi
di tal cosa: ma si bene si accorgerebbe, quando se li leuasse, oueramente
aggiungesse vna gran parte. Ma se alcuno dicesse, che ponendosi in vso
le Consonanze, che sono fuori delle loro vere proportioni, le quali,
senza dubbio, non sono senza soauità , che i veri, & legitimi interualli
consonanti fussero questi, & non quelli, che già hò mostrato, costui
veramente sarebbe in errore: conciosia che quantunque gli interualli
già mostrati non si ritrouino essere ne i nominati istrumenti; non seguita
però, che non siano i veri, & naturali; & che non siano quelli, che producono
perfettamente in essere ogni consonanza, che è possibile da essere produtta.
Ne anco seguita, che non si possino porre in atto, & vdire: percioche si
possono vdire quando si vuole; si come etiandio non seguita, che l'huomo
non sia risibile, perche non rida sempre: perche se bene hora non ride, è
almeno atto a ridere quando vuole. Et benche ne i detti istrumenti temperati
in tal maniera, non si possino vsare le consonanze nella sua perfettione,
cioè nella loro vera, & naturale forma; è nondimeno possibile di poterle
vsare, quando le loro chorde si volesero tirare sotto la ragione delle loro
proportioni vere, & naturali. Et questo io dico, perche molte volte ne hò
fatto la esperienza sopra vno istrumento, il quale feci fabricare a questo
proposito; ancora che tal proua si possa anco fare sopra qualunque altro
istrumento; & massimamente sopra Arpichordi, o Clauocembali, che sono molto
atti a tal proposito. Et se alcuno dicesse, che quando tali istrumenti
fussero accordati perfettamente, si verrebbe a perdere alquante consonanze,
che si ritrouano essere ne gli altri istrumenti; Questo importa poco:
percioche mi basta solamente, che alcuno non possa contradire con veritÃ
a quello, ch'io hò detto di sopra, & dire che tali consonanze non si possino
porre in atto nelle loro vere forme, o proportioni: Imperoche se bene in
essi non si potesse essercitare le harmonie con quel commodo, & liberta,
che si troua ne gli istrumenti communi; non restarebbe, che in essi non si
potesse vdire ogni consonanza, & ogni harmonia nella sua vera forma. Ma se
cotali inconuenienti (dirò cosi) si trouano ne gli Istrumenti arteficiali,
nondimeno tra le Voci, come altre volte diremo, non si trouano tali rispetti:
conciosia che riducono ogni cosa nella sua perfettione, come è il douere:
essendo che la Natura, nel fare le cose, è molto superiore all'Arte: & questa
nello imitare fa ogni cosa imperfetta, & quella (rimossi gli impedimenti)
ogni cosa riduce a perfettione. In cotal modo adunque si verrà a temperare
ciascuno delli nominati istrumenti; nelli quali si farà la Distributione del
Coma in sette interualli, come hò detto; ne altramente verrebbe bene,
volendo acquistar le consonanze perfette, & le imperfette insieme, con quel
modo megliore, che si può fare; accioche ogni interuallo simile, si nel
graue, come nell'acuto venghi ad essere equalmente accresciuto, o diminuto
della sua quantità ; & non si habbia più a porre la chorda d, raddoppiata.
Et se ad alcuno paresse strano, che nella Musica occorrino simil cose;
si debbe ricordare, che non solo in questa scienza; ma in ogn'altra ancora,
in ogni arte, & in ogni altra cosa creata si ritroua grande imperfettione.
Et questo, credo io che habbia voluto Iddio Ottimo Massimo; accioche,
vedendo la imperfettione di queste cose inferiori, voltiamo lo intelletto
nostro alla contemplatione della sua Infinita Sapienza, nella quale si
ritroua ogni cosa non solamente Perfetta, ma etiandio Ottima.
--------------------------------------------------------------
Dimostratione dalla quale si può comprendere, che la mostrata Participatione,
o Distributione sia ragioneuolmente fatta; & che per altro modo non si
possa fare. Cap. 43.
VERRO' hora a dimostrare la ragione di tale Participatione: ma si de sapere,
che sono stati alcuni, che hanno hauuto parere, che l'interuallo del Coma
mostrato di sopra si douesse distribuire tra quelli due interualli, che
sono a lui più propinqui, posti nella parte acuta, & nella parte graue,
facendo di esso due parti equali, accrescendo l'vno, & l'altro interuallo
di tanta quantità , quanta è la metà di esso Coma; lassando poi gli altri
interualli nelle loro forme naturali: ma in vero a me pare, che molto
s'ingannino per molte ragioni: prima perche quelli due interualli, che
sono al Coma vicini, verrebbeno soli a participare delle parti del Coma,
& non alcuno de gli altri, & lo istrumento verrebbe ad esser proportionato
inequalmente: conciosia che si vdirebbe in lui la Diapente, & la Diatessaron
con due interualli l'vno maggiore dell'altro; dipoi, perche quelli interualli,
ne i quali si facesse questa distributione, verrebbeno ad essere dissonanti,
per la molta distanza, che hauerebbeno dalle lor forme vere; & li Tuoni,
i quali sono vicini a tal Coma, & participano di vna delle sue parti,
sarebbeno contenuti da vna proportione, che non si potrebbeno aggiungere
ne alla Diapente, ne alla Diatessaron, ne al Semiditono per formare alcuna
consonanza. Et se bene lor dicono, che la esperienza dimostra, che questi
interualli accresciuti, o diminuti per tal modo, non si partono dalla sua
propia forma di modo, che l'vdito ne patisca cosa alcuna, non altramente
di quello che farebbe, quando tal Coma non fusse in tal maniera distribuito;
questo non è vero. Onde mi penso, che costoro non habbiano mai fatto alcuna
proua di questo: conciosia che il sentimento istesso lo fa manifesto, che
sono dissonanti; & cio potrà ciascuno da se stesso prouarlo, diuidendo il
detto Coma in due parti equali, nel modo che al cap. 24. di sopra hò mostrato:
percioche aggiunte dipoi le parti, che nasceranno alli due tuoni Sesquinoni,
che li sono vicini, ciascuno potrà conoscere, che quello, ch'io hò detto,
è il vero, & che bisogna cercare di distribuire tal Coma per altra maniera,
acciò l'Vdito non sia offeso. Ma perche di sopra hò detto, che delle
Consonanze, ouero altri Interualli, alcuni si diminuiscono (facendo tale
distributione) di due, alcuni di quattro, & alcuni di vna settima parte del
detto Coma: Similmente alcuni si accrescono di vna settima parte, alcuni di
due, & alcuni di tre parti; di maniera che finalmente non solo ogni Diapente,
ogni Diatessaron, ogni Ditono, & ogni Semiditono, che sono interualli
consonanti, vengono ad essere accresciuti, o diminuti equalmente, & vengono
a restare equali si nella parte graue, come anco nel mezo, & nell'acuto
dello istrumento; ma etiandio li dissonanti, che sono il Tuono maggiore,
il minore, & il maggiore, & minor Semituono. Però tanto più questo terrò
esser vero, quanto che vn segno manifesto ne dimostra, che tal distributione
sia buona, & fatta con ogni douere: Imperoche il Semituono minore, che è
contenuto dalla proportione Super 7. partiente 128. che non si adopera nel
genere Diatonico, & è contenuto tra le chorde S B, & K B, si fa minore di
tutte le parti, cioè di tutto il Coma intero, che viene ad esser contenuto
interamente dalla proportione Sesquiottantesima; & cosi resta nella proportione
Sesquiuentesimaquarta. Onde la sua proportione resta rationale, le altre poi,
cauandone tutte le Diapason, che si contengono nella proportione Dupla,
sono irrationali, & incognite: conciosia che le parti, le quali si leuano,
o aggiungono alle quantità rationali, che sono le loro prime forme naturali,
sono irrationali, quando la diuisione del Tutto nelle parti è irrationale,
et quello che uiene, è similmente irrationale. Et si come etiandio è
irrationale quello, che nasce dalla aggiuntione, o sottratione di vna
quantità rationale da vna irrationale; cosi è irrationale quello, che viene
dalla sottratione, o aggiuntione di una proportione irrationale da vna rationale.
Ma questo non intrauiene nelle rationali: perche tutto quello che nasce,
aggiungendo, o sottraendo l'vna quantità dall'altra, è rationale. Il perche
questa distributione, che si fa aggiungendo, o leuando tal parti, non può
essere per alcuna cagione rationale; ne si può con determinati numeri a patto
alcuno denominare, o descriuere: conciosia che la diuisione del Coma in sette
parti equali non è rationale. Per mostrare adunque che tale Distributione si
conuien fare necessariamente nel detto modo, & non in altra maniera procederemo
con questo ordine. Pigliaremo prima Dodici chorde solamente del Monochordo
posto di sopra, cioè F B, E B, D B, I B, H B, G B, S B, K B, N B, R B, M B, & L B,
le quali saranno basteuoli a dimostrare il proposito; & dipoi accordaremo
perfettamente le chorde. F B & N B di maniera, che contenghino la consonanza
Diapason; le quali lassaremo immutabili, & sopra di esse daremo principio a
fare tal Distributione; Ancorache si potrebbe incominciare sopra quali chorde,
che si volesse: ma faremo questo, per seguir la maggior parte di coloro, che
accordano gli istrumenti moderni: imperoche danno principio sopra tali chorde.
Si debbe però auertire, ch'io hò detto immutabili; essendo dibisogno, che la
prima chorda sopra la quale si viene a fondare la Distributione, sia stabile;
et che ciascuna Diapason si riduca alla sua perfettione, cioè nella sua vera
forma, la quale è la proportione Dupla: percioche non patisce mutabilità ,
o variatione alcuna. Posto adunque che noi haueremo queste chorde stabili,
tra quelle chorde, che si trouano collocate nel mezo di loro, faremo la
Distributione, seruendosi però delle altre chorde, che sono poste fuori di
esse. Et per incominciare, pigliaremo la prima Diapente posta nel graue,
che sarà la F B & H B, contenuta dalla proportione Sesquialtera; senza mouere
altramente la F B, faremo la H B più graue secondo la quantità di due settime
parti di un Coma, come hò detto; preponendo primieramente, et moltiplicando
alla chorda H B il Coma, soggiungendo prima alla chorda I B il Tuono minore
contenuto nella proportione Sesquinona, & diuidendola in dieci parti; onde
prese le noue parti di essa, tra la chorda, che contenerà tal quantità , et
la H B, la quale è la chorda acuta del Tuono maggiore I B & H B, haueremo
il Coma: conciosia che se dal detto Tuono leuaremo il minore, che sarà lo
I B, & la quantità delle noue parti, senza dubbio, resterà il Coma, contenuto
dalla proportione Sesquiottantesima; il quale diuideremo in sette parti equali,
secondo il modo mostrato di sopra nel cap. 25; dipoi lassando da vn canto le
due parti più acute di esso, & pigliando solamente le cinque poste nel graue,
haueremo in un tratto con la chorda a B, accommodato alle loro proportioni
irrationali due consonanze, cioè la Diapente F B & a B, & la Diatessaron a
B & N B. Pigliaremo hora la a B, che con la M B contiene la Diapente più
acuta di due settime parti equali del detto Coma; & diuiso che haueremo il
Coma R B et M B in sette parti equali, come facemmo il primo, lassando le
quattro parti più acute, che sono le due parti, che si lassano, accioche
habbiamo la Diapente nella sua vera proportione; & due altre parti dipoi
per la sua diminutione; la chorda b B ne darà il nostro intento. A questa
chorda ritrouaremo la corrispondente nel graue in proportione dupla; accioche
possiamo vdire perfettamente la Diapason; il che haueremo fatto, quando dopo
moltiplicato, et preposto il Coma alla E B, & diuiso in sette parti equali,
pigliaremo le quattro poste nell'acuto: percioche tra c B, & essa b B haueremo
la ricercata consonanza, col mezo della chorda c B secondo il proposito:
Conciosiache essendo la E B con la M B corrispondenti per suono equale nella
consonanza Diapason; & aggiungendosi all'una, & all'altra verso il graue
quattro parti del Coma, che sono tra loro equali, ne segue, che medesimamente
gli estremi di questi aggiunti siano equali, & che rendino la consonanza Diapason:
percioche per il Secondo, & per Terzo Commune parere del lib. 1. de gli Elementi
di Euclide, Se a cose Equali si aggiunge, ouero da esse si leua cose Equali,
quello che viene è similmente Equale. Haueremo etiandio tra c B & a B vna
Diatessaron accresciuta di due parti del Coma, che sarà equale in proportione
alla a B & N B. Faremo hora la chorda G B corrispondente in proportione
Sesquialtera alla c B, soggiungendo alla G B il Coma, et diuidendolo secondo
il modo dato; dipoi lassando le quattro parti poste nell'acuto, et le due,
che segueno verso il graue; tra la c B et la d B haueremo vn, altra Diapente
diminuta di due parti di vn Coma; et tra la d B & la b B vn'altra Diatessaron
accresciuta di tanta quantità . Seguono dipoi la d B & la L B, che contengono
la Diapente diminuta di vna settima parte; onde volendo la diminuire di vn
'altra parte; accioche si ritroui con le altre equale in proportione;
preponeremo alla LB il Coma, diuiso come gli altri in sette interualli,
& lassato il più acuto, prenderemo solamente li Sei posti nel graue; & dalla
e B haueremo il proposito. A questa ritrouaremo la corrispondente in
proportione Dupla, in questo modo; diuideremo il Coma preposto alla DB
in sette parti, dipoi presa la parte più acuta, haueremo la f B, che con
la detta e B ne darà la consonanza Diapason nella sua forma naturale,
et vn'altra Diatessaron equale in proportione con le altre, che sarÃ
la f B & d B, nella sua forma accidentale. Tra la f B & la K B dipoi
verrà ad essere vna Diapente medesimamente nella sua forma accidentale,
più acuta di vna di dette parti; per il che volendola ridurre alla sua
proportione, preponeremo alla K B il Coma diuiso al modo dato; & lassando
la parte piu acuta per il superfluo; & le due parti seguenti per la
diminutione, col mezo della chorda g B, non solo haueremo la vera
proportione accidentale della Diapente; ma etiandio quella della Diatessaron,
contenuta tra la g B, & la e B: Resta hora a ridurre alla sua proportione
la Diapente I B, & N B, & la Diatessaron F B, & I B; onde soggiungeremo alla
I B il Coma, il quale, dopo che sarà diuiso in sette parti, & prese che noi
haueremo le due settime parti piu graui, col mezo della chorda h B, ne darÃ
la proportione di dette consonanze; cioè haueremo accresciuta la Diatessaron
posta nel graue di tante parti, & fatta minore la Diapente
--------------------------------------------------------------------------------
[DIAGRAM:]
DISTRIBVTIONE DEL COMA TRA GLI INTERVALLI DEL MOSTRATO MONOCHORDO.
F Tuo. mag. E Tuo. mino. D Sem. mag. I Tuo. maggio. H Tuo. mi. G Semit. mag.
S Semit. mino. K Sem. mag. N Tuo. mi. R co. M Tuo. mino. L B Tuono. c Tuono.
f Semi. mag. h Tuono. a Tuono. d Se. mag. i Se. mi. g Semi. mag. Tuono.
b Tuono. e C D E F G a b y c d e Sesqui 24. Diapente. Diapente. Diapente.
Diapente. Diapente. Diapente. Diapason. Diapason. Diapason.
--------------------------------------------------------------------------------
posta in acuto di tanta quantità . Hora per dare la sua proportione alla S B,
che con la h B si ritroua esser distante per vna Diatessaron, diminuta di
due parti; soggiungeremo alla S B il Coma, & dipoi che sarà diuiso pigliaremo
le quattro parti più graui in punto i; & tra i B, & h, B haueremo fatto equale
la detta Diatessaron alle altre in proportione. Per tal modo adunque haueremo
accresciuto, o diminuto equalmente, non solo ogni Consonanza nella sua specie;
ma ogn'altro Interuallo, che tra le dette chorde era contenuto; & di Dodici
chorde che erano prima, le haueremo ridutte al numero di Vndici, corrispondenti
al numero delle chorde Pithagorice, poste di sopra nel cap. 28; le quali
potremo descriuere commodamente con le lettere di Guidone, senza raddoppiare
altramente la d. Et quello ch'io hò detto disopra intorno al Semituono minore
si vede essere verificato: conciosiache ritrouandosi nella sua proportione
tra le chorde S B & K B, & restando diminuto nel graue (come si vede nella
dimostratione) delle quattro parti del Coma, contenute tra la S B & la i B;
& nell'acuto di tre parti, contenute tra g B & K B; se noi aggiungeremo queste
tre parti alle quattro prime, non è dubbio, che arriueranno al numero di Sette,
& faranno tutto il Coma. Ma perche (come altroue hò detto) il Coma è contenuto
dalla proportione Sesquiottantesima; però se dalla Super 7 partiente 128,
che era la prima forma del Semituono minore, che è rationale, leuaremo la
Sesquiottantesima, la quale etiandio è rationale; il rimanente sarà la proportione
Sesquiuentesimaquarta rationale, la quale è la forma rationale di tal Semituono.
Potemo hora vedere in qual maniera le parti del Coma si venghino a distribuire,
con vna certa equalità , in ogni Consonanza, et in ogni Interuallo. Per la qual
cosa potemo tenere per certo, che questo modo tanto più sia migliore, & più vero,
quanto vedemo, che ogni consonanza, & ogni interuallo, si nel graue, come nel
mezo, & nel fine, è accresciuto, o diminuto di vna istessa quantità , secondo
che ricerca la sua proportione: Ne si vede per modo alcuno, che l'vno sia
maggior dell'altro, o minore: ne si scorge, che in essa sia alcuno auanzo
quantunque minimo, di alcuna parte del detto Coma: Imperoche quando si ritrouasse
alcuna di queste cose, sarebbe segno manifesto, che tal Distributione non fusse
fatta co i debiti modi. Onde concludo, che quando si uolesse tentare di fare
tal Distributione altramente, che tal fatica sarebbe vana, & senza frutto;
come la esperienza sempre lo farà manifesto. Per la qual cosa non si potendo
fare cotal cosa in altra maniera, che torni bene ne i sopradetti istrumenti;
seguita che tal participatione, o Distributione sia fatta perfettamente,
con li debiti mezi, et senza alcuno errore.
updated:
2003.03.10 -- page created
2003.03.25 -- added cap. 46
