major-3rd / major third / maj3 / M3
A diatonic interval composed of 2 tones (i.e., "whole-tones"), whose diatonic pitch distance always traverses 3 letter-names inclusively (which may or may not involve a change of accidental), and which is approximately 400 cents (give or take about 50). For example, in the key of C-major ("t" = tone, "s" = diatonic-semitone) :
M2 M2 m2 M2 M2 M2 m2
t t s t t t s
C D E F G A B C = C-major diatonic scale
| |
--- major-3rd----
major-3rd = 2t + 0s
= 2(M2)
Some examples of major-3rds which include accidentals:
- Abb : Cb
- Ab : C
- A : C#
- A# : Cx
- etc.
The standard 12edo major-3rd is the one of 400 cents. Some typical JI or rational values are given below in John Chalmers's definition.
Successively closer small-integer rational approximations of the 12-edo major-3rd are:
ratio ~cents 14/11 417.5079641 5/4 386.3137139 19/15 409.2443014 (good approximation of Pythagorean 3rd) 24/19 404.4419847 29/23 401.3028469 34/27 399.0904069 63/50 400.1084805 (only ~1/9 cent wider than 2(4/12))
Other 'major 3rds' can be defined mathematically by irrational numbers, generally in the context of some form of temperament.
Examples of 'major 3rds' in some common meantone tunings:
meantone adjustment of 81/64 "flavor" --- [pythagorean 'major 3rd'] --- ----- 2,3,5-monzo ----- ~ cents 1/11-comma ((3/2)4) / (22) / ((81/80)(4*1/11)) = [-50/11 28/11, 4/11 > = 399.9995345 1/6-comma ((3/2)4) / (22) / ((81/80)(4*1/6)) = [-10/3 4/3 , 2/3 > = 393.4824771 1/5-comma ((3/2)4) / (22) / ((81/80)(4*1/5)) = [-14/5 4/5 , 4/5 > = 390.6149718 3/14-comma ((3/2)4) / (22) / ((81/80)(4*3/14)) = [-18/7 4/7 , 6/7 > = 389.386041 2/9-comma ((3/2)4) / (22) / ((81/80)(4*2/9)) = [-22/9 4/9 , 8/9 > = 388.7033016 1/4-comma ((3/2)4) / (22) / ((81/80)(4*1/4)) = [ -2 0 , 1 > = 386.3137139 7/26-comma ((3/2)4) / (22) / ((81/80)(4*7/26)) = [-22/13 -4/13, 14/13 > = 384.6593839 5/18-comma ((3/2)4) / (22) / ((81/80)(4*5/18)) = [-14/9 -4/9 , 10/9 > = 383.9241261 2/7-comma ((3/2)4) / (22) / ((81/80)(4*2/7)) = [-10/7 -4/7 , 8/7 > = 383.2413868 1/3-comma ((3/2)4) / (22) / ((81/80)(4*1/3)) = [ 2/3 -4/3 , 4/3 > = 379.1449507
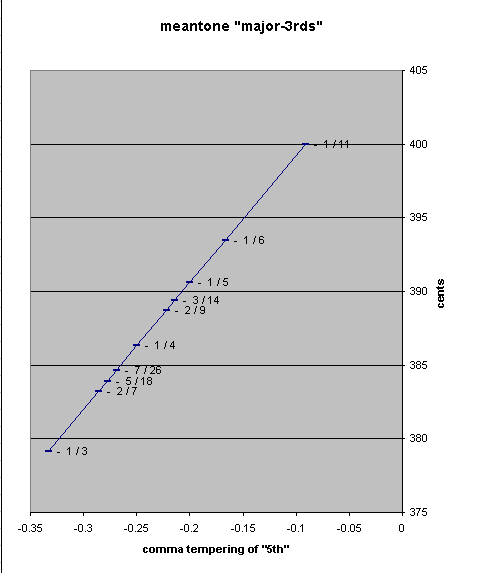
Note the frequent occurence of '4' in the numerators of the rational exponents of the monzos: this is a result of the place of the Pythagorean 'major 3rd' as the fourth member in the chain of 5ths, and the implied pythagorean ratio (2-6*)34 for the fourth member in the meantone chain.
Also note that 1/4-comma meantone gives a major-3rd with the exact JI 5:4 ratio, which is made obvious by the fact that all of the exponents in its monzo are integers.
The golden meantone "major-3rd" has the ratio 2[ (10 - 4Φ) / 11 ], where Φ = (1 + 51/2) / 2, and is ~384.8578958 cents.
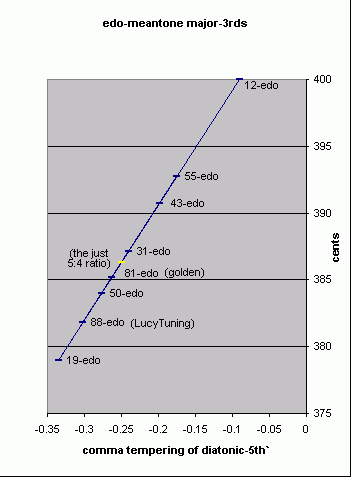
Examples of 'major 3rds' in some common equal temperaments:
| EDO | '3rd' | cents | |
| 12 | 24/12 | 400 | |
| 13 | 24/13 | ~369 | |
| 15 | 25/15 | 400 | |
| 16 | 25/16 | 375 | |
| 17 | 26/17 | ~424 | (note that 17-EDO has nothing that resembles the JI major-3rd of 5/4 ratio; also note the neutral-3rd of 2(5/17) = ~353 cents) |
| 19 | 26/19 | ~379 | |
| 22 | 27/22 | ~382 | |
| 24 | 28/24 | 400 | (also note the 'neutral 3rd' of 2(7/24) = 350 cents) |
| 31 | 210/31 | ~387 | |
| 41 | 213/41 | ~380 | (also note the pseudo-Pythagorean '3rd' of 2(14/41) = ~410 cents) |
| 43 | 214/43 | ~391 | |
| 50 | 216/50 | 384 | (also note the pseudo-Pythagorean '3rd' of 2(17/50) = 408 cents) |
| 53 | 217/53 | ~385 | (also note the pseudo-Pythagorean '3rd' of 2(18/53) = ~407.5 cents) |
| 55 | 218/55 | ~393 | |
| 72 | 223/72 | 383 1/3 |
(Note that the cents values of some ET pitches are exact.)
Below is a pitch-height graph of the size of the major-3rd in various EDO-meantone tunings:
An interval approximating 400 cents. Major thirds include the 5/4 (386¢) of Just Intonation, the Pythagorean Ditone of 81/64 (408¢), and more complex intervals such as 19/15 (409¢) and the Skhismic Diminished Fourth, 8192/6561 (384¢) of extended Pythagorean tuning.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
