consistency / consistent
An equal temperament with an integer number of notes per octave is consistent with JI through some odd limit if a complete chord of that limit is constructed in that equal temperament in the same way no matter which intervals are approximated.
If for all odd integers a, b, c such that 1 <= a < b < c <= n, the ET's best approximation of b / a plus the ET's best approximation of c / b equals the ET's best approximation of c / a, then the ET is consistent in the n-limit.
For example, the smallest ETs consistent in the 11, 13, 15, and 17-limits are 22, 26, 29, and 58-tET, respectively.
Consistency may be defined for non-octave equal temperaments but then even as well as odd numbers must be considered, and the consistency will be through an "integer limit" rather than an odd limit.
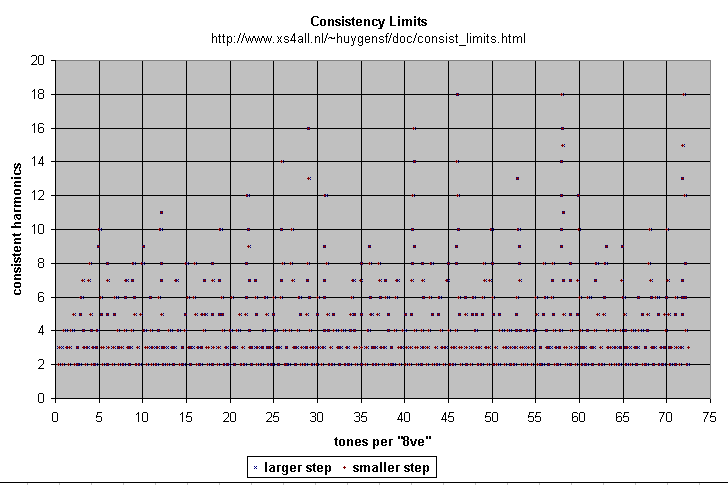
The data for case are tabulated at http://www.xs4all.nl/~huygensf/doc/consist_limits.html and http://www.xs4all.nl/~huygensf/doc/cons_limit_bounds.html. The ordinary, odd-limit consistency of an integer ET can be read from this table as well: it is the largest odd number not exceeding the integer limit.
Date: Fri, 17 Jul 1998. Subject: Equal Temperaments Here is a table showing the simplest equal temperaments with consistent representations of all just intervals through the m-limit _and_ unique representations of all just intervals through the n-limit (these are odd limits): m- 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 n | 3 3 3 5 5 22 26 29 58 80 94 94 282 282 282 311 311 311 5 9 9 12 22 26 29 58 80 94 94 282 282 282 311 311 311 7 27 27 31 41 41 58 80 94 94 282 282 282 311 311 311 9 41 41 41 41 58 80 94 94 282 282 282 311 311 311 11 58 58 58 58 80 94 94 282 282 282 311 311 311 13 87 87 94 94 94 94 282 282 282 311 311 311 15 111 111 111 111 282 282 282 282 311 311 311 17 149 217 217 282 282 282 282 311 311 311 19 217 217 282 282 282 282 311 311 311 21 282 282 282 282 282 311 311 311 23 282 282 282 282 311 311 311 25 388 388 388 388 388 388 27 388 388 388 388 388 This table cannot be extended without going beyond 650-tET. Notice that 58 is encountered in any progression from lower to higher limits. 282 is also, but that's more a curiosity than a musically important result. 7, 19, 46, 53, and 72 are conspicuous by their absence: there are simpler ETs that can "do" what they "do", just not always as accurately; namely, 3, 12, 41, 41, and 58 respectively. (Of course there can be other reasons besides accuracy to use 7, 19, 46, 53, or 72.)
The data for ETs thru 73 are plotted on the following chart:
See Patrick Ozzard-Low, 21st Century Orchestral Instruments for a more in-depth exploration of consistency.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
