kleisma
(Greek: "lock", "lid"; plural: kleismata)
The kleisma is a small interval composed of 6 major thirds up and 5 fifths down [= 3-556].
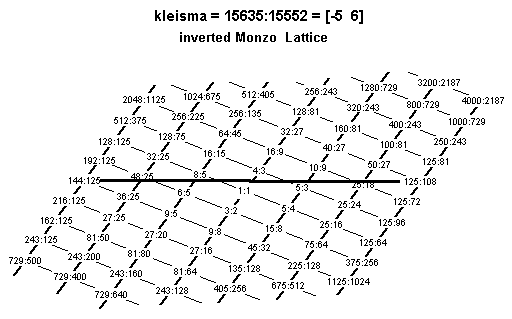
Its ratio is 15625/15552 [= 0.08 Semitones = ~8.10728 cents]. The term was introduced by Shohé Tanaka in 1890.
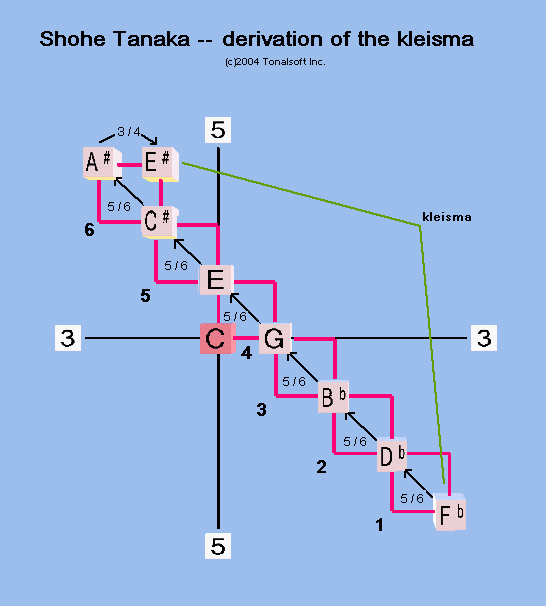
Tanaka described the kleisma thus:
Fb:A#= 4 * (5/6)^6 E#:A# = 3:4 E#:Fb = [ 4 * (5/6)^6 ] * 3/4 = 15625/15552 = 214/213 (approximately) [after Tanaka 1890, p 9-10]
The calculation is made easy with vector addition:
2,3,5-monzo ratio ~cents [ 2 0, 0> 4 1200 * 2 + [-1 -1, 1> * 6 * (5/6)^6 + -315.641287 * 6 + [-2 1, 0> * 3/4 + -498.0449991 ---------------- ---------- ------------------- [-6 -5, 6> 15625/15552 8.107278862
and is shown below on a 3,5-prime-space lattice:
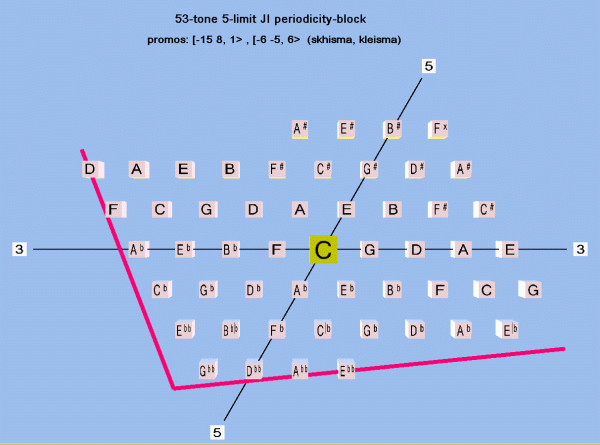
The kleisma's importance in Tanaka's tuning system lay not in any explicit use as a musical interval (i.e., harmonic or melodic), but rather, in the fact that it is treated as a unison-vector: together with the skhisma, it is one of the promos which defines a 53-tone periodicity-block ("periodic parallelogram" was Tanaka's term, possibly the earliest recognition of the concept) which is audibly indistinguishable from 5-limit just intonation, and which is nearly identical to pythagorean tuning.
Below is one lattice of a 53-tone periodicity-block derived from these two promos ... it differs slightly from Tanaka's actual diagram, in that some of this pitches were a kleisma higher.
Below is Tanaka's actual diagram. The central periodicity-block is clearly marked. Other replications of the "periodic parallelogram" are marked with various combinations of S and K to represent the transposition of the "periodic parallelogram" by skhismata and kleismata.
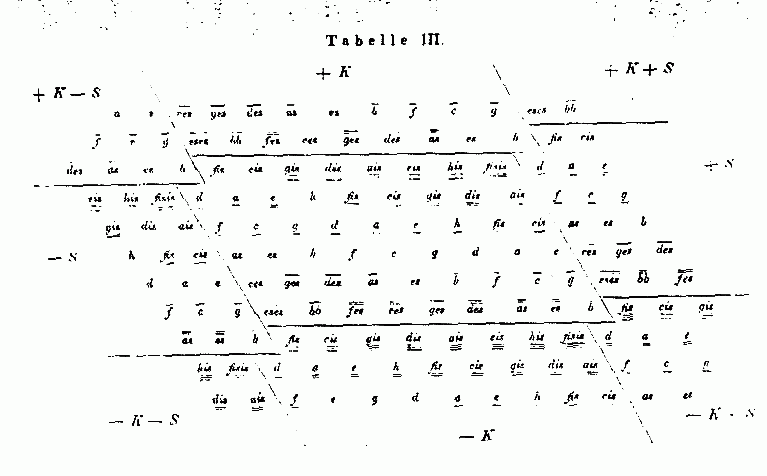
See the 53et bingo-card for more.
The approximate ratio of 214/213 has a small error of ~1/641 cent from the actual kleisma:
2,3,5,71,107-monzo ratio ~cents [ 1 -1 0 -1 1> 214/213 8.108839410 - [-6 -5 6 0 0> ÷ 15625/15552 - 8.107278862 ------------------ ---------------- ------------------- [ 7 4 -6 -1 1> 1109376/1109375 0.001560548
septimal kleisma
Another interval that has become known as a kleisma (and in fact is now the one most commonly referred as such) is the one which forms the difference between the 5-limit "augmented 6th" and the harmonic "7th":
interval ratio 2,3,5,7-monzo ~cents
5-limit "augmented-6th" 225:128 [-7 2, 2 0> 976.5374295
- "harmonic-7th" 7:4 [-2 0, 0 1> 968.8259065
-------------------------- ------- ----------- ------------
septimal-kleisma 225:224 [-5 2, 2 -1> 7.711522991
Fokker often invoked the septimal-kleisma in precisely the way i describe here -- to make singers become familiar with the 5-limit JI "augmented-6th", then have them use it as a "target pitch" when he notates a harmonic-7th in his compositions. (This was at least as early as his 1949 English book on singing JI.)
Reference
Tanaka, Shohé. 1890.
"Studien im Gebiete der reinen Stimmung"
Vierteljahrsschrift für Musikwissenschaft vol. 6 no. 1,
Friedrich Chrysander, Philipp Spitta, Guido Adler (eds.),
Breitkopf und Härtel, Leipzig, pp. 1-90.
English translation of pages 8 to 18 by Daniel J. Wolf,
"Studies in the Realm of Just Intonation",
Xenharmonikôn vol. 16, autumn 1995, pp. 118-125.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
