constant structure
A tuning system where each interval occurs always subtended by the same number of steps. (THAT IS ALL, NO OTHER RESTRICTIONS)
A list of integers representing the cardinalities of nested MOS's is a Constant Structure of all scales that can support the entire nest. The larger the numbers, and the more of them, the fewer the number of scales in the Constant Structure (tho the number of scales is always infinite if you assume infinite tuning precision).
This was my stab at Lumma-CS, which we now know is not CS. It is a concept I got from Erv, tho; I wonder if he has a name for it?
...strict propriety does guarantee CS!
Any periodicity block where the unison vectors are smaller than the smallest steps will be CS [constant structure].
[Kraig Grady:]Here's one:
I guess i would need an example of a Periodic block that was not a constant structure.
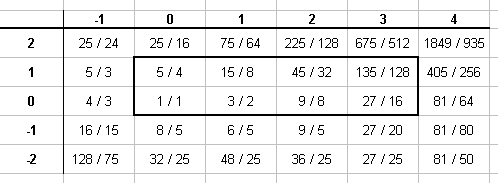
1/1 135/128 9/8 5/4 45/32 3/2 27/16 15/8
Below is a lattice-diagram of Carl's periodicity-block:
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
