A whole family of related scales/tunings derived from an optimal generator called the miracle generator or secor.
miracle is an acronym standing for
M ultitudes of I nteger R atios A pproximated C onsistently, L inearly and E venly.
The entire cycle of this generator produces 72-EDO or a very close approximation to it. Important subsets are the studloco scale (miracle-41), the (blackjack) scale (miracle-21), and most significant of all, the canasta scale (miracle-31).
In April 2001 Dave Keenan calculated "optimal" generators using several different methods. In one example, Paul Erlich illustrated the calculus involved in the "unweighted" root-mean-square 9-(odd)-limit optimizaton method in Yahoo Tuning message 22626 (Sun May 13, 2001 6:41 am). One set of optimal generators is approximately 116.7 cents, nearly identical to 7 degrees of 72-EDO, or 7/72 of an "octave". This interval has been named the secor, after the original discoverer of the family of tunings based on this generator.
In late June 2001 it became evident to tuning list subscribers that George Secor actually has precedence as the originator of the miracle temperament (though not any of the miracle MOS scales). See A New Look at the Partch Monophonic Fabric, originally published in Xenharmonikôn 3. Secor identifies his generator as 116.69 cents, but Dave Keenan found that the generator with the properties Secor mentioned is actually 116.71 cents.
As indicated by its full name, the miracle scale contains very close approximations to a very large number of consonant just-intonation harmonic structures - specifically, a lot of 7-limit tetrads and 11-limit hexads, and also exhibits a number of other interesting properties examined by theorists in regard to size of intervallic relationships (i.e., MOS, maximal evenness, etc.)
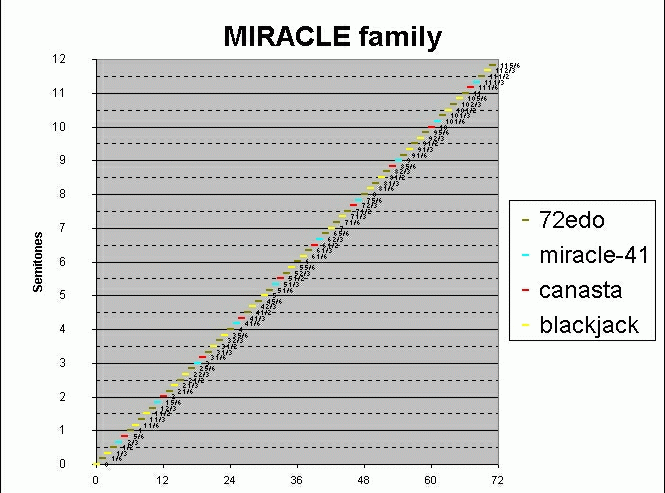
Here is a graph showing how the miracle family grows from the 21-note blackjack, thru the 31-note canasta, the miracle-41, and the full 72-EDO superset. Note that there are many other intermediary stages which were left out.
Starting at the 0th degree of 72-EDO and adding 10 pitches on either side of it 7/72 of an "octave" apart, then "octave"-reducing them, yields the blackjack cycle shown in yellow.
Adding another 5 pitches on either side of the blackjack cycle yields the extra canasta pitches shown in red. Canasta also includes all the yellow blackjack pitches.
Adding another 5 more pitches on either side of the canasta cycle yields the extra miracle-41 pitches shown in blue. Studloco (miracle-41) also includes all the yellow blackjack pitches and all the red canasta pitches.
After adding another 15 pitches to either side of the studloco (miracle-41) cycle, the 16th note on either side gives the same pitch, thus closing the cycle at 72. These extra pitches needed to complete the 72-EDO scale are shown in green.
Using more colors, two smaller MOSs, with 10 and 11 notes, could also have been shown.
Shown below is the actual derivation of the cycles by steps of the 7/72-"octave" generator in either direction from the 0th degree.
Note that every 6th step in the cycle is a "perfect 5th" in the "cycle of 5ths". Thus, the miracle scales can be thought of as:
I have notated the accidentals of this cycle to conform to the pythagorean origin of the standard notation, with the exception that I made a break between Db and F# in every case, to use a minimum number of symbols. Each "cycle of 5ths" is offset one space to the right. This diagram shows how 72-EDO can be thought of as 6 chains of "5ths".
72-EDO notation legend:
glyph cents adjustment from 12-EDO
^ + 50
> + 33 & 1/3
+ + 16 & 2/3
0
- - 16 & 2/3
< - 33 & 1/3
72-EDO ASCII 72-EDO
degree Semitones notation scale
36 6 F#
29 4 5/6 F-
22 3 2/3 E<
15 2 1/2 D^
8 1 1/3 C#>
1 1/6 C+
66 11 B
59 9 5/6 Bb-
52 8 2/3 A<
45 7 1/2 G^
38 6 1/3 F#>
31 5 1/6 F+
24 4 E
17 2 5/6 Eb-
10 1 2/3 D<
3 1/2 C^
68 11 1/3 B> ---------- studloco
61 10 1/6 Bb+ |
54 9 A |
47 7 5/6 Ab- |
40 6 2/3 G< |
33 5 1/2 F^ -------- canasta |
26 4 1/3 E> | |
19 3 1/6 Eb+ | |
12 2 D | |
5 5/6 Db- | |
70 11 2/3 C< --- blackjack | |
63 10 1/2 Bb^ | | |
56 9 1/3 A> | | |
49 8 1/6 Ab+ | | |
42 7 G | | |
35 5 5/6 F#- | | |
28 4 2/3 F< | | |
21 3 1/2 Eb^ | | |
14 2 1/3 D> | | |
7 1 1/6 Db+ | | |
0 0 C -- (origin) | | |
65 10 5/6 B- | | |
58 9 2/3 Bb< | | |
51 8 1/2 Ab^ | | |
44 7 1/3 G> | | |
37 6 1/6 F#+ | | |
30 5 F | | |
23 3 5/6 E- | | |
16 2 2/3 Eb< | | |
9 1 1/2 Db^ | | |
2 1/3 C> --- blackjack | |
67 11 1/6 B+ | |
60 10 Bb | |
53 8 5/6 A- | |
46 7 2/3 Ab< | |
39 6 1/2 F#^ -------- canasta |
32 5 1/3 F> |
25 4 1/6 E+ |
18 3 Eb |
11 1 5/6 D- |
4 2/3 Db< ---------- studloco
69 11 1/2 B^
62 10 1/3 Bb>
55 9 1/6 A+
48 8 Ab
41 6 5/6 G-
34 5 2/3 F#<
27 4 1/2 E^
20 3 1/3 Eb>
13 2 1/6 D+
6 1 Db
71 11 5/6 C-
64 10 2/3 B<
57 9 1/2 A^
50 8 1/3 Ab>
43 7 1/6 G+
36 6 Gb
Here's an explanation of the generation process which I posted in Yahoo tuning-math message 271 (Thu Jun 21, 2001 6:20 am), with graphs for illustration:
If you think of using the 2(7/72) generator to create extended (i.e., >12) scales in the same way that you can use a tempered (i.e., narrowed) meantone "5th" or the wider-than-12-edo pythagorean "5th" to create >12 "extended" cycles, I think that will help make the whole process clearer.
The meantone and pythagorean "5ths" don't close the cycle at the 13th note, because the 1st and 13th are separated by a small interval which is exactly or approximately one of the commas. (For an illustration, see "Pythagorean comma".)
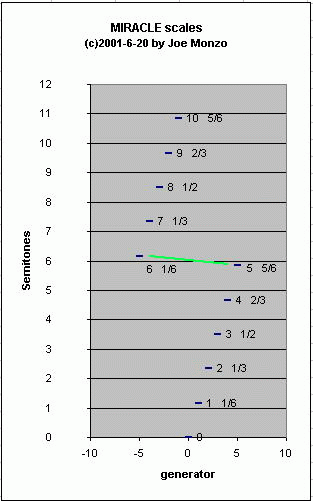
Similarly, if you call your origin 0 and create an 11-tone miracle scale, the notes at either end (-5 and +5 generators away from the origin) will be separated by 2(2/72), or 33&1/3 cents. This is a bit bigger than a "comma", but the process is the same: the resulting 2(2/72) is audibly much smaller than the 2(7/72) which occurs between all the other notes of the scale, thus (depending on musical context, of course) these two pitches are more likely to be interpreted as variant instances of the same pitch-class, rather than as two distinct scale-members.
This is shown by the green line in the graph below, and explains why Graham Breed's decimal notation works so well to describe the basic cardinality of these tunings.
By continuing to extend the cycle beyond these 11 notes, you get pairs of pitches all separated by 2(2/72), which can be seen in the graph below. This is exactly why the Blackjack scale has L=5 s=2 (in terms of 72-edo degrees).
By the time you reach a cycle bounded by -15 and +15 generators, you've filled out the "octave" pitch-space pretty evenly, hence the Canasta scale.
Extending it to one more note on either side would give a pitch separated from the one on the other end by only 2(1/72), or 16&2/3 cents (= a 1/12-tone). This is illustrated by the red line on the graph below.
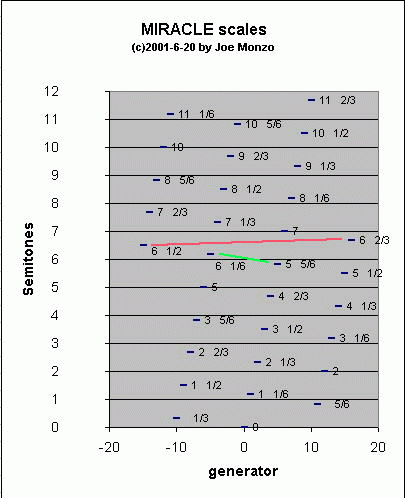
So beyond this point, all miracle scales above cardinality 31 will have pairs of pitches separated by *that* interval.
Then finally the 72nd generator closes the cycle... in other words, at that point the separation of pitches on either end finally reduces to 2(0/72), which is a unison.
Here is the mapping of the basic prime intervals in 72-EDO miracle:
7/72-EDO mapping
prime (period, gen) dec ~cents error ~ % error
2 (1, 0) 0 0 0
3 (1, + 6) 6 -1.955000865 -0.102789018
5 (3, - 7) 3^ -2.980380532 -0.106965002
7 (3, - 2) 8^ -2.159239802 -0.064094728
11 (2, +15) 5v -1.317942365 -0.031747565
(For a detailed explanation of this type of matrix notation, see Graham Breed's matrix webpage.)
Notice this tetrad in roughly the center of one of Graham's decimal lattices (showing miracle temperaments on various-limit lattice diagrams), and compare to the first 4 rows of the "prime" and "dec" column of the table above. (The absence of prime-factor 11 shows that this is a 7-limit lattice, as Graham states.)
(Thanks to Paul Erlich and Dave Keenan for corrections on historical info.)
All miracle tunings temper out the following 7-limit commas:
[ 1 0 3] 1029:1024 - [ 2 2 -1] 225:224 ------------ [-1 -2 4] 2401:2400
and also the 5-limit ampersand's comma [7 6 0].
| family name: | miracle |
| period: | octave |
| generator: | secor, the neutral semitone |
| name: | miracle, ampersand, 31&41 |
| comma: | |-25 7 6> |
| mapping: | [<1 1 3|, <0 6 -7|] |
| poptimal generator: | 41/422 |
| TOP period: | 1200.631014 mapping: 116.720642 |
| MOS: | 10, 11, 21, 31, 41, 72, 103, 175 |
| name: | miracle, 31&41 |
| wedgie: | <<6 -7 -2 -25 -20 15|| |
| mapping: | [<1 1 3 3|, <0 6 -7 -2|] |
| 7-limit poptimal generator: | 17/175 |
| 9-limit poptimal generator: | 32/329 |
| TOP period: | 1200.631014 mapping: 116.720642 |
| TM basis: | {225/224, 1029/1024} |
| MOS: | 10, 11, 21, 31, 41, 72 |
| name: | miracle, 31&41 |
| wedgie: | <<6 -7 -2 15 -25 -20 3 15 59 49|| |
| mapping: | [<1 1 3 3 2|, <0 6 -7 -2 15|] |
| poptimal generator: | 39/401 |
| TOP period: | 1200.631014 mapping: 116.720642 |
| TM basis: | {225/224, 243/242, 385/384} |
| MOS: | 10, 11, 21, 31, 41, 72, 113, 185 |
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.