Philolaus
The work of the ancient Greek music-theorist Philolaus (c.400s BC) surivives only in two brief commentaries by Boethius in Book 3 (3.5 and 3.8) of his treatise, and in one other commentary by Nicomachus. (The quotes from Boethius are reproduced below, in the original Latin and in English.)
Boethius 3.5 discusses Philolaus's measurements of ratios.
Philolaus specified that the diesis (by which he meant the diatonic semitone, later also called limma) has the ratio 256:243, and noted that the difference between those numbers is 13.
Philolaus also specified that the tone (in the sense of whole-tone) has the ratio 27:24, which reduces to 9:8. His reason for using 27:24 is that 27 is the cube of 3, which Boethius calls "the first odd number ... [which] was highly revered among the Pythagoreans".
Philolaus (or Boethius?) then notes that 243:216 is also a ratio for the whole-tone, as it too reduces to 9:8, and notes that the difference between these two terms is 27.
Since, in pythagorean tuning, the whole-tone is composed of two different-sized semitones (the smaller diatonic [limma] and the larger chromatic [apotome]), Philolaus splits this 27-unit difference into 14 + 13.
Neither Philolaus nor Boethius specify whether the 14 units are to be added to 216 or subtracted from 243 -- the two procedures produce different results.
Adding 14 to 216 gives us:
string length ratio 2,3,5,23-monzo ~cents
216
> 115:108 [ -2,-3, 1, 1 > 108.7230585
230
> 243:230 [ -1, 5,-1,-1 > 95.18694319
243
Subtracting 14 from 243 gives us:
string length ratio 2,3,229-monzo ~cents
216
> 229:216 [ -3,-3, 1 > 101.1795431
229
> 243:229 [ 0, 5,-1 > 102.7304586
243
The former result certainly resembles the regular pythagorean division (~113.7 and ~90.2 cents -- see apotome for example) much more closely than the latter, so that is what we may assume Philolaus had in mind. (There is also good reason to assume that the Greeks always thought of having the larger intervals on top.)
Philolaus makes much ado about the fact that the difference between these differences (14 and 13) is 1 ("unity"), and he equates the "comma", which is the difference in pitch-size between the apotome and limma (which he calls diesis), to 1. He says that the tone is thus made up of 27 of these "unities", implying that 27 of these arithmetical "commas" equal a tone. Calculating the true value of this comma, we get:
ratio 2,3,5,23-monzo ~cents
115:108 [ -2,-3, 1, 1 > 108.7230585 Philolaus's apotome
- 243:230 - [ -1, 5,-1,-1 > - 95.18694319 Philolaus's diesis [limma]
------------- ----------------- --------------
13225:13122 [ -1,-8, 2, 2 > 13.53611534 Philolaus's arithmetical comma
The pythagorean whole-tone of 9:8 ratio (= ~203.9 cents) is composed of almost exactly 15 of these "commas"; thus, we see that Philolaus's mathematical procedure is quite erroneous. Because our perception of pitch is logarithmic, it is incorrect to assume that an arithmetical difference between terms of a ratio always represents the same pitch size -- in fact this is not at all true.
(Despite his erudition, Boethius himself commits the same error with regard to his explanation that the tone is larger than 8 commas but smaller than 9.)
In fact, Philolaus himself later defines the comma as the difference between a tone and 2 of his dieses [limmata] (see below), which is the traditional definition of the pythagorean-comma.
In any case, if Philolaus actually did construct a monochord demonstrating these ratios (which he probably did), it was almost certainly used only for demonstration purposes, for if he tried to use an arithmetical difference of 27 between any other whole-tones in his tuning system, he would not get a 9:8 ratio.
In Book 3.8, Boethius describes Philolaus's method of dividing small intervals. This method leads to slightly different results from those obtained by his arithmetical string-length method.
-- 2,3-monzo --
2 3 ~cents
schisma [ -19/2 6 > 11.73000519
comma [ -19 12 > 23.46001038
diaschisma [ 4 -5/2 > 45.11249784
diesis [ 8 -5 > 90.22499567
integral 1/2-tone [ -3/2 1 > 101.9550009
apotome [ -11 7 > 113.6850061
tone [ -3 2 > 203.9100017
4th [ 2 -1 > 498.0449991
Ancient Greek music-theory reckoned scales downward, the opposite of the way we do today. It never used an interval smaller than a 9:8 whole-tone as the top interval of a tetrachord, and the lowest part of the tetrachord was always a semitone divided approximately in half into two quarter-tones. It was the middle section of the tetrachord which was subjected to a wide variety of divisions, because of the mutability of first note below the top of the tetrachord (paranete or lichanos).
We present here a tabulation and diagram of the notes in a reference tetrachord based on the description of divisions of intervals given by Philolaus.
-- 2,3-monzo --
2 3 ~cents
A [ 0 0 > 0
G [ 3 -2 > -203.9100017
[ -1 1/2 > -249.0224996
F# [ -5 3 > -294.1349974
[ 9/2 -3 > -305.8650026
Gb [ 14 -9 > -317.5950078
[ 10 -13/2 > -362.7075056
F [ 6 -4 > -407.8200035
[ 2 -3/2 > -452.9325013
E [ -2 1 > -498.0449991
Because 53-edo gives an excellent representation of pythagorean tuning (which is the one described by Philolaus for the notes which have integer monzo elements in the above table), doubling its cardinality to obtain 106-edo, we have an excellent simplification of Philolaus's description, as shown on the graphic below. Each interval is labeled with its cents-value (to one decimal place), its name, and its 106-edo degrees.
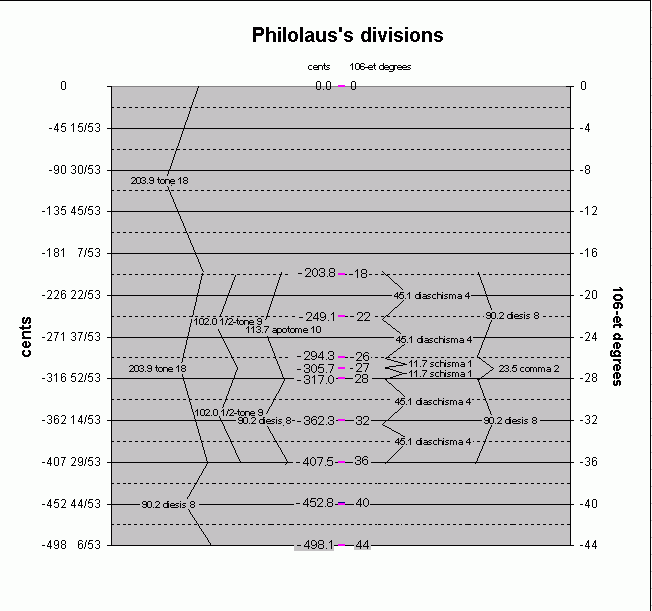
In fact, it is quite probable that this division set out by Philolaus, in which his "comma" is very nearly 1/2 of his "diaschisma", is precisely what led to the idea that the whole-tone is divided into 9 commas, the larger chromatic semitone (apotome) having 5, and the smaller diatonic (limma) having 4 -- which in turn led to the observation that 53-edo is an excellent approximation to pythagorean tuning: if the 8ve is divided diatonically into large and small steps as 5L + 2s, then (5*9) + (2*4) = 45 + 8 = 53.
It is most likely, however, that Philolaus would have demonstrated these divisions on a monochord, in which case he would have used arithmetic integer string-lengths for his measurements. His schisma and diaschisma divisions could be found via the method of katapyknosis by simply doubling the numbers in his ratios, so that the tone would be divided as follows:
~cents
432
> 51.32882843 diaschisma
445
> 49.85071469 diaschisma
458
> 3.77586638 schisma
459
> 3.767649037 schisma
460
> 48.24758687 diaschisma
473
> 46.93935632 diaschisma
486
A similar procedure could be used to divide the diesis at the bottom of the tetrachord, which is needed for the enharmonic genus:
486
> 45.7002020 diaschisma
499
> 44.5247936 diaschisma
512
Indeed, this may be the source for the enigmatic use of 499 as a prime-factor in the enharmonic genus of Boethius himself.
Tabulating all of these ratios gives the following division of the tetrachord:
string ratio ----------------- monzo --------------- ~cents
length 2, 3, 5, 11, 17, 23, 43, 89, 229, 499
A 384 1 : 1 [ 0 > 0.0
G 432 8 : 9 [ 3, -2 > -203.9100017
445 384 : 445 [ 7, 1, -1, 0, 0, 0, 0, -1, 0 > -255.2388302
F# 458 192 : 229 [ 6, 1, 0, 0, 0, 0, 0, 0, -1 > -305.0895449
459 128 : 153 [ 7, -2, 0, 0, -1 > -308.8654112
Gb 460 96 : 115 [ 5, 1, -1, 0, 0, -1 > -312.6330603
473 384 : 473 [ 7, 1, 0, -1, 0, 0, -1 > -360.8806471
F 486 64 : 81 [ 6, -4 > -407.8200035
499 384 : 499 [ 7, 1, 0, 0, 0, 0, 0, 0, 0, -1 > -453.5202055
E 512 3 : 4 [ -2, 1 > -498.0449991
This division does provides intervals which are close in size to the logarithmic divisions specified by Aristoxenos in his description of the movable notes of the various shades of the genera:
- 384:445 = lichanos of relaxed diatonic
- 192:229, 128:153, 96:115 = lichanos of tonic chromatic
- 384:473 = lichanos of hemiolic and relaxed chromatic
- 64:81 = parhypate of both diatonics and tonic chromatic, and lichanos of enharmonic
- 384:499 = parhypate of enharmonic
The only Aristoxenean notes missing from this proposed division of Philolaus are the parhypate of the hemiolic and relaxed chromatic.
REFERENCES
Boethius, Anicius Manlius Torquatus Severinus. c. 505.
manuscript: Cambridge, Trinity College, R.15.22 (944), ff. 48v-65v.
English translation, Fundamentals of music, by Calvin M. Bower.
Yale University Press, New Haven, 1989.
Quotations from Boethius:
|
[Book 3, chapter 5:] Philolaus uero Phytagoricus alio modo tonum diuidere temptauit. statuens scilicet primordium toni. ab eo numero qui primus cubum a primo inpari quod maxime apud Pytagoricos honorabile fuit efficere. Nam cum ternarius numerus primus sit inpar. tres tertio. atque id ter si duxeris XXVII necessario exurgent. qui ad XXIIII numerum tono distat eandem ternarii differentiam seruans. Ternarius enim XXIIII summae octaua pars est quae eidem addita primum a ternario cubum XX ac VII reddit. Ex hoc igitur duas Phylolaus efficit partes. unam quae dimidio fit maior. eamque apotonen uocat. reliquam quae dimidio fit minor. eamque rursus diesim dicit. quam posteri semitonium minus [-f.53v-] appellauere. Harum uero differentiam comma. Ac primum diesim in XIII unitatibus constare arbitratur. eo quod haec inter CCLVI et CCXLIII peruisa sit differentia. quodque idem numerus id est XIII ex nouenario ternario atque unitate consistat. quae unitas puncti obtineat locum. ternarius uero primae inparis lineae nouenarius primi inparis quadrati. Ex his igitur causis cum XIII diesim ponat. quod semitonium nuncupatur: reliquam XXVII numeri partem quae ex XIIII unitatibus continetur. apotomen esse constituit. Sed quoniam inter XIII et XIIII unitas differentiam facit: unitatem loco commatis censet esse ponendam. Totum uero tonum in XXVII unitatibus locat. eo quod inter CCXVI ac CCXLIII qui inter se distant tono XXVII sit differentia. |
How Philolaus divided the tone Philolaus, a Pythagorean, tried to divide the tone in another manner, postulating that the tone had its origin in the number that constitutes the first cube of the first odd number -- for that number was highly revered among the Pythagoreans. Since 3 is the first odd number, if you multiply 3 by 3, then this by 3, 27 necessarily arises, which stands at the distance of a tone from the number 24, and, added to the same, it gives the first cube of 3, 27. From this number, 27, Philolaus made two parts, one that is more than half, which he called the "apotome", and the remainder, which is less than half, which he called the "diesis". (The diesis later came to be called the "minor semitone".) The difference between these he called the "comma". To begin with, Philolaus thought that the diesis consisted of 13 unities, because this had been discerned to be the difference between 256 and 243, and because the same number -- that is, 13 -- consists of 9, 3, and unity, of which unity holds the place of the point, 3 the first odd line, and 9 the first odd square. Because of all this, he identified 13 as the diesis, which he called the "semitone"; the remaining part of the number 27, comprised of 14 unities, he set down to be the apotome. But since unity is the difference between 13 and 14, he said that unity ought to be considered to represent the comma. So he gave the whole tone 27 unities, for 27 is the difference between 216 and 243, which stand at the interval of a tone. |
|
[Book 3, chapter 8:] Phylolaus igitur haec atque his minora spatia. talibus diffinitionibus includit. Diesis inquit est spatium quo est maior sesquitertia proportio duobus tonis. Comma uero est spatium quo maior est sesquioctaua proportio duabus diesibus. id est duobus semitoniis minoribus. Schisma est: dimidium commatis. Diascissma [Diaschissma corr. supra lin.] uero dimidium dieseos: id est semitonii minoris. Ex quibus illud colligitur. quoniam tonus quidem diuiditur principaliter in semitonium minus atque apotomen. Diuiditur etiam in duo semitonia et comma. Quo fit ut diuidatur in quattuor. diaschismata et comma. Integrum uero dimidium toni quod est semitonium constat ex duobus diascismatibus [diaschismatibus corr. supra lin.] quod est unum semitonium minus et scismate [schismate corr. supra lin.]. quod est dimidium commatis. Quoniam enim totus tonus ex duobus semitoniis minoribus et commate coniunctus est: si quis id integre diuidere uelit. faciet unum semitonium minus. commatisque dimidium. Sed unum semitonium minus diuiditur in duo diaschismata. Dimidium uero commatis. unum schisma est. Recte igitur dictum est: integre dimidium tonum in duo diascismata [diaschismata corr. supra lin.]. atque unum scisma [schisma corr. supra lin.] posse partiri. Quo fit ut integrum semitonium a minore semitonio uno schismate differre uideatur. Apotome autem. a minore semitonio: duobus schismatibus differt. Differt enim commate. Sed duo schissmata. unum perficiunt comma. |
Concerning intervals smaller than a semitone Philolaus incorporates these and intervals smaller than these in the following definitions: The diesis, he says, is the interval by which a sesquitertian ratio [4:3] is larger than two tones [(9:8)^2]. The comma is the interval by which the sesquioctave ratio [9:8] is larger than two dieses [(256:243)^2] -- that is, larger than two minor semitones. The schisma is half a comma. The diaschisma is half a diesis -- that is, half a minor semitone. From these definitions it can be concluded that since the tone is first divided into a semitone and an apotome, it is also divided into two semitones and a comma; whence it follows that the tone may be divided into four diaschismata and a comma. So an integral half of a tone (which is a semitone) consists of two diaschismata, which make up one minor semitone, and a schisma, which is half a comma. Since the total tone is joined together from two minor semitones and a comma, if someone wants to divide it equally, he should produce one minor semitone and half a comma. But one minor semitone is divided into two diaschismata, whereas half a comma is one schisma. Therefore it is properly said that half a tone can be properly divided into two diaschismata and one schisma; whence it follows that an integral semitone is seen to differ from a minor semitone by one schisma. An apotome, on the other hand, is different from a minor semitone by two schismata, for it is different by a comma, and two schismata make one comma. |
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
