A gentle introduction to
Fokker periodicity blocks: part 2
[from Monzo: This exposition provides information useful for understanding my concept of finity.]
Last time we saw how choosing a single "unison vector", or interval too small to warrant a distinction in pitch, reduces the infinite resources of 3-limit just intonation (or Pythagorean tuning) to a finite scale. The number of pitches in this scale turned out to be the number of fifths in the chain between the two notes defining the unison vector. Our examples were:
- a pentatonic scale, defined by a unison vector of 5 fifths, a "Pythagorean limma" of 90 cents; and
- a 12-tone scale, defined by a unison vector of 12 fifths, a "Pythagorean comma" of 23 cents.
Now let's consider 5-limit just intonation. It can be considered an infinite succession of 3-limit JI systems, separated by just major thirds (5:4 ratio). Let us put our familiar 3-limit system in the middle, and stack its transpositions by a 5:4 up, upwards, and by a 5:4 down, downwards:
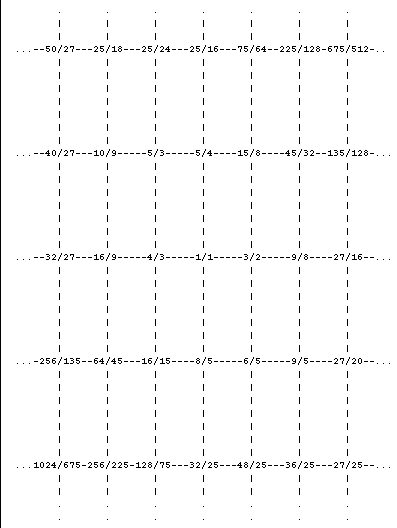
We could have used 5:3 instead of 5:4, but this way is a bit easier to remember: gaining a factor of 3 means moving one place to the right, and gaining a factor of 5 means moving one place upwards.
Now say we again start in the middle (1/1) and start adding notes around it. Unlike the 3-limit case, the direction we move in this lattice may affect which small intervals we end up finding. Say we just look at the notes adjoining 1/1. The interval between 6/5 and 5/4, as well as that between 8/5 and 5/3, is a chromatic semitone or about 71 cents. This interval is always produced on this lattice by moving one step to the left and two steps up. In other words, it corresponds to losing (dividing by) a factor of 3 and gaining (multiplying by) two factors of 5. In vector notation, we may write
(-1 2) = 71 cents. [from Monzo: this is a just "chromatic semitone", ratio 25:24, 2,3,5-monzo [-3 -1, 2 > .]
Unlike the 3-limit case, a single unison vector in the 5-limit lattice does not collapse the infinite pitch variety into a finite set. It may be considered to collapse it into a single vertical line (since every note is equivalent to another note in an adjoining vertical line), or a set of two parallel horizontal lines (since every note is equivalent to a note two horizontal lines away), or a diagonal band, but in any case the number of distinct pitches is still infinite. We need to define one more unison vector to get a finite set of pitches.
If we add a few more notes related by fifths to those adjoining 1/1, we soon find pairs of notes with small intervals between them. The interval between 10/9 and 9/8, as well as that between 16/9 and 9/5, is a syntonic comma or about 22 cents. On the lattice, it corresponds to any move of four steps to the right and one step down:
(4 -1) = 22 cents. [the "syntonic comma", ratio 81:80, 2,3,5-monzo [-4 4, -1 > .]
With these two unison vectors, we may now find a finite set of pitches which is equivalent to the whole infinite lattice. How do we go about this? Fokker's solution was to draw a parallelogram having the two unison vectors as sides. In this case, two opposite sides of the parallelogram would slope one step to the left and two steps up, while the other two sides would slope four steps to the right and one step down. This parallelogram would be wide enough along each of the unison vectors to contain one and only pitch from each equivalence class. Moreover, the parallelogram shape would tile the plane, so that every pitch would fall into one and only one parallelogram. Let us illustrate this for our example:
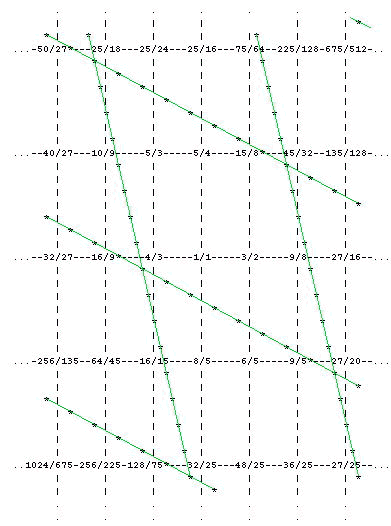
Using our two unison vectors, we have divided the plane into identical parallelograms, each of which has seven lattice points (notes) inside of it. The parallelogram that is completely visible in the diagram above surrounds the ratios that most JI enthusiasts associate with the major scale. Every other parallegram has exactly the same configuration of notes, and each of its notes is equivalent, through trasposition by one or more unison vectors, to one and only one note of the central major scale. Thus we may want to say that the major scale is a periodicity block in the 5-limit lattice.
Unlike the 3-limit case, though, moving the boundaries of the periodicity block does not necessarily lead to the same scale. For example, we could just as easily have drawn our parallelograms like this:
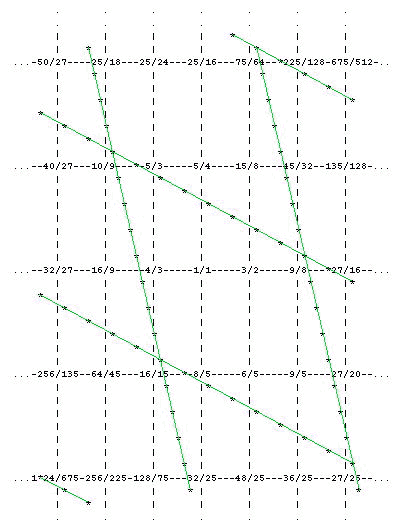
giving the JI minor scale as the periodicity block. This scale is not quite the sixth mode of the major scale; one note needs to be transposed by a syntonic comma to make one scale a mode of the other. Or another possibility is to center the parallelogram on 1/1, giving:
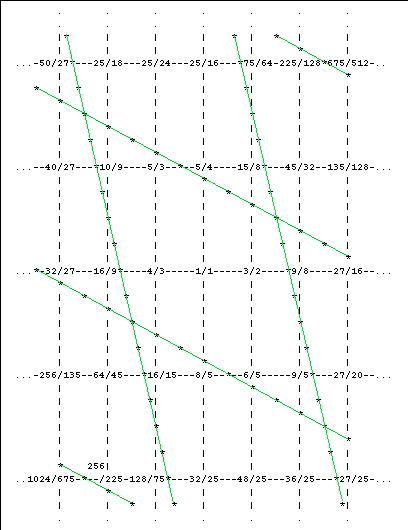
sort of a JI "dorian" scale. In general, then, we can only say that the two unison vectors we have chosen define a periodicity block that is some sort of diatonic scale, but we can't be totally precise as to its JI construction, as any of the notes may be transposed by a unison vector and the important properties of the periodicity block will be maintained.
Mathematically, the unison vectors define 7 equivalence classes in the JI lattice. No matter where we put the paralellograms, each one will have exactly 7 lattice points inside it, equivalent (through unison vectors) to the 7 lattice points inside every other parallelogram. This is true because the area of each parallelogram is exactly 7 (if you consider each step in both directions of the lattice to be of length 1) and it can be proved that a parallelogram of area n whose edges are defined with integer vectors always contains exactly n lattice points no matter where you put it. (If you put an edge right on a lattice point, you can consider it to be 1/2 inside and 1/2 outside the parallelogram, and if you put a corner right on a lattice point, you can consider it to be 1/4 inside, or a fraction determined by the angle of that corner divided by 360 degrees -- either way, you will always end up counting exactly n lattice points inside the parallelogram.)
Is there a way to calculate the area of the parallelogram from the vector representation of the unison vectors? Yes, there is! First, put the unison vectors together into a matrix (the order doesn't matter):
( 4 -1) ( ) (-1 2)
(those are supposed to be big parentheses around the matrix)
Now, calculate the determinant of the matrix:
| 4 -1| | | = 7. |-1 2|
In case you didn't know, the formula for the determinant of a 2-by-2-matrix is:
|a b| | | = a*d - b*c |c d|
If you like geometry, you can convince yourself that this is indeed the formula for the area of a parallelogram whose sides are defined by vectors (a b) and (c d). Don't worry if the determinant comes out negative; you can throw out the minus sign for these purposes.
Let's try another one, since most of us would consider a chromatic semitone a large enough interval to distinguish on our JI instruments. Proceeding to add notes related by a major third to those adjacent to 1/1, we find that 25/16 is close to 8/5, and 5/4 is close to 32/25, the difference in each case being a lesser diesis, or about 41 cents. As a unison vector, this is written:
(0 -3) = 41 cents. [the "diesis", ratio 128:125, 2,3,5-monzo [7 0, -3 > .]
If we take this and the syntonic comma as our two unison vectors, we may draw periodicity blocks like so:
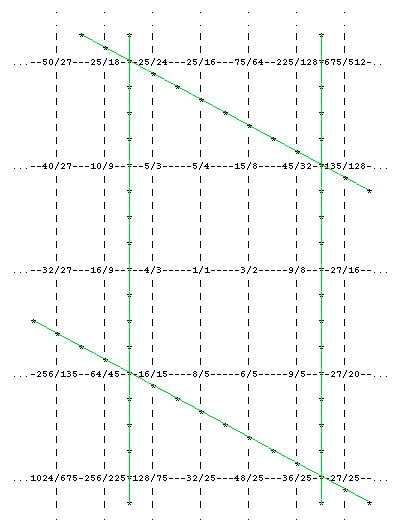
This periodicity block has 12 notes in it, and corresponds to one of the proposals for a 12-tone JI system (was it Ramos?)
[from Monzo: It was De Caus (see Barbour 1951, p 97). The lattice appears in exactly the same form as above in Monzo 1997, JustMusic: A New Harmony. It has been pointed out by Manuel Op de Coul that this periodicity block also defines Ellis's 'Harmonic Duodene' (see Helmholtz 1954, p 461). See also Paul Erlich, Ramos's system as a periodicity-block]
Another famous system defined from the same unison vectors, but only a mode of the other when two notes are transposed by a lesser diesis, is shown here:

[from Monzo: I have been unable to find an advocate of precisely this tuning, which Paul calls a 'famous system'. There is only one pitch placed differently in Fogliano's 'Tuning #1' (see Fogliano 1529, p 36 and Barbour 1951, p 94). The shape is exactly the same as Marpurg's 'monochord number 1' tuning, but tuned down a 2:3 below Marpurg's (see Marpurg 1776, Barbour 1951, p 99, and Monzo 1997).]
Can we verify that these parallelograms always have area 12, and so always define a 12-tone system, from the numbers alone? Yes:
|4 -1| | | = 4*3 - (-1)*0 = 12-0 = 12 |0 -3|
I know this one was much more difficult than the first one, and I'm sure a lot of things could have been explained better. So questions, please, and next time we'll consider some 3-D (7-limit) examples, and we'll have to get a little more abstract since it's hard to show the configuration of soild figures in a 3-D lattice using ASCII text!
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
