Private lessons available in person in San Diego, or online using Discord: composition, music-theory, tuning-theory, piano, and all woodwinds (sax, clarinet, flute, bassoon, recorder). Current rates US$ 80 per hour (negotiable). Send an email to: monzojoe2 (AT) gmail. Also please consider making a donation to Tonalsoft using the PayPal button at the bottom of this page. Thank you.
harmonic entropy
A concept developed by Paul Erlich, measuring the dissonance of an interval based on the uncertainty involved in interpreting that interval in terms of an integer ratio. The underlying mathematics, adapted from Van Eck, appear to confirm Partch's Observation One. Harmonic entropy is intended to be a second component in measuring the sonance of an interval, alongside roughness.
Erlich's actual term is relative harmonic entropy, but the shorter designation has already become standard.
See Paul Erlich, on harmonic entropy, with commentary by Monzo, and also the original version without Monzo's additional commentary, Paul Erlich, on harmonic entropy. Erlich wants it to be noted that this is "a collection of postings, taken out of their original contexts, and strung together without logical progression." See Partch 1974, Genesis of a Music, for additional information on Partch's "Three Observations".
Harmonic entropy is the simplest possible model of consonance. It asks the question, "how confused is my brain when it hears an interval?" It assumes only one parameter in answering this question.
Our brain determines what pitch we'll hear when we listen to a sound. It does so by trying to match the frequencies in the sound's spectrum (timbre) with a harmonic series. The pitch we hear is high or low depending on whether the frequency of the fundamental of the best-fit harmonic series is high or low. The pitch corresponding to the fundamental itself need not be physically present in the sound. Sometimes, the meaning of "best-fit" will not be clear and we'll hear more than one pitch. This happens when several tones are playing together, or when the spectrum of the instrument is highly inharmonic.
Entropy is a mathematical measure of disorder, or confusion. For a dyad, consisting of two tones [definition 3] which are sine waves or have harmonic spectra, one can immediately understand the behavior of the harmonic entropy function. The brain's attempt to fit the stimulus to a harmonic series is quite unambiguous when the ratio between the frequencies is a simple one, such as 2:1 or 3:2. More complex ratios, or irrational ones far enough from any simple one, and the limited resolution with which the brain receives frequency information makes it harder for it to be sure about how to fit the stimulus into a harmonic series. The resolution mentioned is parameterized by the variable s. A computer program is used to calculate the entropy for every possible interval (in, say, 1 cent increments). The set of potential "fitting" ratios is chosen to be large enough (by going high enough in the harmonic series) so that further enlargements of the set cease to affect the basic shape of the harmonic entropy curve.
Here are some examples:
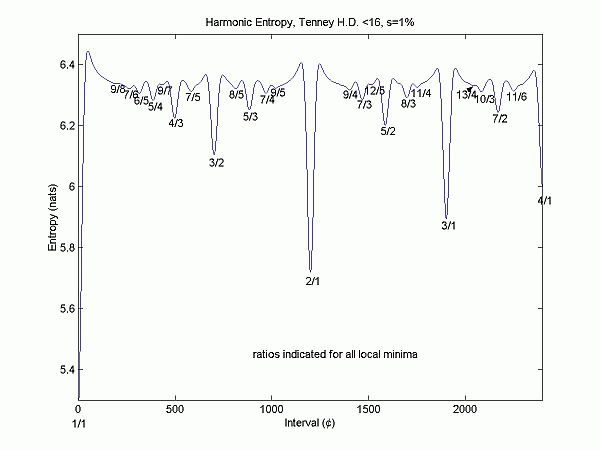
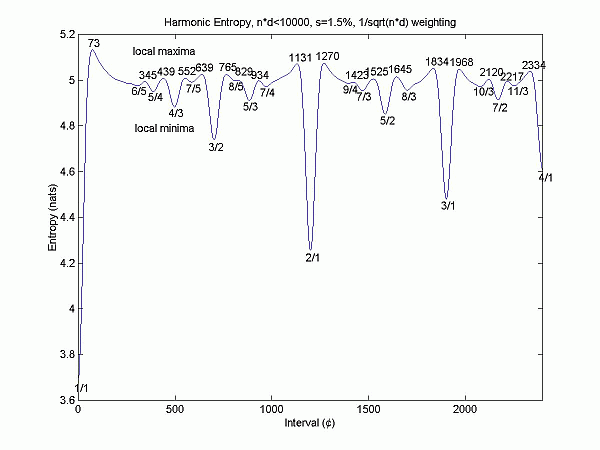
(the "weighting" referred to here is not a weighting of anything in the model but merely refers to a computational shortcut used).
Considering ratios to be different if they are not in lowest terms (appropriate, for example, if we assume 6:3 might be interpreted as the sixth and third harmonics, rather than simply as a 2:1 ratio) leads to this slightly different appearance:
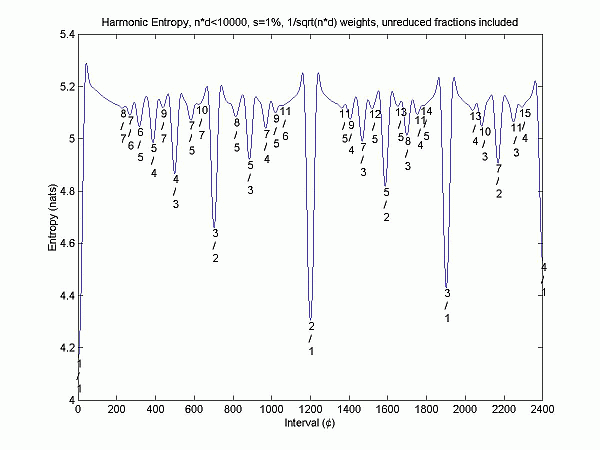
Certain chords of three or more notes blend so well that it sounds like fewer notes are playing than there actually are. We hear a "root" which is kind of the overall pitch of the chord, and the most stable bass note for it. The harmonic entropy of these chords (which is not a function of the harmonic entropies of the intervals in the chord) is low.
Our non-laboratory experiments on the harmonic entropy list seem to conclusively show that the dissonance of a chord can't be even close to a function of the dissonances of the constituent intervals. For example, everyone put the 4:5:6:7 [otonal] chord near the top of their ranking of 36 recorded tetrads from least to most dissonant, while everyone put 1/7:1/6:1/5:1/4 [utonal tetrad] much lower. These two chords have the same intervals. Therefore, it seems to be the case that dissonance measures which are functions of dyadic (intervallic) dissonance account for, at best, a relatively small portion of the dissonance of chords. Such measures include those of Plomp and Levelt, Kameoka and Kuriyagawa, and Sethares.
Harmonic entropy graph with 5 separate curves for different s values:
original EPS format
PDF format
 (PNG format: click graphic to open in full resolution, 5.3 MB)
(PNG format: click graphic to open in full resolution, 5.3 MB)
If you're interested in discussing further, please join the Facebook Microtonal Music and Tuning Theory group.
Please make a donation to help keep Tonalsoft online. A recurring monthly contribution would be apprecitated.
Thank you!
