woolhouse-unit
An interval measurement invented by Wesley S. B. Woolhouse, in his Essay on Musical Intervals [1835], and named "woolhouse-unit" by Joe Monzo in this work.
A woolhouse-unit is the logarithmic division of the octave into 730 equal parts. It is calculated as the 730th root of 2, or 2(1/730), with a ratio of approximately 1:1.000949968. It is an irrational number.
The formula for calculating the Woolhouse-unit-value of any ratio r is: woolhouse-units = log10(r) * [730 / log10(2)] or woolhouse-units = log2(r) * 730
Woolhouse created this unit specifically as a small logarithmic measurement to compare interval sizes, because the values for the basic 5-limit intervals which concerned him -- the octave, the two sizes of just intonation "whole-tones", and the diatonic semitone (which he non-standardly called limma) -- are all very close to integer values, making it easy to do computations disregarding fractional or decimal remainders, without accumulating too much error.
[Woolhouse 1835, p 18]
It will be useful to divide the octave into such a number of equal divisions that each interval of the scale may comprise an integral number of them ... such as will render the major and minor-tones and limma whole numbers, since all other intervals result from the various combinations of these elemental ones.
interval ratio ~Woolhouse-units octave 2/1 730 major-tone 9/8 124.0452511 minor-tone 10/9 110.9622582 limma 16/15 67.96986521
A table of integral woolhouse-unit values for various intervals follows:
Woolhouse-units 3,5-monzo ratio interval
1 [ 8, 1 > 32805/32768 skhisma
12 [-4,-2 > 2048/2025 diaschisma
13 [ 4,-1 > 81/80 syntonic comma
14 [12, 0 > 531441/524288 pythagorean comma
25 [ 0,-3 > 128/125 enharmonic diesis
43 [-1, 2 > 25/24 small chromatic semitone
56 [ 3, 1 > 135/128 large chromatic semitone
68 [-1,-1 > 16/15 diatonic semitone
111 [-2, 1 > 10/9 small whole-tone
124 [-1,-1 > 16/15 large whole-tone
167 [ 1, 2 > 75/64 augmented-2nd
179 [-3, 0 > 32/27 pythagorean trihemitone
192 [ 1,-1 > 6/5 just minor-3rd
235 [ 0, 1 > 5/4 just major-3rd
248 [ 4, 0 > 81/64 pythagorean ditone
303 [-1, 0 > 4/3 perfect-4th
427 [ 1, 0 > 3/2 perfect-5th
470 [ 0, 2 > 25/16 augmented-5th
495 [ 0,-1 > 8/5 minor-6th
538 [-1, 1 > 5/3 major-6th
563 [-1,-2 > 128/75 diminished-7th
594 [ 2, 2 > 225/128 augmented-6th
606 [-2, 0 > 16/9 pythagorean minor-7th
619 [ 2,-1 > 9/5 just minor-7th
More precise values (to one decimal place) are shown on this 5-limit lattice-diagram:
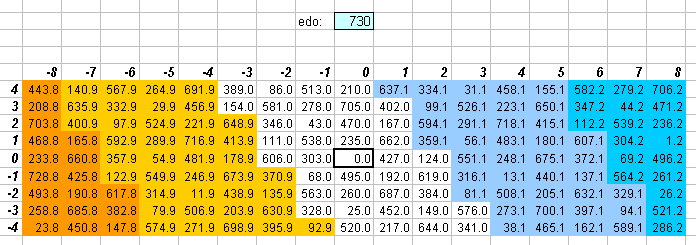
(Shades of blue and orange designate error plus and minus, respectively, of the actual Woolhouse-unit values from the integral values. See the "Gallery of EDO error lattices" for a full explanation.)
woolhouse-units calculator
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
