quarter-tone / 24-edo / 24-ed2
1. general meaning: half a semitone
"Quarter-tone" is used in a general sense by many people to refer to microtonal intervals approximately half as large as the semitone, or thus measuring approximately 50 cents.
The earliest confirmed written reference to an interval in this size range is by Philolaus, who called it a "diaschisma". There is less of a tendency to use "quarter-tone" in this general sense today.
2. one degree of 24-edo
Used as an exact measurement, the quarter-tone is calculated as the 24th root of 2, or 2(1/24), an irrational proportion with the approximate ratio of 1:1.029302236643, and an interval size of exactly 50 cents.
The quarter-tone is the size of one degree, and thus the basic "step" size, in the 24-eq (or 24-ET or 24-edo) scale, also called the "quarter-tone scale" or system.
Several composers began writing music in 24-ET early in the 20th century, including Charles Ives, Richard Stein, Jörg Mager Willi Möllendorf, Ivan Vyschnegradsky, and Alois Hába. Hába had several instruments specially built to be playable in this system, and Schoenberg, Webern, and Berg also experimented with quarter-tones.
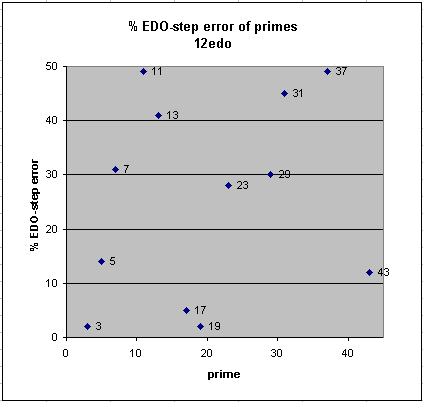
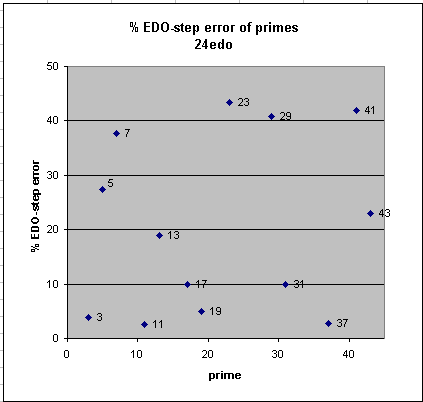
Below are graphs of the error of 12-edo and 24-edo for approximations to the prime-factors up to 43, given as a percentage of one degree of each tuning. It can easily be seen that the big improvements of 24-edo over 12-edo are the approximations to prime-factors 11, 13, 31, and 37.
|
|
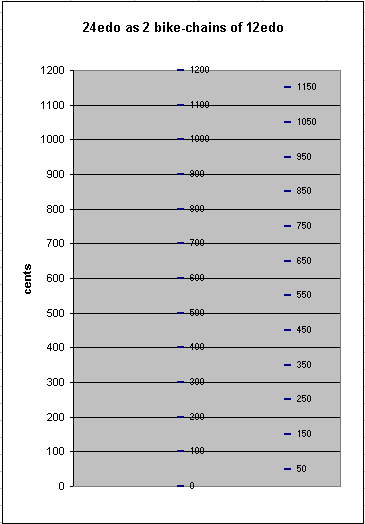
In the 5-limit, 24-edo does not provide more accurate approximations to the basic intervals (3/2, 5/4, 6/5, and their octave-complements) than 12-edo, thus, it is best viewed as 2 bike-chains of 12-edo, a quarter-tone apart. In fact, this is exactly the approach taken by Möllendorf, who called this tuning "bichromatic".
24-edo approximates the following 13-limit ratios within the usually-accepted human tuning error of about 5 cents:
-- 24-edo -- ---------------- just intonation -----------------
--------- monzo ------- ~cents error
deg cents 2 3, 5 7 11, 13 ratio ~cents of 24-edo from JI
23 1150 [ -4 4, 1 0 0, -1 > 405 : 208 1153.60605556 -3.60605556
23 1150 [ -1 -2, 1 1 0, 0 > 35 : 18 1151.22961860 -1.22961860
23 1150 [ 6 -1, 0 0 -1, 0 > 64 : 33 1146.72705677 +3.27294323
21 1050 [ -1 -1, 0 0 1, 0 > 11 : 6 1049.36294150 +0.63705850
21 1050 [ 6 0, -1 -1 0, 0 > 64 : 35 1044.86037967 +5.13962033
19 950 [ -2 5, -1 -1 0, 0 > 243 : 140 954.63538399 -4.63538399
19 950 [ 1 -1, -1 0 0, 1 > 26 : 15 952.25894704 -2.25894704
19 950 [ -1 2, 1 0 0, -1 > 45 : 26 949.69605383 +0.30394617
19 950 [ 2 -4, 1 1 0, 0 > 140 : 81 947.31961687 +2.68038313
17 850 [ 1 2, 0 0 -1, 0 > 18 : 11 852.59205937 -2.59205937
17 850 [ 2 -3, 0 0 1, 0 > 44 : 27 845.45293977 +4.54706023
15 750 [ -6 2, 0 0 1, 0 > 99 : 64 755.22794410 -5.22794410
15 750 [ 1 3, -1 -1 0, 0 > 54 : 35 750.72538226 -0.72538226
15 750 [ 4 -3, -1 0 0, 1 > 208 : 135 748.34894531 +1.65105469
15 750 [ 2 0, 1 0 0, -1 > 20 : 13 745.78605210 +4.21394790
13 650 [ -3 -1, 1 1 0, 0 > 35 : 24 653.18461947 -3.18461947
13 650 [ 4 0, 0 0 -1, 0 > 16 : 11 648.68205764 +1.31794236
11 550 [ -3 0, 0 0 1, 0 > 11 : 8 551.31794236 -1.31794236
11 550 [ 4 1, -1 -1 0, 0 > 48 : 35 546.81538053 +3.18461947
9 450 [ -1 0, -1 0 0, 1 > 13 : 10 454.21394790 -4.21394790
9 450 [ -3 3, 1 0 0, -1 > 135 : 104 451.65105469 -1.65105469
9 450 [ 0 -3, 1 1 0, 0 > 35 : 27 449.27461774 +0.72538226
9 450 [ 7 -2, 0 0 -1, 0 > 128 : 99 444.77205590 +5.22794410
7 350 [ -1 3, 0 0 -1, 0 > 27 : 22 354.54706023 -4.54706023
7 350 [ 0 -2, 0 0 1, 0 > 11 : 9 347.40794063 +2.59205937
5 250 [ -1 4, -1 -1 0, 0 > 81 : 70 252.68038313 -2.68038313
5 250 [ 2 -2, -1 0 0, 1 > 52 : 45 250.30394617 -0.30394617
5 250 [ 0 1, 1 0 0, -1 > 15 : 13 247.74105296 +2.25894704
5 250 [ 3 -5, 1 1 0, 0 > 280 : 243 245.36461601 +4.63538399
3 150 [ -5 0, 1 1 0, 0 > 35 : 32 155.13962033 -5.13962033
3 150 [ 2 1, 0 0 -1, 0 > 12 : 11 150.63705850 -0.63705850
1 50 [ -5 1, 0 0 1, 0 > 33 : 32 53.27294323 -3.27294323
1 50 [ 2 2, -1 -1 0, 0 > 36 : 35 48.77038140 +1.22961860
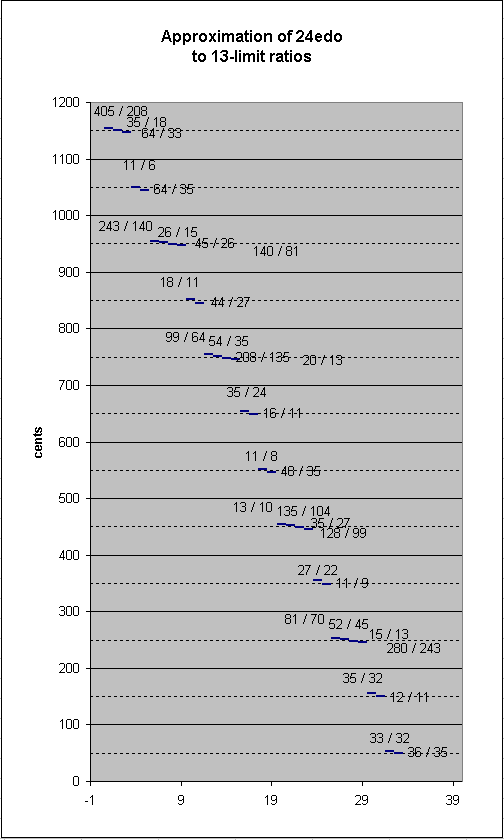
Below is a lattice-diagram showing the ratios in the above table.
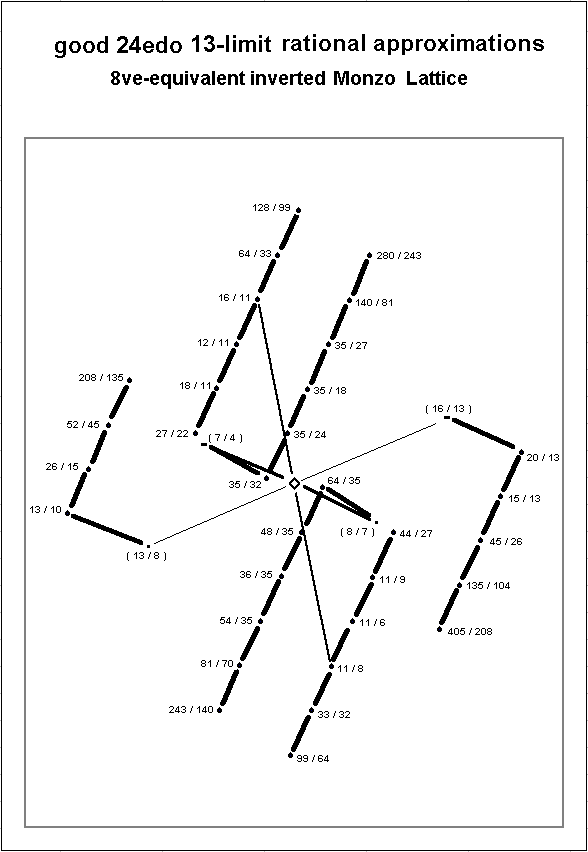
It can be seen in general that 24-edo gives a good representation of pythagorean chains of ratios whose individual terms (numerator and denominator) contain 11 or (5 and 7), or whose terms compare prime-factors (5 and 13).
Below is a table of a pythagorean approximation to quarter-tone tuning, a system of tuning-by-concords which is entirely symmetrical on the negative and positive sides from 1/1, in terms of generator 3/2 5ths and 4/3 4ths. The table is arranged in descending order of pitch.
1/4-tone . (3/2)^x . ~cents error . (24).... (2/1) ...... 0 .. 23 ..... -24 ...... +3.08 .. 22 ....... 5 ...... +9.78 .. 21 ...... 22 ...... -6.99 .. 20 ...... -2 ...... -3.91 .. 19 ..... -26 ...... -0.83 .. 18 ....... 3 ...... +5.87 .. 17 ..... -21 ...... +8.94 .. 16 ...... -4 ...... -7.82 .. 15 ...... 25 ...... -1.12 .. 14 ....... 1 ...... +1.96 .. 13 ..... -23 ...... +5.03 .. 12 ....... 6 ..... +11.73 .. 11 ...... 23 ...... -5.03 .. 10 ...... -1 ...... -1.96 ... 9 ..... -25 ...... +1.12 ... 8 ....... 4 ...... +7.82 ... 7 ...... 21 ...... -8.94 ... 6 ...... -3 ...... -5.87 ... 5 ...... 26 ...... +0.83 ... 4 ....... 2 ...... +3.91 ... 3 ..... -22 ...... +6.99 ... 2 ...... -5 ...... -9.78 ... 1 ...... 24 ...... -3.08 ... 0 ....... 0 ....... 0 Arranged in order by generator number, the tuning goes like this: -26, -25, -24, -23, -22, -21, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 21, 22, 23, 24, 25, 26
Joe Monzo invented a notation based on the quarter-tone scale, which he calls the quarter-tone staff.
An interval of about 50 cents (¢), one half of a tempered semitone. [By "tempered", Chalmers here means specifically 12-edo.]
Typical quarter tones in Just Intonation have ratios such as 36/35 or 33/34.
"In 1905-6 the Kitab al-musiqa al-sharqi ('The book of eastern music') by Kamil al-Khula'i (1879-1938) established the equidistance of quartertones in the octave. This scale of 24 quarter-tones was the subject of fierce discussion at the Congress of Cairo in 1932, where the participants divided into two opposing camps; the Egyptians supported the division of the octave into 24 equal quarters, while the Turks (represented by Yekta Bey) and the Syro-Lebanese (Sabra and Tawfiq al-Sabbagh) rejected the system of equal division.
In 1959 and 1964 the Egyptians organized two symposia to settle the differences of opinion arising from the controversy at the 1932 Congress over the equidistance of quarter-tones. The aim of these symposia was to establish the principle of equal temperament on the basis of the quarter-tone and give official sanction to its teaching."
quarter-tones calculator
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by selecting the highest level of financial support that you can afford. Thank you.
