Vicentino's "2nd tuning of 1555" is composed of two chains of 1/4-comma meantone, the first one a 19-tone chain from Gb to B#, which can be closely approximated by a 19-tone subset of 31edo, and the second a 17-tone chain from Gb to A#, 1/4-comma higher than the first chain.
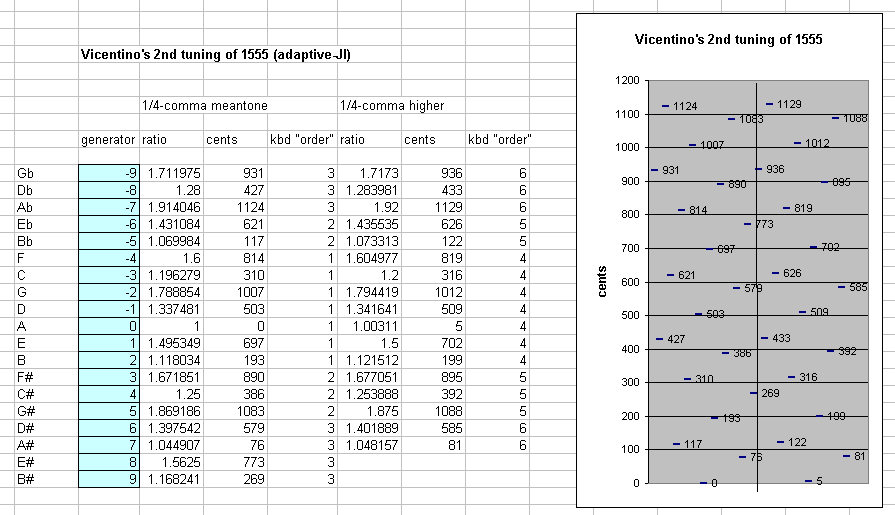
here's a rectangular lattice-diagram of Vicentino's "2nd tuning of 1555"; the 3-axis is horizontal, the 5-axis is vertical and the pitches indicate exponents which increase by increments of 1/4. notes a "5th" apart (3:2 ratio) which have integer exponents of 5 are connected by dashed lines. Approximate cents-values are given after the note-names.
B# 269
E# 773-----
A# 76
D# 579 A# 81
G# 1083 D# 585
C# 386-----G# 1088
F# 890 C# 392
B 193 F# 895
E 697 B 199
A 0-----E 702
D 503 A 5
G 1007 D 509
C 310 G 1012
F 814-----C 316
Bb 117 F 819
Eb 621 Bb 122
Ab 1124 Eb 626
Db 427-----Ab 1129
Gb 931 Db 433
Gb 936
the 19-tone "first chain" is the column on the left-hand side of this lattice.
the generator "5th" in 1/4-comma meantone can be factored as 5^(1/4), thus 4 steps of the generator (i.e., 4 "5ths") is exactly 5^1, which represents the 5:4 ratio; thus, 4 "5ths" = a "major-3rd", the basic equation of meantone, which is only approximately true in other variants belonging to the meantone family of temperaments, but is exact here in 1/4-comma MT. thus, on the lattice, a chain of 1/4-comma meantone goes straight up and down the 5-axis.
Vicentino's second chain, 1/4-comma higher than the first chain, thus ends up being in effect a 3:2 higher than the first chain, as the lattice shows in the right-hand column. Thus, it is an adaptive-JI which provides a great number of vertical sonorities which are in exact 5-limit just-intonation, but without the problems of commatic drift, since it is based on meantone.
here's an attempt at redrawing the same lattice in triangular format:
B# 269
E# 773 ----------
A# 76 '.
D# 579 '. A# 81
G# 1083 '. D# 585
C# 386 ------------- G# 1088
F# 890 '. C# 392
B 193 '. F# 895
E 697 '. B 199
A 0 ---------------- E 702
D 503 '. A 5
G 1007 '. D 509
C 310 '. G 1012
F 814 -------------- C 316
Bb 117 '. F 819
Eb 621 '. Bb 122
Ab 1124 '. Eb 626
Db 427 ------------- Ab 1129
Gb 931 Db 433
Gb 936
the lattices show that the following triads are exactly in tune to low-integer proportions:
Major = 4:5:6
Gb, Db, Ab, Eb, Bb, F, C, G, D, A, E, B, F#, C#, G#
minor = 1/(6:5:4)
eb, bb, f, c, g, d, a, e, b, f#, c#, g#, d#
here is the whole scale. i'd have to do some reading to find out Vicentino's notation, so i'll just use a plus sign to designate the 1/4-comma-higher note of each like-named pair.
note ~cents {3,5}-vector 12edo note w/ cawapus
Ab+ 1129 [1 -8/4] G#/Ab +1201
Ab 1124 [0 -7/4] G#/Ab +981
G#+ 1088 [1 4/4] G#/Ab -481
G# 1083 [0 5/4] G#/Ab -701
G+ 1012 [1 -3/4] G +501
G 1007 [0 -2/4] G +280
Gb+ 936 [1 -10/4] F#/Gb +1482
Gb 931 [0 -9/4] F#/Gb +1261
F#+ 895 [1 2/4] F#/Gb -200
F# 890 [0 3/4] F#/Gb -420
F+ 819 [1 -5/4] F +781
F 814 [0 -4/4] F +561
E# 773 [0 8/4] F -1121
E+ 702 [1 0/4] E +80
E 697 [0 1/4] E -140
Eb+ 626 [1 -7/4] D#/Eb +1061
Eb 621 [0 -6/4] D#/Eb +841
D#+ 585 [1 5/4] D#/Eb -621
D# 579 [0 6/4] D#/Eb -841
D+ 509 [1 -2/4] D +360
D 503 [0 -1/4] D +140
Db+ 433 [1 -9/4] C#/Db +1341
Db 427 [0 -8/4] C#/Db +1121
C#+ 392 [1 3/4] C#/Db -340
C# 386 [0 4/4] C#/Db -561
C+ 316 [1 -4/4] C +641
C 310 [0 -3/4] C +420
B# 269 [0 9/4] C -1261
B+ 199 [1 1/4] B -60
B 193 [0 2/4] B -280
Bb+ 122 [1 -6/4] A#/Bb +921
Bb 117 [0 -5/4] A#/Bb +701
A#+ 81 [1 6/4] A#/Bb -761
A# 76 [0 7/4] A#/Bb -981
A+ 5 [1 -1/4] A +220
A 0 [0 0/4] A 0
below is an interval matrix of Vicentino's adaptive-JI:
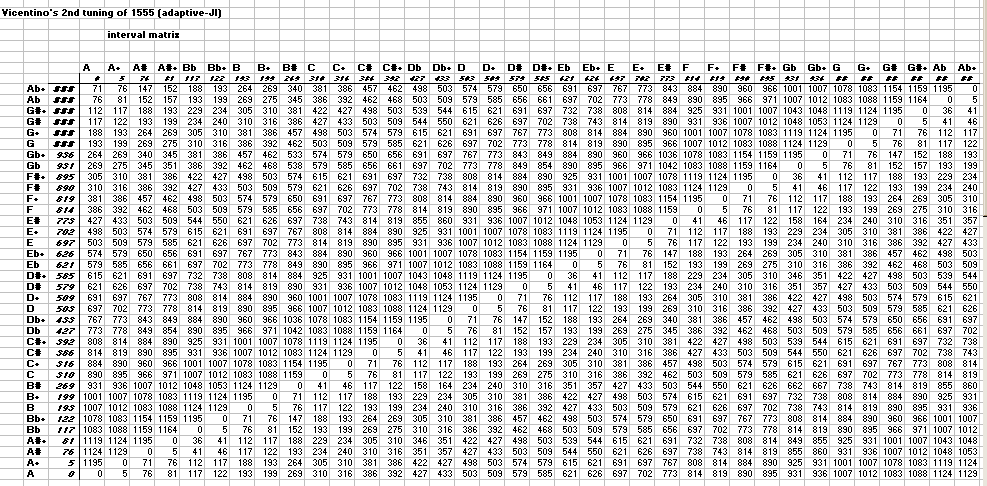
just out of curiosity i analyzed what intervals might approximate the 7:4 ratio (~969 cents). here's the list:
~971 cents:
Gb : E+
F : D#+
Eb : C#+
Db : B+
C : A#+
Bb : G#+
Ab : F#+
~966 cents:
G : E#
Gb+ : E+
Gb : E
F+ : D#+
F : D#
Eb+ : C#+
Eb : C#
D : B#
Db+ : B+
Db : B
C+ : A#+
C : A#
Bb : G#
Bb+ : G#+
Ab+ : F#+
Ab : F#
The graphic below shows the 36-out-of-217edo approximation of Vicentino's tuning. With a maximum error of ~2 cents, which is nearly half the difference between Vicentino's two chains, 217edo was chosen less because of its accuracy than because of the fact that, as 7 bike-chains of 31edo, each higher than the last by 1 degree of 217edo (which is close to 1/4 of a comma), its structure resembles that of Vicentino's tuning so well; therefore, a 36-tone subset of 217edo (19 tones from the first 31edo bike-chain, plus 17 tones from the next bike-chain above it) can work on the same principles as those of Vicentino's actual tuning.
217edo provides, among other things, an excellent set of pitches to achieve fixed-pitch adaptive-JI. A subset of 217edo which consists of 2 bike-chains of 31edo, approximately 1/4-comma apart, provides a good approximation to Vicentino's tuning. (See below, on Margo Schulter's and Paul Erlich's 62-tone proposals.)
Below is an example by Dave Keenan of a I-VI-II-V-I
"comma-pump"
chord progression, written in the "sagittal" notation
developed by he and George Secor in 2002, and tuned
by me in 217edo (click on the graphic to hear the MIDI-file).
Below are two musical illustrations of the first 5 measures of
Orlando di Lasso's motet Ave regina coelorum, tuned
in Vicentino's adaptive-JI tuning. This example was chosen
because it is used as an illustration by Easley Blackwood
of the unsuitability of strict-JI for "common-practice" repertoire
(see Blackwood 1985, p 133-135). The first illustration uses
Pythagorean tuning
as the basis for the letter-names and
accidentals, and
shows the deviation of Vicentino's tuning from Pythagorean.
The second illustration uses
1/4-comma meantone
as the notational basis and shows the deviation of Vicentino's
tuning from that. [click on the illustration
to hear a MIDI-file of it]
Vicentino, Nicola. 1555.
L'antica musica ridotta alla moderna prattica
["ancient music restored to modern practice"]
Antonio Barre, Rome. republished 1557.
English translation:
Blackwood, Easley. 1985.
The Structure of Recognizable Diatonic Tunings
Princeton University Press, Princeton, NJ.
ISBN 0-691-09129-3
Paul Erlich commented, in Yahoo tuning list message 40414 (Thu Oct 31, 2002 4:37 am):
hi monz,
nice work! really, it's the meantone chain itself that should be latticed -- the 19-tone chain is a 5-limit periodicity block with 81:80 tempered out, of course . . . the slight difference between the chains allows one to obtain pure JI sonorities, but doesn't affect the basic structure or function of the scale.
i like what you're saying about 217-equal, but see below.
perhaps a more impressive coincidence is that 1/4-comma meantone, if carried out beyond 31 notes, actually repeats itself about 6 cents away -- close to 1/4-comma! along these lines, margo schulter has proposed a 62-tone 1/4-comma meantone chain as a marvelous tuning system, since it practically encompasses vicentino's tuning while allowing one to circulate around the cycle of 31 meantone fifths (or thirds or whatever). this is an example of an NMOS (currently being discussed on tuning-math), since 62 = 2 * the 31-tone MOS of meantone . . . other NMOSs are helmholtz 24 and groven 36, multiples of the 12-tone MOS of schismic temperament . . .
. . . if you take a look, i'm sure you'll find that 205-equal provides a much better approximation of vicentino's tuning than 217- equal does. 205-equal also gives a better approximation, than 217- equal, of schulter 62, but 174-equal positively excels in the latter regard.
Margo Schulter commented, in Yahoo tuning list message 40451 (Thu Oct 31, 2002 4:57 pm):
Hello, there, everyone, and I'd like quickly to clarify a slight distinction between my 62-note proposal of 2001, and Paul Erlich's ingenious proposal for a single 62-note chain of 1/4-comma meantone.
My proposal has two 31-note chains of 1/4-comma meantone at 1/4-comma apart (~5.38 cents), and thus represents a kind of superset including in essence both of Vicentino's archicembalo tunings.
Vicentino's first tuning is a circulating 31-note meantone "loop" (to use Joe Pehrson's term) plus a few extra "comma keys" which in one interpretation add a few just fifths to the most common diatonic notes of the tuning.
The second tuning, discussed in this thread and in the new Monz web page, consists of a basic 19-note tuning (Gb-B#) on the main manual, with the second manual (ideally 19 notes, but 17 notes in Vicentino's practical instrument) providing "just fifths" to all or most of these notes. This arrangement is generally synonymous with two meantone chains at 1/4-comma apart.
In my 62-note tuning, each 31-note set is a complete cycle or loop (as in Vicentino's first tuning), with the two sets 1/4-comma apart (as in his second tuning). The advantage of this arrangement is that one can play enharmonic compositions involving fifthtone steps (about 1/5-tone, and actually slightly unequal at 128:125 or ~41.06 cents for the larger fifthtone and ~34.99 cents for the smaller fifthtone) in adaptive JI.
In the 62-note system which you describe, Paul, we have the slightly different although musically almost equivalent arrangement of a single 62-note meantone chain, with the second 31-note set thus at a distance of about 6.07 cents from the first set -- very close to the ~5.38 cents required for pure vertical 5-limit JI (4:5:6 or 10:12:15).
What you give is an excellent [example] of where one can both "have one's cake and eat it too" with a circulating loop. Each 31-note set could serve as a complete meantone cycle; but the 62-note chain makes available virtually pure JI sonorities which would not be available in a single 31-note tuning.
Similarly, while 53 notes makes a fine circulating Pythagorean loop, carrying the chain to 106 notes makes available virtual JI intervals such as the near-7:6 minor third formed from 68 fourths up -- thanks to Monz for pointing this out!
With Paul's 62-note meantone chain, the near-equivalence between the 6.07-cent difference of 31 meantone fifths vs. 18 pure octaves and the adaptive-JI adjustment of 1/4-comma (~5.38 cents) makes such a result possible. With the Pythagorean example, it is the close resemblance between the comma of Mercator (53 pure fifths vs. 31 pure octaves), about 3.62 cents, and the 3-7 schisma at about 3.80 cents, differing only by a nanisma.
Anyway, while my original 62-note proposal followed the apparent historical method of Vicentino's "just fifths," Paul's described alterative of a single 62-note meantone chain nicely shows the potential of "almost-closed" circulating loops.
Updated: