A tonal lattice with 12 nodes invented by A. J. Ellis as a model for the 12-tone chromatic scale in Just Intonation.
It consists of a chain of four perfect-5ths (F:C:G:D) and three major-3rds above and below each of these pitch tones.
Analogs may be constructed by replacing the 3/2 and 5/4's with other intervals.
[from John Chalmers, Divisions of the Tetrachord]
..............................
Ellis's Duodene was the original inspiration for my own independent invention of what I used to call "matrices", as published in my initial paper JustMusic prime-Factor Musical Notation, and which I now refer to, in keeping with the work done by others before me, as lattices.
The Duodene is a periodicity-block whose unison-vectors are the syntonic comma and the enharmonic diesis (definition 4). Here is a Monzo lattice of Ellis's Duodene:
Unison-vectors:
81:80 = [4 -1] syntonic comma
128:125 = [0 -3] Ellis's "great diesis", Rameau's "minor diesis", typically called "enharmonic diesis"
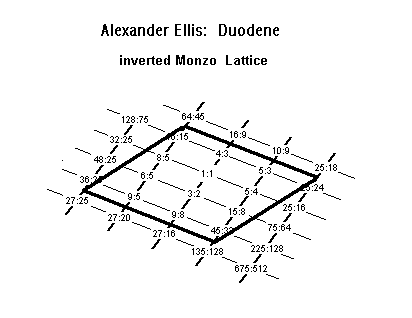
[from Joe Monzo, JustMusic: A New Harmony]
..............................
See also:
Ellis's Duodene as a Periodicity-Block;
Paul Erlich's derivation of the duodene in Gentle Introduction to Fokker Periodicity Blocks, part 2.
My webpage, Ellis's Duodene and a "best-fit" meantone.
