The interval which encompasses 5 degrees of a diatonic scale. It is usually close in size to the frequency ratio 3:2, which is approximately 702 cents.
In the usual 12-edo tuning, the perfect 5th encompasses 7 semitones, and is thus exactly 700 cents. This is the precise dividing point between tunings of the historically important meantone and pythagorean families, and 12-edo can function as a tuning of both families. The primary difference between those two families, in terms of the use of the diatonic-scale in "common-practice", is that in the historically precedent pythagorean tuning, the diatonic-semitone (the minor-2nd, called limma in ancient terminology) is the smaller of the two different-sized semitones, and the chromatic-semitone (the augmented-prime or augmented-unison, called apotome in ancient terminology) is the larger of the two, whereas in the later meantone tunings exactly the reverse is true: the meantone diatonic-semitone is larger and the meantone chromatic-semitone is smaller. In 12edo, both types of semitones are exactly the same size, 100 cents: therefore, no 5th smaller than 12-edo's 5th of 700 cents can function as a pythagorean 5th, and no 5th larger than 700 cents can function as a meantone. (See the 12-edo article for a detailed explanation of why 12-edo belongs to both families).
Below is a graph of the size of the best approximation to the 3:2 "5th" in cents, for all the EDOs from 10 to 72:
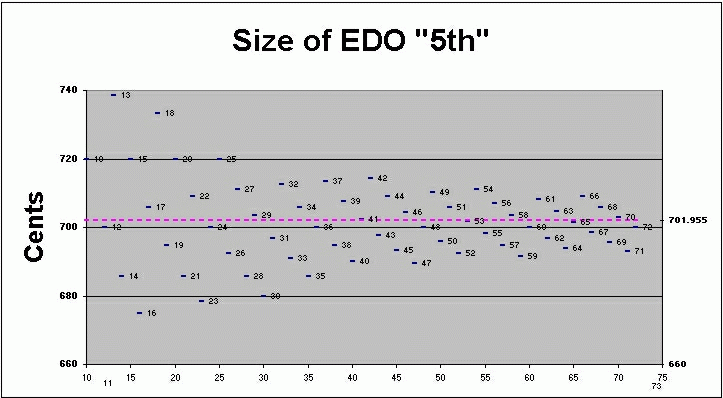
Below is a table showing the sizes of "perfect-5th" for various tunings of the historically important pythagorean and meantone families, in descending order of size in cents:
tuning ~cents of generator (243:160 ratio 723.4612904621024 5-limit JI "super-5th": 3:2 * 81:80 [syntonic-comma]) pythagorean: 3\5-edo 720.0 also: 6\10, 9\15, 12\20, 15\25, 18\30, 21\35, etc. (approximate upper limit of what is recognizably a "perfect-5th") 22\37-edo 713.5135135135135 16\27-edo 711.1_ also: 32\54, 48\81, ... 320\540 90\152-edo 710.5263157894736 13\22-edo 709.0909090909091 319\540-edo 708.8888888888889 85\144-edo 708.3_ 53\90-edo 706.6_ also: ... 159\270, ... 318\540 183\311-edo 706.1093247588425 10\17-edo 705.8823529411766 also: 20\34, 30\51 317\540-edo 704.4444444444445 27\46-edo 704.3478260869565 17\29-edo 703.448275862069 also: 34\58, 51\87 89\152-edo 702.6315789473684 24\41-edo 702.439024390244 also: 120\205 127\217-edo 702.3041474654378 182\311-edo 702.250803858521 79\135-edo 702.2_ also: 158\270, 316\540 55\94-edo 702.1276595744681 3:2 ratio 701.9550008653874 pythagorean "perfect-5th" 31\53-edo 701.8867924528302 38\65-edo 701.5384615384614 ---------------------- 12-edo 700.0 also: 14\24, 21\36, 28\48, 35\60, 42\70, 49\84, 56\96, ... 84\144, ... 315\540 ---------------------- meantones: 1/11-comma 699.9998836293224 60\103-edo 699.029126 53\91-edo 698.901099 46\79-edo 698.734177 181\311-edo 698.3922829581994 39\67-edo 698.507463 1/6-comma 698.3706193 32\55-edo 698.181818 57\98-edo 697.959184 157\270-edo 697.7_ also: 314\540 25\43-edo 697.674419 1/5-comma 697.6537429 3/14-comma 697.3465102 43\74-edo 697.297297 2/9-comma 697.1758254 61\105-edo 697.142857 18\31-edo 696.7741935483871 also: 36\62, ... 126\217-edo 1/4-comma 696.5784285 65\112-edo 696.428571 47\81-edo 696.296296 7/26-comma 696.164846 29\50-edo 696.0 5/18-comma 695.9810315 2/7-comma 695.8103467 40\69-edo 695.652174 313\540-edo 695.5_ 51\88-edo 695.454545 62\107-edo 695.327103 1/3-comma 694.7862377 11\19-edo 694.7368421052631 also: 22\38, 33\57, ... 88\152-edo 180\311-edo 694.5337620578779 15\26-edo 692.3076923076923 19\33-edo 690.909090909091 23\40-edo 690.0 4\7-edo 685.7142857142857 also: 8\14, 12\21, 16\28, 20\35 ... etc. (approximate lower limit of what is recognizably a meantone perfect-5th) (40:27 ratio 680.4487112686725 5-limit JI "wolf-5th": 3:2 / 81:80 [syntonic-comma])
