"Interval" refers to a set containing two musical pitches, the pitch distance between those pitches, or to a microtonal music journal.
Exactly synonymous with dyad, which see.
The size of the pitch space between two different pitches, or the section of the linearly-perceived pitch-continuum bounded by those two pitches.
Any number of mathematical expressions may be used to describe the size of an interval, but three are far more common than any others:
In standard music-theory, the ordinal numbers actually count the number of letters inclusive between the lower and higher note, with "A" following after "G" in ascending order; thus, for example, one "5th" occurs between lower note "F" and higher note "C": F G A B C.
When using the ordinal number method, a further qualification is often given, describing the ordinal number as "major", "minor", "perfect", "augmented", or "diminished", depending on whether or not one or two of the notes in the interval are "natural", "flat", "sharp", "double-flat", or "double-sharp".
The ordinal-number classification has two basic categories of intervals:
In addition to these "basic" categories, an interval may also be "augmented", which means that it is slightly larger than "perfect" or "major", or "diminished", which means that it is slightly smaller than "perfect" or "minor". For example:
Tables are given below showing the number of EDO degrees for each of the standard intervals (within one octave) in some of the important meantone tunings, beginning with the familiar 12-et.
In the usual 12-tone equal temperament ("12-ET"), the diatonic-semitone and chromatic-semitone are exactly the same size and are thus equivalent, both being sometimes referred to as "half-steps", and resulting in an equivalency between some of the intervals. For example, the "augmented-5th" described above is still a type of "5th" because it subtends the letters F G A B C, regardless of the fact that the "C" at the top of the interval is actually a "C#". In 12-ET, where "C#" is exactly the same as "Db", there is an interval of exactly the same size (8 "half-steps") but with a different name: the "minor-6th" between F:Db, which subtends the 6 letters F G A B C D, with the "D" at the top actually a "Db". Below is a table for 12-ET, showing how intervals (within one octave) are categorized, and the number of logarithmic "half-steps" in each interval (within one octave):
body of table indicates number of 12edo semitones ("1/2-steps")
+---------++-----------+---------------------------------+-----------+
|interval || |(imperfect): perfect :(imperfect)| |
| name || diminished| minor : : major | augmented |
+=========++===========+===========:=========:===========+===========+
| || | : : | |
| prime || -1 | -- : 0 : -- | 1 |
+---------++-----------+---------------------------------+-----------+
| 2nd || 0 | 1 : -- : 2 | 3 |
+---------++-----------+---------------------------------+-----------+
| 3rd || 2 | 3 : -- : 4 | 5 |
+---------++-----------+---------------------------------+-----------+
| 4th || 4 | -- : 5 : -- | 6 |
+---------++-----------+---------------------------------+-----------+
| 5th || 6 | -- : 7 : -- | 8 |
+---------++-----------+---------------------------------+-----------+
| 6th || 7 | 8 : -- : 9 | 10 |
+---------++-----------+---------------------------------+-----------+
| 7th || 9 | 10 : -- : 11 | 12 |
+---------++-----------+---------------------------------+-----------+
| 8ve || 11 | -- : 12 : -- | 13 |
+---------++-----------+---------------------------------+-----------+
In contrast to this, in 19-tone equal temperament ("19-ET"), the "flats" and "sharps" do not display the same equivalence as in 12-ET, and therefore each tone ("whole-step") is divided not into two "half-steps" or semitones, but into 3 "third-tones", in which the "augmented-prime" ("chromatic-semitone") subtends 1 "1/3-tone" and the "minor-2nd" ("diatonic-semitone") subtends 2 "1/3-tones". Using the same example as that for 12-ET, we can see that in 19-ET the "augmented-5th" thus subtends 12 "1/3-tones" but the "minor-6th" subtends 13 "1/3-tones". 19-ET does have a set of intervallic equivalences, but they are different from those in 12-ET: we can see, for example, that in 19-ET, the augmented-5th F:C# subtends the same number of 1/3-tones as the diminished-6th F:Dbb. Below is a table for 19-ET, showing how intervals are categorized, and the number of logarithmic "1/3-tones" in each interval:
body of table indicates number of 19edo 1/3-tones
+---------++-----------+---------------------------------+-----------+
|interval || |(imperfect): perfect :(imperfect)| |
| name || diminished| minor : : major | augmented |
+=========++===========+===========:=========:===========+===========+
| || | : : | |
| prime || -1 | -- : 0 : -- | 1 |
+---------++-----------+---------------------------------+-----------+
| 2nd || 1 | 2 : -- : 3 | 4 |
+---------++-----------+---------------------------------+-----------+
| 3rd || 4 | 5 : -- : 6 | 7 |
+---------++-----------+---------------------------------+-----------+
| 4th || 7 | -- : 8 : -- | 9 |
+---------++-----------+---------------------------------+-----------+
| 5th || 10 | -- : 11 : -- | 12 |
+---------++-----------+---------------------------------+-----------+
| 6th || 12 | 13 : -- : 14 | 15 |
+---------++-----------+---------------------------------+-----------+
| 7th || 15 | 16 : -- : 17 | 18 |
+---------++-----------+---------------------------------+-----------+
| 8ve || 18 | -- : 19 : -- | 20 |
+---------++-----------+---------------------------------+-----------+
In 31-tone equal temperament ("31-ET"), each tone ("whole-step") is divided in 5 "fifth-tones" or "dieses", in which the "augmented-prime" ("chromatic-semitone") subtends 2 "1/5-tones" and the "minor-2nd" ("diatonic-semitone") subtends 3 "1/5-tones". Note that with the standard set of 31 notes (i.e., the 7 nominals and the set of nominals with associated flats, sharps, double-flats, and double-sharps, which arranged in a chain-of-5ths runs from Gbb to Ax), 31-ET does not have any equivalent pairs of intervals: thus, each interval is not only considered distinct in theory, but actually is distinct in its own unique tuning. Below is a table for 31-ET, showing how intervals are categorized, and the number of "1/5-tones" in each interval:
body of table indicates number of 31edo 1/5-tones
+---------++-----------+---------------------------------+-----------+
|interval || |(imperfect): perfect :(imperfect)| |
| name || diminished| minor : : major | augmented |
+=========++===========+===========:=========:===========+===========+
| || | : : | |
| prime || -2 | -- : 0 : -- | 2 |
+---------++-----------+---------------------------------+-----------+
| 2nd || 1 | 3 : -- : 5 | 7 |
+---------++-----------+---------------------------------+-----------+
| 3rd || 6 | 8 : -- : 10 | 12 |
+---------++-----------+---------------------------------+-----------+
| 4th || 11 | -- : 13 : -- | 15 |
+---------++-----------+---------------------------------+-----------+
| 5th || 16 | -- : 18 : -- | 20 |
+---------++-----------+---------------------------------+-----------+
| 6th || 19 | 21 : -- : 23 | 25 |
+---------++-----------+---------------------------------+-----------+
| 7th || 24 | 26 : -- : 28 | 30 |
+---------++-----------+---------------------------------+-----------+
| 8ve || 29 | -- : 31 : -- | 33 |
+---------++-----------+---------------------------------+-----------+
In 55-tone equal temperament ("55-ET"), each tone ("whole-step") is divided in 9 "ninth-tones" or "commas", in which the "augmented-prime" ("chromatic-semitone") subtends 4 "1/9-tones" and the "minor-2nd" ("diatonic-semitone") subtends 5 "1/9-tones". As with 31-ET, note that with the standard set of 31 notes (i.e., the 7 nominals and the set of nominals with associated flats, sharps, double-flats, and double-sharps, which arranged in a chain-of-5ths runs from Gbb to Ax), 55-ET does not have any equivalent pairs of intervals: thus, each interval is not only considered distinct in theory, but actually is distinct in its own unique tuning. This conception of interval size is arguably the one which is most applicable to the repertoire of "common-practice" music. Below is a table for 55-ET, showing how intervals are categorized, and the number of "1/9-tones" in each interval:
body of table indicates number of 55edo 1/9-tones
+---------++-----------+---------------------------------+-----------+
|interval || |(imperfect): perfect :(imperfect)| |
| name || diminished| minor : : major | augmented |
+=========++===========+===========:=========:===========+===========+
| || | : : | |
| prime || -4 | -- : 0 : -- | 4 |
+---------++-----------+---------------------------------+-----------+
| 2nd || 1 | 5 : -- : 9 | 13 |
+---------++-----------+---------------------------------+-----------+
| 3rd || 10 | 14 : -- : 18 | 22 |
+---------++-----------+---------------------------------+-----------+
| 4th || 19 | -- : 23 : -- | 27 |
+---------++-----------+---------------------------------+-----------+
| 5th || 28 | -- : 32 : -- | 36 |
+---------++-----------+---------------------------------+-----------+
| 6th || 33 | 37 : -- : 41 | 45 |
+---------++-----------+---------------------------------+-----------+
| 7th || 42 | 46 : -- : 50 | 54 |
+---------++-----------+---------------------------------+-----------+
| 8ve || 51 | -- : 55 : -- | 59 |
+---------++-----------+---------------------------------+-----------+
For tables of interval sizes in other 12-tone tunings, see
For intervals of 7-tone diatonic scales, see
For a huge list of 11-
For detailed data on specific diatonic intervals, see:
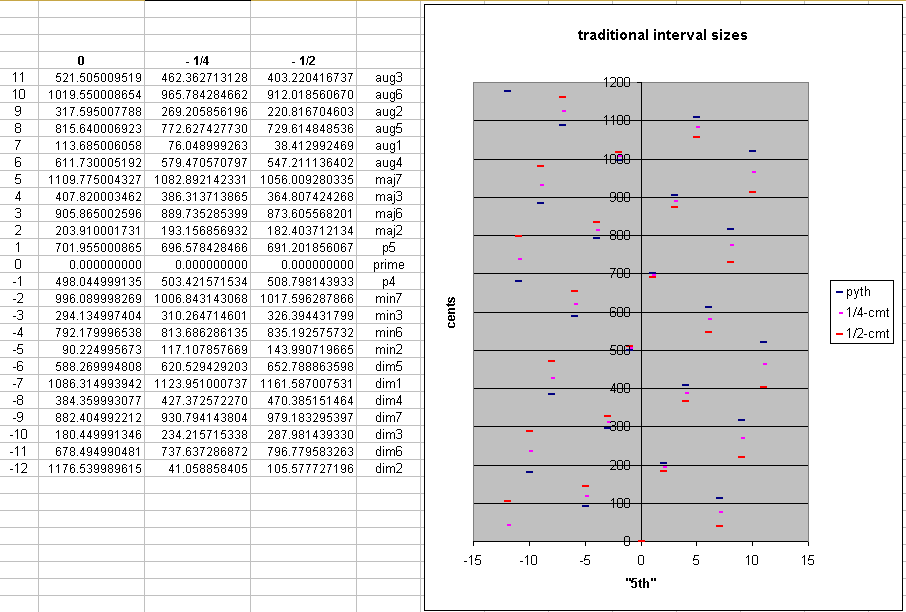
Below is a table and graph of the range of sizes for all of the standard diatonic intervals found in a 12-tone tuning, for tunings ranging from 1/2-comma meantone to pythagorean. 1/4-comma meantone is also shown for comparison.
The name of a journal concerned with microtonal music and theory, founded by Jonathan Glasier in San Diego in 1978 and published regularly until 1987. For more information, see John Pusey's Table of Contents.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.