chromatic semitone / augmented-prime / #1
A diatonic interval which is the difference between the tone (i.e., whole-tone) and the diatonic semitone. In several different theories of the medieval, Renaissance, Baroque, and Classical periods, a distinction was made between chromatic and diatonic semitones, as there were two different sizes of semitone in many tuning systems. (Two good examples are pythagorean and meantone.)
The chromatic semitone is the interval between two notes of a scale which both have the same nominal (letter-names in the case of the traditional theory explained here), but which have different accidentals (including the natural), for example, A - A#. The implication is that only one of the two is a bonafide diatonic scale degree. This interval is called the "augmented prime" and may be found abbreviated as aug1, #1, or +1 .
The chromatic semitone arose out of ancient Greek tetrachord theory, by the fact that the Perfect Immutable System includes both the Lesser Perfect System (with its tetrachord
- E nete diezeugmenon
|
tetrachord | D paranete diezeugmenon D nete synemmenon -
diezeugmenon | | tetrachord
| C trite diezeugmenon C paranete synemmenon | synemmenon
- B paramese |
tone of < Bb trite synemmenon |
disjunction A mese A mese -
The interval-sizes may be shown schematically thus ("t" = tone, "s" = diatonic semitone, "(t-s)" = chromatic semitone):
t
______________
| |
s (t-s) s
A Bb B C
|______________|
t
In the pythagorean [3-limit] system, the chromatic semitone is also called the apotome.
Note that in positive systems (typical example: pythagorean tuning), the chromatic semitone is larger than the diatonic, while in negative systems (typical example: any meantone tuning) it is exactly the opposite and the diatonic is the larger.
Typical meantone chromatic semitones range in size from about 63 to 100 cents. Below is a table and pitch-height graph of the size of the chromatic semitone for several historical meantones:
meantone adjustment of 81/64 "flavor" --- [pythagorean 'major 3rd'] --- ----- 2,3,5-monzo ----- ~ cents 1/11-comma ((3/2)7) / (22) / ((81/80)(7*1/11)) = [-93/11 49/11, 7/11 > = 99.99918541 1/6-comma ((3/2)7) / (22) / ((81/80)(7*1/6)) = [-19/3 7/3 , 7/6 > = 88.59433486 1/5-comma ((3/2)7) / (22) / ((81/80)(7*1/5)) = [-27/5 7/5 , 7/5 > = 83.57620062 3/14-comma ((3/2)7) / (22) / ((81/80)(7*3/14)) = [ -5/1 1/1 , 3/2 > = 81.42557166 2/9-comma ((3/2)7) / (22) / ((81/80)(7*2/9)) = [-43/9 7/9 , 14/9 > = 80.2307778 1/4-comma ((3/2)7) / (22) / ((81/80)(7*1/4)) = [ -4/1 0 , 7/4 > = 76.04899926 7/26-comma ((3/2)7) / (22) / ((81/80)(7*7/26)) = [-45/13 -7/13, 49/26 > = 73.15392182 5/18-comma ((3/2)7) / (22) / ((81/80)(7*5/18)) = [-29/9 -7/9 , 35/18 > = 71.86722073 2/7-comma ((3/2)7) / (22) / ((81/80)(7*2/7)) = [ -3 -1 , 2 > = 70.67242686 [the ratio 25:24] 1/3-comma ((3/2)7) / (22) / ((81/80)(7*1/3)) = [ -5/3 -7/3 , 7/3 > = 63.50366367
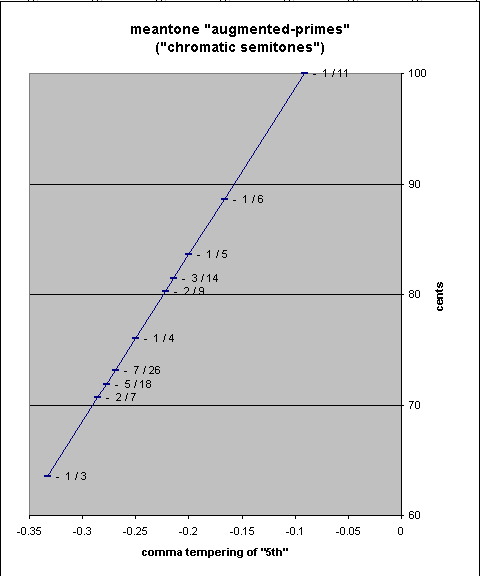
Note that the JI ratio [ -3 -1, 2 > = 25:24 is rendered exactly in 2/7-comma meantone, and that another JI ratio which falls within this range, and which also vanishes in meantone (because it is a syntonic-comma larger than 25:24), is [ -3 -1, 2 > + [ -4 4, -1 > = [-7 3, 1 > = 135:128 = ~ 92.17871646 cents.
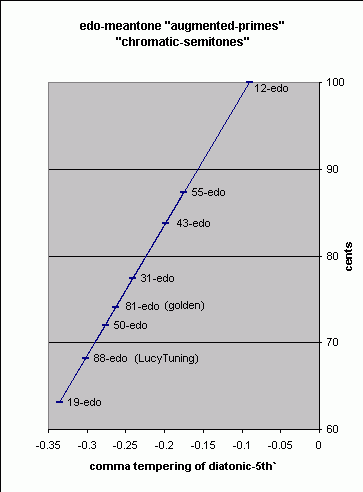
Below is a table and pitch-height graph of the size of the chromatic semitone for several edo-meantones:
edo ratio of meantone generator ~cents 12-edo 2( 7/12) 100 55-edo 2(32/55) 87.27272727 43-edo 2(25/43) 83.72093023 31-edo 2(18/31) 77.41935484 81-edo 2(47/81) 74.07407407 (~ golden meantone) 50-edo 2(29/50) 72 88-edo 2(51/88) 68.18181818 (~ LucyTuning) 19-edo 2(11/19) 63.15789474
Marchetto of Padua specified three types of semitone and called the third, naturally enough, the enharmonic; however, his names were matched with the intervals differently than in traditional theory.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
