
The 'square' of all possible intervals in a closed (finite) tuning system.
The matrix or square is generated by listing each note in the scale both horizontally and vertically, assuming one note to be at the top of the interval and the other to be at the bottom, then filling in the size of the interval where both lines intersect.
When each interval is measured as an absolute value, half of the intervals will have positive sizes and half will have negative, with all intervals falling within the octave bounded by the 'tritone' below the 1/1 and the 'tritone' above it.
Usually, for the values which would be negative, the higher note in the interval is raised an 'octave', so that all intervals fall within the 'octave' bounded by 1/1 and 2/1, as in this example.
Illustrated below are some interval matrices for various EDO tunings, along with their closest fixed equivalent subset of 72-edo. (Note that allowing flexible use of 72-edo for notational purposes would give some pitches as different degrees than those given here, giving a better approximation but at the same time introducing inconsistencies.) All intervals are given in Semitones in the top two comparison charts, and in 72-edo degrees (moria) and fractions thereof in the chart below them.
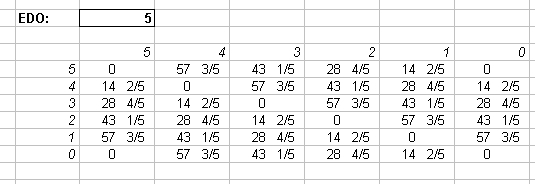
Interval Matrices of 5-edo and its closest 72-edo equivalent:
in Semitones
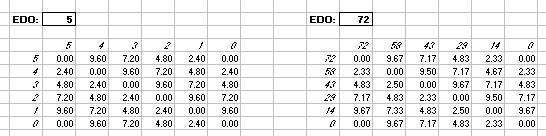
in 72-edo degrees (moria):
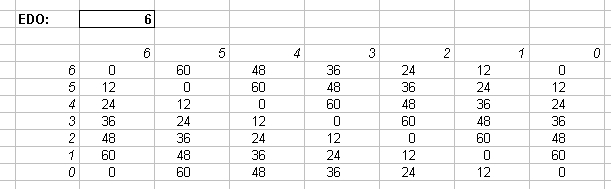
The Interval Matrix of 6-edo (the whole-tone scale) is reproduced by its exact equivalent in 72-edo of degrees 0, 12, 24, 36, 48, and 60:
In 72-edo-degrees (moria):
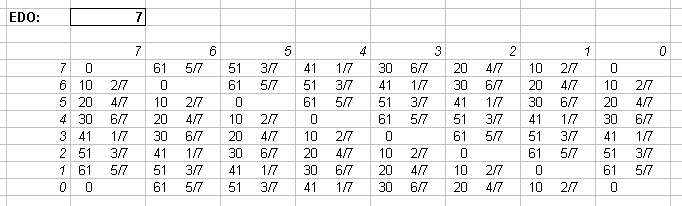
Interval Matrices of 7-edo and its closest 72-edo equivalent:
in Semitones

in 72-edo degrees (moria):
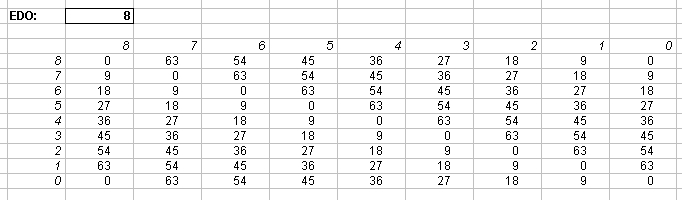
Interval Matrices of 8-edo and its exact 72-edo equivalent:
in Semitones
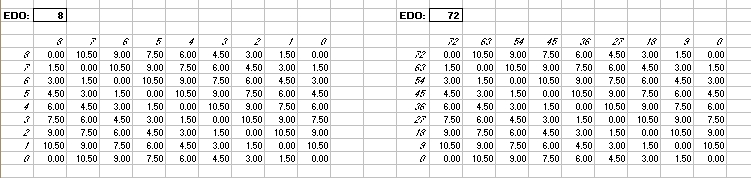
in 72-edo degrees (moria):
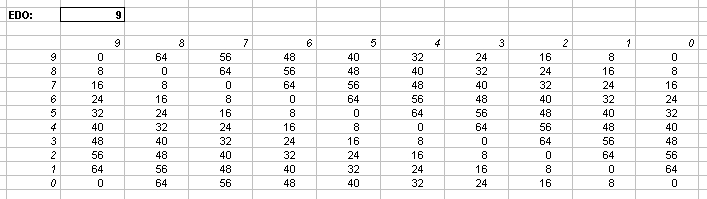
Interval Matrices of 9-edo and its exact 72-edo equivalent:
in Semitones
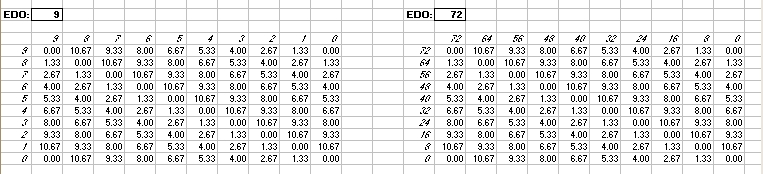
in 72-edo degrees (moria):
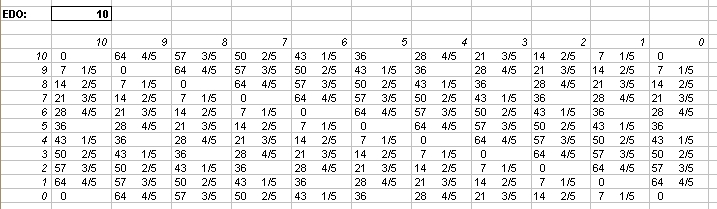
Interval Matrices of 10-edo and its closest 72-edo equivalent:
in Semitones
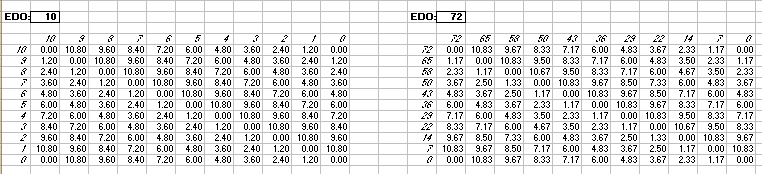
in 72-edo degrees (moria):
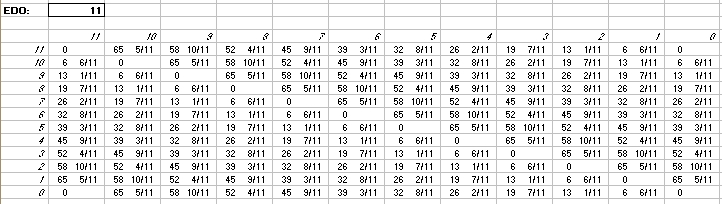
Interval Matrices of 11-edo and its closest 72-edo equivalent:
in Semitones
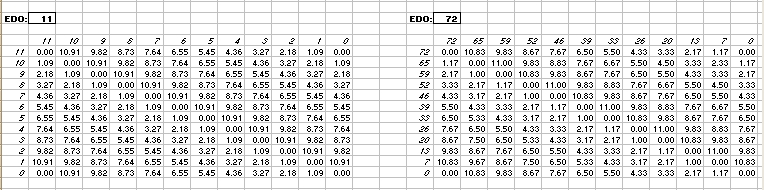
in 72-edo degrees (moria):
The interval matrix of 12-edo is reproduced by its exact equivalent in 72-edo of degrees 0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, and 66. Thus the interval set can be expressed by these moria.
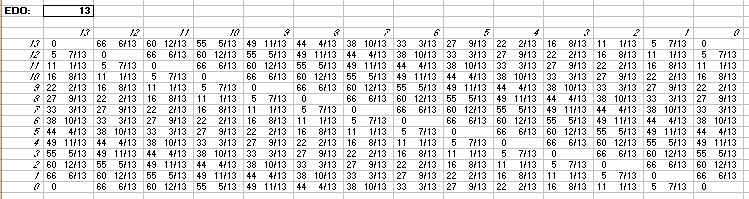
And last is an interval matrix of 13-edo given only in 72-edo degrees (moria):
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.