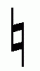
One of the five standard accidentals used in Western musical notation. The meaning of the natural symbol is to cancel the effect of a previous use, on the note named by the same letter nominal, of one of the other four accidentals (sharp, flat, double-sharp, double-flat); this previous use may be that of an individual accidental or that of a key-signature.
For example, if the key-signature specifies that all F's are to be made F#, or if F does not have an acciental in the key-signature and an accidental F# appears earlier in the measure, the natural sign on a subsequent F indicates that that occurrence is to be the "white-key" F (referring to the standard Halberstadt keyboard).
The naturals refer to the notes which are designated by the unadorned letter-name nominals A, B, C, D, E, F, G. They are represented on the piano keyboard by all of the white keys. These seven notes together, in this order, comprise the heptatonic diatonic A natural minor scale. This scale is shown in its pythagorean tuning thus, on a lattice diagram in 3-prime-space:
F C G D A E B ---+-----+-----+-----+-----+-----+-----+- -4 -3 -2 -1 0 1 2 = exponent of prime-factor 3 128:81 32:27 16:9 4:3 1:1 3:2 9:8 = ratio
This particular lattice is a periodicity-block formed by the unison-vector known as the "apotome", the pythagorean chromatic semitone, which would be shown as 7 steps on the lattice (if the lattice were big enough):
interval name prime-factor 2,3-monzo ratio ~cents
apotome 37 [* 7, > 2187/2048 113.6850061
This scale was viewed by music theorists as least as far back as ancient Greece as the most basic musical scale -- this is the reason for the word "natural" to describe this set of notes.
The specific pitch values (cents, ratios, frequencies ... whatever) of the notes have changed over the course of history. Some of the primary changes to be noted are:
D ------ A ----- E ----- B
[-1,0> [0,0> [1,0> [2,0>
4:3 1:1 3:2 9:8
\ / \ / \ /
\ / \ / \ /
\ / \ / \ /
F ------- C ----- G
[0,-1> [1,-1> [2,-1>
8:5 6:5 9:5
The reference pitch eventually shifted to C, changing the geometry of the lattice slightly:
A ----- E ----- B
[-1,1> [0,1> [1,1>
5:3 5:4 15:8
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
F ------ C ----- G ----- D
[-1,0> [0,0> [1,0> [2,0>
4:3 1:1 3:2 9:8
This form of the diatonic scale was adopted by Ben Johnston as the set of naturals in his notation.
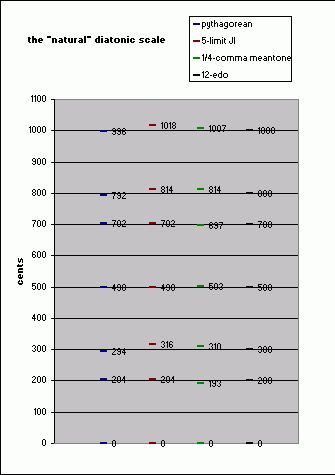
Below is a pitch-height graphic showing these four types of natural diatonic scales:
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.