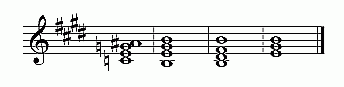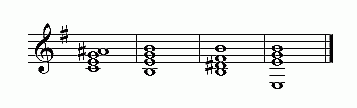A diatonic interval which is one chromatic semitone larger than the "major-6th" of the diatonic scale. The augmented-6th is composed of 4 tones (i.e., whole-tones), one diatonic semitone, and one chromatic semitone. For example, in the key of C:
_________________major-6th_______________
| |
C D E F G A B = C-major diatonic scale
t t s t t t
M2 M2 m2 M2 M2 M2
chromatic semitone
/ \
C A A# B
(t-s) s
+1 m2
|________________augmented-6th_______________|
augmented-6th = 4t + s + (t-s) = 5(t-s) + 5s
= 4(M2) + m2 + (+1) = 5(+1) + 5(m2)
The augmented-6th is thus composed of 5 chromatic semitones and 5 diatonic semitones (or equivalently, 5 augmented-primes and 5 minor-2nds). In 12-edo the augmented-6th is composed of 10 equal semitones, and thus is enharmonically equivalent (i.e., the same size) as the minor-7th, however, in every other tuning (except those which are multiples of 12-edo) these are two different intervals.
The "augmented-6th" arose primarily out of "common-practice" harmony as part of a cadence, where the two notes which form the "augmented-6th" each resolve in contrary motion (opposite directions) onto the "5th" of the scale, as the chord also changes either directly to the dominant (V), or first to the tonic in 2nd inversion (I 6-4) and then to the dominant (V).
The resulting "augmented-6th chord" could come in three varieties:
In terms of meantone generators, a meantone "German-6th" chord would be mapped to the chain of "5ths" like this, if C is the reference note:
----- ----- ----- ------ | C | | G | D A | E | B F# C# G# D# | A# | | 0 | | 1 | 2 3 | 4 | 5 6 7 8 9 | 10 | ----- ----- ----- ------
This particular German-6th chord, C:E:G:A#, would be used in the keys of E-major or E-minor, as follows:
E-major:
A# => B ---- B ----- B
G => G# => F# => G#
E --- E => D# => E
C => B ---- B => E
6
bVI+6 I 4 V I
|
E-minor:
A# => B ---- B ----- B
G --- G => F# => G
E --- E => D# => E
C => B ---- B => E
6
bVI+6 I 4 V I
|
It will be noticed that, in the standard familiar 12-tone equal-temperament ("12-et") tuning, because it contains pairs of notes which exhibit enharmonic-equivalence, the German-6th chord is identical in pitch to an equivalent "dominant-7th" chord. For example, because A# and Bb are the same pitch in 12-et, the C:E:G:A# chord illustrated above is equivalent to C:E:G:Bb .
The generator "5th" size of 12-et (700 cents) makes it one of the limiting ends of the meantone family of temperaments. All other meantones will have an A# which is lower in pitch than that meantone's Bb, and so on for all other pairs of notes which are enharmonically-equivalent in 12-et.
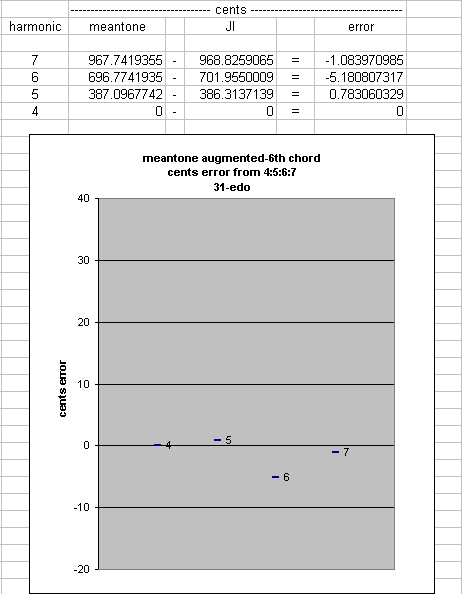
The A#/Bb pitch-class of 12-et (= exactly 1000 cents) is ~ 31.17409353 cents higher than the harmonic minor-7th of ratio 7:4 (= ~ 968.8259065 cents). Therefore, the augmented-6th of other meantones will be a narrower interval than that in 12-et, and it will approach the 7:4 ratio as the generator "5th" of the meantone gets smaller and smaller, until, at a point where the amount of tempering (narrowing) of the generator is ~ 0.235857059 of a syntonic-comma (~ 5.072410218 cents, very nearly 25/106-comma), the augmented-6th is exactly a 7:4 ratio. (Common meantones near the "optimal" value are 1/4-comma and 31-et, as can be seen in the mouse-over applet below.) After that point, as the meantone generator "5th" continues to decrease in size, its augmented-6th becomes smaller than 7:4 .
Because:
Below is a comparison of various meantone "German-6th" chords showing their proportions in relation to 4:5:6:7
1/6-comma 4.0 : 5.020747126 : 5.987590331 : 7.060425645 43-edo 4.0 : 5.012677419 : 5.985182958 : 7.032089773 55-edo 4.0 : 5.018557437 : 5.986937385 : 7.05273004 31-edo 4.0 : 5.002262078 : 5.982071529 : 6.995618488 1/4-comma 4.0 : 5.0 : 5.981395125 : 6.98771243 2/7-comma 4.0 : 4.99113464 : 5.978741999 : 6.956779315 1/3-comma 4.0 : 4.979338607 : 5.975206329 : 6.915748066 19-edo 4.0 : 4.978770358 : 5.975035847 : 6.913775146
For something which is probably more meaningful, here are graphs of the cents-errors of various meantones to the 4:5:6:7 tetrad:
|
MouseOver the names of the various meantone chains (circles for EDOs) without clicking, to see a graph of the cents-errors from the JI 4:5:6:7 tetrad.
12-edo
|
|
Message 55625
From: "monz"
Date: Mon Aug 16, 2004 1:39 pm
Subject: Re: The "out of tune" harmonics in the Harmonic Series
Haresh:
--- In tuning@yahoogroups.com, "akjmicro"
Can you please show me the aesthetics (or, logic) behind the 7th partial (b-sesquiflat) having been most unceremoniously shoved off into oblivion in connection with JI ? In fact, the 7th, 11th, 13th and the 14th harmonics occur naturally as a part of the Harmonic series, but are considered out of tune in the ordinary twelve-tone scales. Do we take this to mean that the notes falling in line with the JI concept are more important than these naturally occurring notes?
a big part of the reason why ratios of 7 were not canonically admitted into Western harmony in modern times, is that not long after 5 was finally accepted (c.1480), the lute and then a few centuries later the keyboard became the preeminent instruments, and the physical structure of both, encouraged musicians to want to limit their scales to only 12 notes. (of course, there were experiments with larger tuning systems, but 12 was the norm.)
at first, these 12 notes were generally tuned in meantone, then around 1700 well-temperaments became popular, which brought the scale overall closer to 12edo, then finally from 1800-1900 12edo itself solidified into the standard tuning ... and 12edo is not so great at emulating ratios of 7, with error from JI for those ratios typically around 30 cents or ~1/7-tone.
it is true that many meantones (especially 1/4-comma) give an excellent representation of the 7th partial but spelled as an "augmented-6th" (i.e., A# sounds like "B sesquiflat"). the similarity of this chord to a 4:5:7 triad ("Italian 6th") or 4:5:6:7 tetrad ("German 6th") probably caused composers to enjoy employing it. [see the applet above]
but until some serious is research is done, examining together the the occurence of possible 7-limit harmonies in a piece of music, along with the tuning most likely intended by the composer, there is little hard evidence that can be presented.
the only thing which i *can* document is that the "standard" tunings in Europe historically followed a rough trend from more to->less tempering of the "5th", i.e., from 19edo to 12edo (as in mousing-over from the bottom of the list in my applet, to the top).
as meantone tuning moved further and further away from 1/4-comma and 31edo (which gives a very good 4:5:6:7) and simultaneously closer and closer to 12edo (with its mediocre 5:4 and lousy 7:4), ratios of 7 seem to have generally fallen more and more out of favor.
there were always advocates of 7, but mainstream music-theory of the 1700s-1900s didn't admit it as an implied prime-factor in the harmony.
during the later 1800s there was quite a flurry of activity in microtonal experimentation, particularly in England and Germany, and particularly concerned with encompassing the ratios of 7 in harmony. but it was Partch who really opened the door to the higher-prime factors of 7 and 11.
now of course, i've presented the Euro-centric view here. in folk music from all over the world, in particular the Turkish/Persian/Arab music, i hear lots of intervals resembling 7- and 11-limit ratios.
Hello ALL,
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
