The tritriadic scale with Major Triads (1/1 5/4 3/2) on the Tonic (1/1), Subdominant (4/3) and Dominant (3/2) degrees.
The major-scale is a type of scale called "diatonic", an ancient Greek term meaning "thru tones", expressing the idea that the scale contains mostly "whole-steps" (that is, "tones") between the notes, which in the ancient pythagorean tuning are the ratio 9:8 (approximately 204 cents). However, all diatonic scales (that is: major, minor, and the other modes) contain a variety of step-sizes, generally two different ones but sometimes three, the largest of which may be designated "L" and the smallest by "s". Some diatonic scales also have an intermediate size which can be called "m", but the major-scale contains only two step-sizes (L and s).
All diatonic scales assume the 2:1 ratio ("octave", 1200 cents), or a close approximation to it, as an equivalence-interval. The scale is thus given in a "reference octave", generally in the range near middle-C, and all notes are considered to be "pitch-classes" which have pitches equivalent to them, with the same nominals (letter-names), in other octaves. The diatonic scales are all "heptatonic" (7-tone), which means that they contain 7 different notes, and an 8th note ("octave") which repeats the starting note -- an octave higher in the ascending form of the scale, or an octave lower in the descending form. The major-scale contains 7 "whole-steps" and 2 "half-steps", in this particular order: L L s L L L s. With the degrees of the major-scale numbered from 1 to 8, the L/s pattern is as follows, showing that "s" is the step-size between degrees 3 & 4 and 7 & 8 and "L" is the step-size everywhere else:
1 2 3 4 5 6 7 8 \_/ \_/ \/ \_/ \_/ \_/ \/ L L s L L L s
As with most music-theory introductions, we may use the major-scale based on "C" to illustrate, since the L/s pattern produces a scale in which all 7 of the different notes use only the nominals (letter-names) with no accidentals (flats or sharps) involved, and also since all 7 notes of the scale may be found on the white keys of the standard piano keyboard, thus keeping the presentation in its simplest form. Here is the C-major scale, irrespective of any particular tuning, as it appears in the standard pythagorean/meantone-based staff-notation in the treble clef:
The L/s pattern of step sizes in C-major is as follows:
C D E F G A B C \_/ \_/ \/ \_/ \_/ \_/ \/ L L s L L L s
(Note that the logical flaw in staff notation is a result of the two "s" steps between B:C and E:F having exactly the same appearance as all of the "L" steps between the other notes. This is because staff-notation was developed as a means of notating the diatonic scales, with not enough thought put into the fact that the steps are of two different sizes.)
The various versions of the major scale given in Chalmers's definition above are differentiated by their tunings, and may be illustrated as follows:
We begin here with the 12-edo version of the major-scale because it is probably the most familiar. Here is an illustration of the 12-edo major-scale based on "C", on the standard ("Halberstadt") piano keyboard; the 12-edo degree numbers label each key within the octave, and the 7 nominals (letter-names) designating the major-scale are labeled at the bottom of the white keys within that same octave; the staff-notation is given alongside, with the 12-edo degrees labeled:
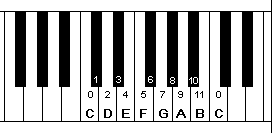
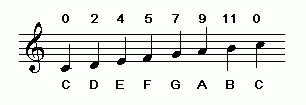
Note that in 12-edo tuning, the "whole-step" (L) is exactly twice the size of the "half-step" (s), exactly 200 and 100 cents respectively. Easley Blackwood's "R" ratio defines this relationship, and so in 12-edo, R=2.
The 3-limit pythagorean tuning of the major scale is historically important, being the version of the major scale which evolved first in Western music-theory, as a result of the process of "tuning by concords".
We may view this chain-of-5ths tuning on a 1-dimensional (i.e., linear) lattice-diagram, ignoring prime-factor 2 because it represents the equivalence-interval and plotting each note of the scale according to exponents of prime-factor 3. A small interval near the origin which may be used as a unison-vector is the "apotome", the pythagorean chromatic semitone, shown as 7 steps on the lattice:
interval name prime-factor 2,3-monzo ratio ~cents apotome 37 [* -5, > 2187/2048 113.6850061
The periodicity-block formed by this interval contains the 7-tone diatonic scale, indicated on this lattice as the set of pitches from F 3-4 to B 32. The chromatic semitone, a distance of 7 steps on the lattice, indicates a change from a plain letter-name to one with a sharp or a flat.
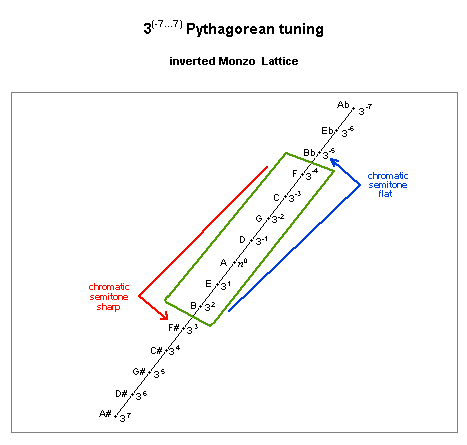
Analysis of the two step-sizes (L and s) of the pythagorean major-scale shows:
interval name prime-factor 2,3-monzo ratio ~cents
L tone 32 [* 2, > 9/8 203.9100017
s limma 3-5 [* -5, > 256/243 90.22499567 cents
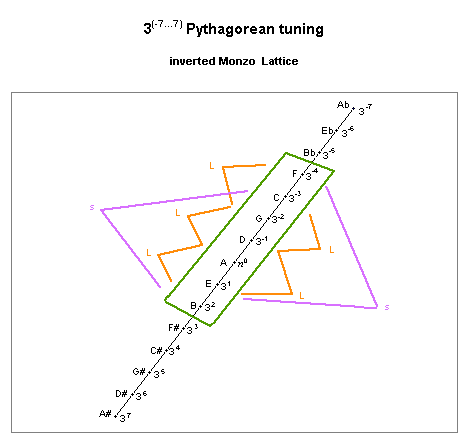
Note that the unison-vector defining the diatonic scale is also the difference between the two step sizes in that scale.
The pythagorean major-scale is notated below in staff-notation, with the ratios labeled above the notes:
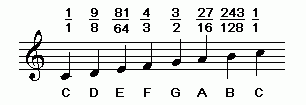
In the pythagorean tuning of the major-scale, the R = approximately 2.26 -- that is, the "whole-step" (L) is about 21/4 the size of the "half-step" (s).
The 5-limit just intonation tuning of the major scale is also historically important, because during the 1400s European music-theorists replaced three of the pythagorean ratios (those for "E", "A", and "B" in the C-major scale) with three which contained 5 as a prime-factor, and which are a syntonic-comma (ratio 81:80 = ~21.5 cents) smaller and have a softer, "sweeter", and more concordant sound than their pythagorean counterparts. This 5-limit major-scale is notated below in staff-notation, with the ratios labeled above the notes:
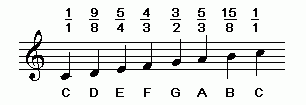
In the 5-limit JI tuning of the major-scale, the "half-step" ("s") is ratio 16:15, approximately 112 cents, and significantly larger than in both the 12-edo and the pythagorean tunings. Note that in JI there are two different sizes of "whole-step": one with ratio 9:8 (approximately 204 cents, the same as in pythagorean tuning), and another smaller one with ratio 10:9 (approximately 182 cents). If we label the larger "whole-step" as "L", the smaller "whole-step" as "L'" (for "L-prime"), the logarithmic L:s ratio is approximately 1.825, and the ratio of L':s is approximately 1.633. Note that the smaller whole-step should not be labeled "m" as it is not considered to be a different step-size in the scale's structure, but rather simply a different version of "L".
C D E F G A B C \_/ \_/ \/ \_/ \_/ \_/ \/ L L' s L L' L s
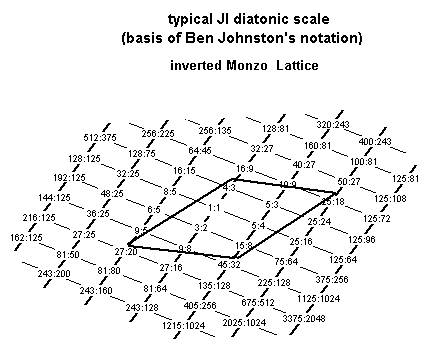
The unison-vectors which define this scale as a periodicity-block are the syntonic comma of ratio 81:80 = 2,3,5-monzo [-4 4 -1 > (which is acting here as the commatic unison-vector) and the ratio 25:24 = [-3 -1 2 > (which is acting here as the chromatic unison-vector). These unison-vectors are drawn here as the solid lines forming a parallelogram, which encloses the points which represent the ratios of the scale.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.