A term coined in July 2003 by a group of tuning theorists (including Aaron Hunt, Gene Ward Smith, and Joe Monzo), to describe one of a family of terms referring to units of resolution in MIDI tuning, used in electronic music software and computer music software. The prefix specifies the exponent of 2 which describes the number of MIDI tuning units per semitone, and the final "mu" is an acronym for "MIDI unit". In this work the numerical figure is used in preference to the verbal prefix.
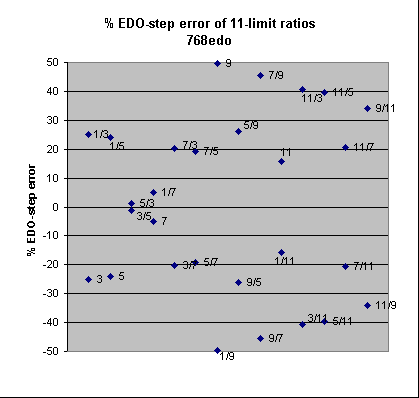
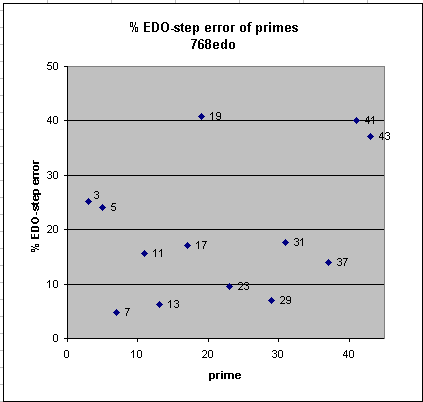
At the setting for 6mu pitch-bend resolution, a semitone is divided into 26 = 64 pitch-bend units. Thus there are 64 * 12 = 768 6mus in an "octave", so the 6mu measurement system may be thought of as 768-edo tuning, with a 6mu being one degree in 768-edo.
A 6mu is calculated as the 768th root of 2 -- 768√2, or 2(1/768) -- with a ratio of approximately 1:1.000902943. It is an irrational number, but is extremely close to the ratio 2217:2215 ( 31 5-1 443-1 7391 ):: the difference is ~ 1/70,000 of a cent, which for all intents and purposes makes the 6mu identical to that ratio. The formula for calculating the 6mu-value of any ratio is: 6mus = log10r * [ (26 * 12) / log10(2)] or 6mus = log2r * (26 * 12) , where r is the ratio.
A 6mu is:
The internal data structure of the 6mu requires one byte, with the first two bits reserved as flags, one to indicate the byte's status as data, and one to indicate the sign (+ or -) showing the direction of the pitch-bend up or down, and all six of the remaining bits used for the tuning data, as follows:
let "d" designate the bits that cannot be used
because it is reserved for the SysEx flag, to
indicate that this is a byte of pitch-bend data.
let "s" designate the bit that represents the
sign of the pitch-bend data, + or - .
let "x" designate unused bits
the 6mu spec thus uses a total of 2+6 = 8 bits.
thus, the maximum possible value is:
ds11 1111 [binary]
= +/- 3F [hex]
= +/- 63 [decimal]
note that the first nibble can only indicate the sign + or -
and the data-values 0, 16, 32, or 48 [decimal].
Below is an illustration of exactly how this works.
The "x" represents the status flag at the beginning of the byte, and is not recognized as part of the tuning resolution. The bit which represents 64 [decimal] is the sign bit. The actual tuning data begins with the bit representing 32 [decimal]. x 64 32 16 8 4 2 1 -- decimal value x 1 0 0 0 0 0 0 -- bits = 64 decimal = 40 hex = the plain MIDI-note, 0 cents deviation from 12edo. x 64 32 16 8 4 2 1 -- decimal value x 1 0 0 0 0 0 1 -- bits = 65 decimal = 41 hex = one unit (1.5625 cents) above the 12edo MIDI-note. x 64 32 16 8 4 2 1 -- decimal value x 0 1 1 1 1 1 1 -- bits = 63 decimal = 3F hex = one unit (1.5625 cents) below the 12edo MIDI-note.
Therefore the 6mu gives a range of possible values +/- as follows:
-------- bits --------- ------- cents ------
x 64 32 16 8 4 2 1 decimal hex decimal fraction
(128 80 +100.0000 +100)
x 1 1 1 1 1 1 1 127 7F + 98.4375 + 98 7/16
x 1 1 1 1 1 1 0 126 7E + 96.8750 + 96 14/16
x 1 1 1 1 1 0 1 125 7D + 95.3125 + 95 5/16
x 1 1 1 1 1 0 0 124 7C + 93.7500 + 93 12/16
x 1 1 1 1 0 1 1 123 7B + 92.1875 + 92 3/16
x 1 1 1 1 0 1 0 122 7A + 90.6250 + 90 10/16
x 1 1 1 1 0 0 1 121 79 + 89.0625 + 89 1/16
x 1 1 1 1 0 0 0 120 78 + 87.5000 + 87 8/16
x 1 1 1 0 1 1 1 119 77 + 85.9375 + 85 15/16
x 1 1 1 0 1 1 0 118 76 + 84.3750 + 84 6/16
x 1 1 1 0 1 0 1 117 75 + 82.8125 + 82 13/16
x 1 1 1 0 1 0 0 116 74 + 81.2500 + 81 4/16
x 1 1 1 0 0 1 1 115 73 + 79.6875 + 79 11/16
x 1 1 1 0 0 1 0 114 72 + 78.1250 + 78 2/16
x 1 1 1 0 0 0 1 113 71 + 76.5625 + 76 9/16
x 1 1 1 0 0 0 0 112 70 + 75.0000 + 75
x 1 1 0 1 1 1 1 111 6F + 73.4375 + 73 7/16
x 1 1 0 1 1 1 0 110 6E + 71.8750 + 71 14/16
x 1 1 0 1 1 0 1 109 6D + 70.3125 + 70 5/16
x 1 1 0 1 1 0 0 108 6C + 68.7500 + 68 12/16
x 1 1 0 1 0 1 1 107 6B + 67.1875 + 67 3/16
x 1 1 0 1 0 1 0 106 6A + 65.6250 + 65 10/16
x 1 1 0 1 0 0 1 105 69 + 64.0625 + 64 1/16
x 1 1 0 1 0 0 0 104 68 + 62.5000 + 62 8/16
x 1 1 0 0 1 1 1 103 67 + 60.9375 + 60 15/16
x 1 1 0 0 1 1 0 102 66 + 59.3750 + 59 6/16
x 1 1 0 0 1 0 1 101 65 + 57.8125 + 57 13/16
x 1 1 0 0 1 0 0 100 64 + 56.2500 + 56 4/16
x 1 1 0 0 0 1 1 99 63 + 54.6875 + 54 11/16
x 1 1 0 0 0 1 0 98 62 + 53.1250 + 53 2/16
x 1 1 0 0 0 0 1 97 61 + 51.5625 + 51 9/16
x 1 1 0 0 0 0 0 96 60 + 50.0000 + 50
x 1 0 1 1 1 1 1 95 5F + 48.4375 + 48 7/16
x 1 0 1 1 1 1 0 94 5E + 46.8750 + 46 14/16
x 1 0 1 1 1 0 1 93 5D + 45.3125 + 45 5/16
x 1 0 1 1 1 0 0 92 5C + 43.7500 + 43 12/16
x 1 0 1 1 0 1 1 91 5B + 42.1875 + 42 3/16
x 1 0 1 1 0 1 0 90 5A + 40.6250 + 40 10/16
x 1 0 1 1 0 0 1 89 59 + 39.0625 + 39 1/16
x 1 0 1 1 0 0 0 88 58 + 37.5000 + 37 8/16
x 1 0 1 0 1 1 1 87 57 + 35.9375 + 35 15/16
x 1 0 1 0 1 1 0 86 56 + 34.3750 + 34 6/16
x 1 0 1 0 1 0 1 85 55 + 32.8125 + 32 13/16
x 1 0 1 0 1 0 0 84 54 + 31.2500 + 31 4/16
x 1 0 1 0 0 1 1 83 53 + 29.6875 + 29 11/16
x 1 0 1 0 0 1 0 82 52 + 28.1250 + 28 2/16
x 1 0 1 0 0 0 1 81 51 + 26.5625 + 26 9/16
x 1 0 1 0 0 0 0 80 50 + 25.0000 + 25
x 1 0 0 1 1 1 1 79 4F + 23.4375 + 23 7/16
x 1 0 0 1 1 1 0 78 4E + 21.8750 + 21 14/16
x 1 0 0 1 1 0 1 77 4D + 20.3125 + 20 5/16
x 1 0 0 1 1 0 0 76 4C + 18.7500 + 18 12/16
x 1 0 0 1 0 1 1 75 4B + 17.1875 + 17 3/16
x 1 0 0 1 0 1 0 74 4A + 15.6250 + 15 10/16
x 1 0 0 1 0 0 1 73 49 + 14.0625 + 14 1/16
x 1 0 0 1 0 0 0 72 48 + 12.5000 + 12 8/16
x 1 0 0 0 1 1 1 71 47 + 10.9375 + 10 15/16
x 1 0 0 0 1 1 0 70 46 + 9.3750 + 9 6/16
x 1 0 0 0 1 0 1 69 45 + 7.8125 + 7 13/16
x 1 0 0 0 1 0 0 68 44 + 6.2500 + 6 4/16
x 1 0 0 0 0 1 1 67 43 + 4.6875 + 4 11/16
x 1 0 0 0 0 1 0 66 42 + 3.1250 + 3 2/16
x 1 0 0 0 0 0 1 65 41 + 1.5625 + 1 9/16
x 1 0 0 0 0 0 0 64 40 0.0000 0
x 0 1 1 1 1 1 1 63 3F - 1.5625 - 1 9/16
x 0 1 1 1 1 1 0 62 3E - 3.1250 - 3 2/16
x 0 1 1 1 1 0 1 61 3D - 4.6875 - 4 11/16
x 0 1 1 1 1 0 0 60 3C - 6.2500 - 6 4/16
x 0 1 1 1 0 1 1 59 3B - 7.8125 - 7 13/16
x 0 1 1 1 0 1 0 58 3A - 9.3750 - 9 6/16
x 0 1 1 1 0 0 1 57 39 - 10.9375 - 10 15/16
x 0 1 1 1 0 0 0 56 38 - 12.5000 - 12 8/16
x 0 1 1 0 1 1 1 55 37 - 14.0625 - 14 1/16
x 0 1 1 0 1 1 0 54 36 - 15.6250 - 15 10/16
x 0 1 1 0 1 0 1 53 35 - 17.1875 - 17 3/16
x 0 1 1 0 1 0 0 52 34 - 18.7500 - 18 12/16
x 0 1 1 0 0 1 1 51 33 - 20.3125 - 20 5/16
x 0 1 1 0 0 1 0 50 32 - 21.8750 - 21 14/16
x 0 1 1 0 0 0 1 49 31 - 23.4375 - 23 7/16
x 0 1 1 0 0 0 0 48 30 - 25.0000 - 25
x 0 1 0 1 1 1 1 47 2F - 26.5625 - 26 9/16
x 0 1 0 1 1 1 0 46 2E - 28.1250 - 28 2/16
x 0 1 0 1 1 0 1 45 2D - 29.6875 - 29 11/16
x 0 1 0 1 1 0 0 44 2C - 31.2500 - 31 4/16
x 0 1 0 1 0 1 1 43 2B - 32.8125 - 32 13/16
x 0 1 0 1 0 1 0 42 2A - 34.3750 - 34 6/16
x 0 1 0 1 0 0 1 41 29 - 35.9375 - 35 15/16
x 0 1 0 1 0 0 0 40 28 - 37.5000 - 37 8/16
x 0 1 0 0 1 1 1 39 27 - 39.0625 - 39 1/16
x 0 1 0 0 1 1 0 38 26 - 40.6250 - 40 10/16
x 0 1 0 0 1 0 1 37 25 - 42.1875 - 42 3/16
x 0 1 0 0 1 0 0 36 24 - 43.7500 - 43 12/16
x 0 1 0 0 0 1 1 35 23 - 45.3125 - 45 5/16
x 0 1 0 0 0 1 0 34 22 - 46.8750 - 46 14/16
x 0 1 0 0 0 0 1 33 21 - 48.4375 - 48 7/16
x 0 1 0 0 0 0 0 32 20 - 50.0000 - 50
x 0 0 1 1 1 1 1 31 1F - 51.5625 - 51 9/16
x 0 0 1 1 1 1 0 30 1E - 53.1250 - 53 2/16
x 0 0 1 1 1 0 1 29 1D - 54.6875 - 54 11/16
x 0 0 1 1 1 0 0 28 1C - 56.2500 - 56 4/16
x 0 0 1 1 0 1 1 27 1B - 57.8125 - 57 13/16
x 0 0 1 1 0 1 0 26 1A - 59.3750 - 59 6/16
x 0 0 1 1 0 0 1 25 19 - 60.9375 - 60 15/16
x 0 0 1 1 0 0 0 24 18 - 62.5000 - 62 8/16
x 0 0 1 0 1 1 1 23 17 - 64.0625 - 64 1/16
x 0 0 1 0 1 1 0 22 16 - 65.6250 - 65 10/16
x 0 0 1 0 1 0 1 21 15 - 67.1875 - 67 3/16
x 0 0 1 0 1 0 0 20 14 - 68.7500 - 68 12/16
x 0 0 1 0 0 1 1 19 13 - 70.3125 - 70 5/16
x 0 0 1 0 0 1 0 18 12 - 71.8750 - 71 14/16
x 0 0 1 0 0 0 1 17 11 - 73.4375 - 73 7/16
x 0 0 1 0 0 0 0 16 10 - 75.0000 - 75
x 0 0 0 1 1 1 1 15 0F - 76.5625 - 76 9/16
x 0 0 0 1 1 1 0 14 0E - 78.1250 - 78 2/16
x 0 0 0 1 1 0 1 13 0D - 79.6875 - 79 11/16
x 0 0 0 1 1 0 0 12 0C - 81.2500 - 81 4/16
x 0 0 0 1 0 1 1 11 0B - 82.8125 - 82 13/16
x 0 0 0 1 0 1 0 10 0A - 84.3750 - 84 6/16
x 0 0 0 1 0 0 1 9 09 - 85.9375 - 85 15/16
x 0 0 0 1 0 0 0 8 08 - 87.5000 - 87 8/16
x 0 0 0 0 1 1 1 7 07 - 89.0625 - 89 1/16
x 0 0 0 0 1 1 0 6 06 - 90.6250 - 90 10/16
x 0 0 0 0 1 0 1 5 05 - 92.1875 - 92 3/16
x 0 0 0 0 1 0 0 4 04 - 93.7500 - 93 12/16
x 0 0 0 0 0 1 1 3 03 - 95.3125 - 95 5/16
x 0 0 0 0 0 1 0 2 02 - 96.8750 - 96 14/16
x 0 0 0 0 0 0 1 1 01 - 98.4375 - 98 7/16
x 0 0 0 0 0 0 0 0 00 -100.0000 -100
For practical use in tuning MIDI-files, an interval's semitone value must first be calculated. The nearest integer semitone is translated into a MIDI note-number (which can generally also be described by letter-name plus optional accidental: A, Bb, C#, etc., followed by an "octave" register-number, as A-1, Bb2, etc.). Then the remainder or deficit is converted into 6mus plus or minus, respectively.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.