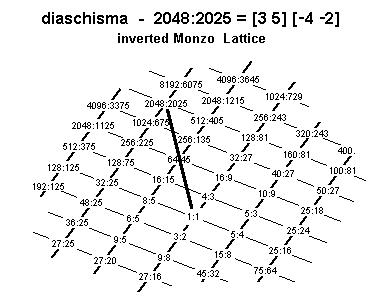
The diaschisma is a small interval composed of 2 major-3rds down and 4 perfect-5ths down = 2113-45-2, also expressed as the 2,3,5-monzo [11 -4, -2 > .
Its ratio is 2048/2025 [= 0.20 Semitones = ~19.55256881 or ~195/9 cents].
The term was used by Alexander Ellis in his English translation of Helmholtz, On the Sensations of Tone (1875). It had been referred to earlier by Rameau (Traité de l'harmonie, 1722) as the "diminished comma".
Monzo, 5-limit intervals, 100 cents and under suggests calling this the "sub-bipental comma" to explicitly indicate the exponent of 5.
Below is a Monzo lattice illustrating the prime factorization of the diaschisma:
Graham Breed gives an excellent summary of Diaschismic Scales, temperaments based on the diaschisma.
The standard epimoric approximation to the diaschisma is the ratio 89:88 ( = ~19.56217479 cents), whose 2,3,5,11,89-monzo is | -3, 0, 0, -1, 1 > .
The small difference between them is:
-------- monzo --------
2 3 5 11 89
| -3 0 0 -1 1 > = epimoric approximation, 89:88 ratio
- | 11 -4 -2 0 0 > = actual diaschisma, 2048:2025 ratio
--------------------------
|-14 4 2 -1 1 > = 180225:180224 ratio = ~0.009605986 cent ( = ~1/100 cent)
Tuning treatises before c.1970 sometimes defined the diaschisma as the 89:88 ratio without emphasis on the fact of its being an approximation, particularly in the German literature of c.1850-1950. A good example is Helmholtz in On the Sensations of Tone....
The earliest theorist known to have used the term "diaschisma" is Philolaus (Greek, c.400s BC), whose work survives only in a commentary on it by Boethius. He employed it to refer to an integral logarithmic half of a diesis (which for him was the diatonic semitone, the smaller of the two semitones in pythagorean tuning, and later called limma).
Its ratio is is (28 3-5)(1/2) = ~45.11249784 cents; the 2,3-rational-monzo is [ -4 -5/2 > . This interval was called the enharmonic diesis by Aristoxenos, who only measured it aurally.
Johannes Tinctoris, in his Expositio manus ["exposition of the hand", c.1475], uses diaschisma with the same meaning as Philolaus.
In actual practice in Tinctoris's day (and possibly in Philolaus's too), this interval would have been calculated from an extended pythagorean chain as two pythagorean commas = 324 = ~46.92002077 cents. In this calculation, two diaschismata = 348 = ~93.84004154 cents, which is one mercator comma (= ~33/5cents) larger than the true "minor semitone" 3-5 = ~90.22499567 cents. The mercator comma would have been considered a negligible difference, thus the equivocation invoked by Tinctoris.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.