@ 00 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Login   |  Encyclopedia Index

A gentle introduction to
Fokker periodicity blocks: an excursion

[from Monzo: This exposition provides information useful for understanding my concept of finity.]

previous installment (part 2)

In this excursion I aim to demonstrate that there is nothing sacred about the parallelogram shape for periodicity blocks and other shapes are equally valid.

Let's take the lattice diagram from "A gentle introduction to Fokker periodicity blocks, part 2", specifically the one in which we found the JI minor scale within the parallelogram defined by the matrix

( 4 -1)
(     )
(-1  2)
		

[see the original parallelogram.]

The meaning of the periodicity block is preserved if we take any part of it and transpose it by a unison vector. The resulting shape will still tile the plane, contain one pitch from each equivalence class, and have area equal to the determinant of the matrix. Now let's say we feel that the parallelogram shape is too "pointy". We can divide the bottom-right "point" of each parallelogram into two triangular wedges, as shown below.

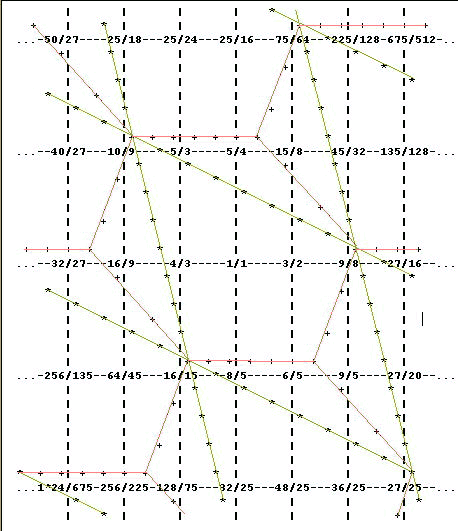
Now take the "right" wedge of each pair and transpose it by (-4 1), a negative syntonic comma. Take the "bottom" wedge of each pair and transpose it by (-1 2), a chromatic semitone. Now the periodicity blocks look like this:

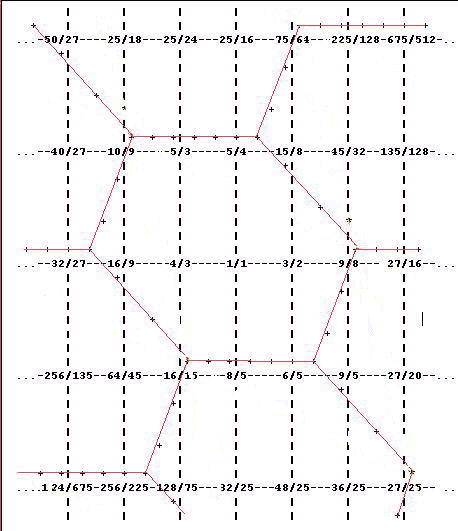
Now the periodicity blocks are hexagonal, and form a honeycomb arrangement. The scale that happens to fall within the hexagon with 1/1 in it is the standard Indian diatonic scale, with 4/3 as the tonic (in other words, shift the hexagon one step to the right to get the usual ratios: 1/1 9/8 5/4 4/3 3/2 27/16 15/8). But the position of the hexagon is arbitrary and other types of diatonic scale, including our "JI major scale" could fit inside it. The differences in shape between parallelograms and hexagons become more important as the unison vectors become longer, more notes fall inside the periodicity blocks, and the shape of the border is more clearly implied by the configuration of notes within it.

We noted before that the parallelogram-shaped periodicity blocks were everywhere one unison vector wide in the direction of each of the two unison vectors. The hexagonal periodicity blocks are one unison vector wide through the middle two-thirds of their area, and are thinner than that at the extremes. This property is respected not only for the two unison vectors, but also for an additional vector, (3 1), a "greater limma" or 92 cents. This vector is the sum of the two unison vectors: (4 -1) + (-1 2) = (3 1) (yes, vector addition is that obvious). Now the hexagonal blocks are symmetrical with respect to these three vectors. In fact we could have constructed these hexagonal blocks the same way had we started with a parallelogram based on defining any two of these three vectors as the unison vectors. Such a redefinition can never change the area of the periodicity block:

|a     b|                                                           |a  b|
|       | = a*(d+b) - b*(c+a) = a*d + a*b - b*c - b*a = a*d - b*c = |    |
|c+a d+b|                                                           |c  d|
		

Upon such a substitution, the third vector of the hexagon will be the difference instead of the sum of the unison vectors -- in some cases the hexagon which treats the difference, rather than the sum, of the unison vectors symmetrically with the unison vectors themselves will be more effective in making the periodicity block less pointy. The difference, like the sum, can substitute for one of the unison vectors without changing the area of the block:

|a     b|                                                           |a  b|
|       | = a*(d-b) - b*(c-a) = a*d - a*b - b*c + b*a = a*d - b*c = |    |
|c-a d-b|                                                           |c  d|
		

Let's try constructing hexagonal periodicity blocks for our other 5-limit matrix;

(4 -1)
(    )
(0 -3)
		

First, we'll divide the upper-left "point" of each parallelogram into two wedges:

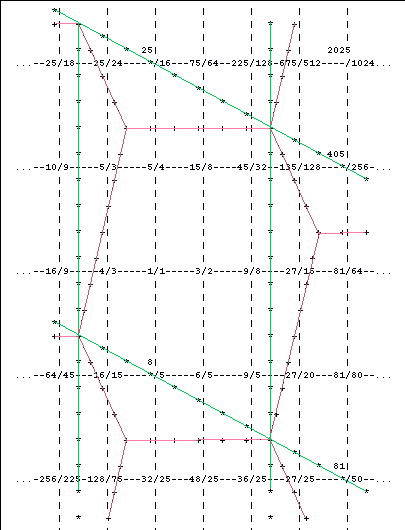
Now take the "upper" wegde of each pair and transpose it by (0 -3), and take the "left" wedge of each pair and transpose it by (4 -1). We end up with this pattern:

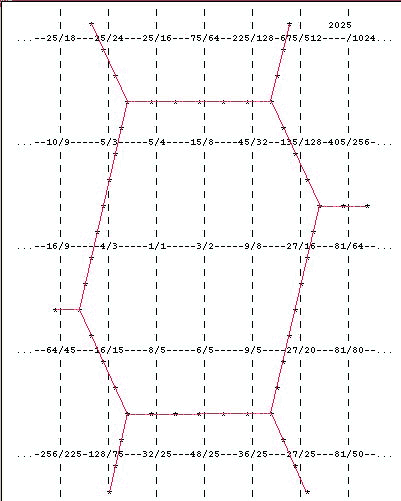
The 12-tone scale that happens to fall within the hexagon with 1/1 in it is the Modern Indian Gamut. The "new" vector that is treated symmetrically with the unison vectors is their sum, (4 2), a diaschisma or 20 cents.

I hope this excursion was interesting (I came up with the idea of hexagonal periodicity blocks last night, inspired in part by my discussions here with Kees van Prooijen) and I'll move on to 3-D periodicity blocks next time.

next (and final) installment