72-ed2 / 72-edo / 72-ET / 72-tone equal-temperament
The tuning determined by 72 logarithmically equal divisions of the "octave" (see also EDO).
72-edo has been advocated as a tuning by Ivan Wyschnegradsky in Paris, by Franz Richter Herf in Austria, by Rick Tagawa in California, and by Ezra Sims, Joe Maneri, and many other Boston-area microtonalists (see Ted Mook's 72-tET Finale font), as an easily-grasped representation of the virtual pitch continuum.
72-edo has been advocated as a notation capable of giving good representations of just-intonation pitches by many tuning theorists. Paul Erlich has argued powerfully and eloquently for its use in many posts to the internet Tuning List. It is also the superset which contains within it several subset tunings from a nearly optimal version of the miracle family of temperaments.
Before describing Monzo's notation in greater detail, it should be noted that several other tuning theorists adopted an ASCII standard in 2001 which differs from Monzo's in that it more closely resembles the Sims/Maneri symbols which are actually used in scores. (Monzo uses exactly the same symbols in both email and scores.) The two notations are identical in terms of how they operate; only in one case different symbols are used and in another the symbols are distributed differently.
Below are the legends for the intonational inflections of the accidental symbols for each system, so that in reading what follows below, one need merely consult the legends to make the comparison between the two notations.
Tuning list standard, based on Sims/Maneri 72edo notation lower raise inflection cents b # semitone 100 ] [ 1/4-tone 50 < > 1/6-tone 331/3 v ^ 1/12-tone 162/3
Monzo 72-edo HEWM notation lower raise inflection cents b # semitone 100 v ^ 1/4-tone 50 < > 1/6-tone 331/3 - + 1/12-tone 162/3
Continuing only in Monzo's HEWM notation, below is a table of the range of the virtual pitch continuum which can be represented by each 72-edo note. I cover only one semitone, as it can be reproduced similarly for the other 11.
The table gives the absolute Semitone ranges (i.e., cents as a fraction of semitones), the nearest 12-edo degree and its cents deviation (i.e., to relate 72-edo to Johnny Reinhard's 1200-edo notation), and MIDI pitch-bend values for the deviation from 12-edo.
This emphasizes the use of 72-edo as a notation, rather than as an actual tuning. (The latter would give the precise cent or pitch-bend value of each 72-edo degree, which I give further below.)
This is how 72-edo can be used to represent pitches which are expected to actually be tuned slightly differently, whether just-intonation, other (or poly-) EDOs, or otherwise.
nearest Semitones MIDI
12-edo deviation pitch-bend
Semitones degree from 12-edo (12mus)
1.08 1 + 0.08 + 341
12 C# < >
0.92 1 - 0.08 - 341
10 C#- < >
0.75 1 - 0.25 - 1024
8 C#< < >
0.58 1 - 0.42 - 1727
6 C^ or C#v < >
0.42 0 + 0.42 + 1727
4 C> < >
0.25 0 + 0.25 + 1024
2 C+ < >
0.08 0 + 0.08 + 341
0 C < >
-0.08 0 - 0.08 - 341
72-edo is calculated by taking the 72nd root of each successive power of 2, from 0 to 71, with higher or lower "octaves" of these 12 notes assumed to be, and tuned as, equivalents. The basic step-size is 16 & 2/3 cents.
Below is an overview of the complete 72-edo scale as a tuning. Notes which are presented horizontally adjacent are enharmonically equivalent.
72-edo Monzo ASCII adaptation of Sims/Herf notation
8 different symbols in addition to the letter-names:
+ < ^ #
- > v b
16&2/3¢ 33&1/3¢ 50¢ 100¢
1/12 1/6 1/4 1/2 of a 12-edo "tone"
DE- SEMI- /-------------- NOTATION ------------------\
GREE TONES
0 0.00 C
===========================================================
71 11.83 C-
-----------------------------------------------------------
70 11.67 C<
-----------------------------------------------------------
69 11.50 Cv B^
-----------------------------------------------------------
68 11.33 B>
-----------------------------------------------------------
67 11.17 B+
-----------------------------------------------------------
66 11.00 (Cb) B (Ax)
===========================================================
65 10.83 B-
-----------------------------------------------------------
64 10.67 B<
-----------------------------------------------------------
63 10.50 Bv (Bb^ A#^)
-----------------------------------------------------------
62 10.33 Bb> A#>
-----------------------------------------------------------
61 10.17 Bb+ A#
-----------------------------------------------------------
60 10.00 Bb A#
===========================================================
59 9.83 Bb- A#-
-----------------------------------------------------------
58 9.67 Bb< A#<
-----------------------------------------------------------
57 9.50 (Bbv A#v) A^
-----------------------------------------------------------
56 9.33 A>
-----------------------------------------------------------
55 9.17 A+
-----------------------------------------------------------
54 9.00 (Bbb) A (Gx)
===========================================================
53 8.83 A-
-----------------------------------------------------------
52 8.67 A<
-----------------------------------------------------------
51 8.50 Av (Ab^ G#^)
-----------------------------------------------------------
50 8.33 Ab> G#>
-----------------------------------------------------------
49 8.17 Ab+ G#+
-----------------------------------------------------------
48 8.00 Ab G#
===========================================================
47 7.83 Ab- G#-
-----------------------------------------------------------
46 7.67 Ab< G#<
-----------------------------------------------------------
45 7.50 (Abv G#v) G^
-----------------------------------------------------------
44 7.33 G>
-----------------------------------------------------------
43 7.17 G+
-----------------------------------------------------------
42 7.00 (Abb Fx) G
===========================================================
41 6.83 G-
-----------------------------------------------------------
40 6.67 G<
-----------------------------------------------------------
39 6.50 (F#^) Gv (Gb^)
-----------------------------------------------------------
38 6.33 F#> Gb>
-----------------------------------------------------------
37 6.17 F#+ Gb+
-----------------------------------------------------------
36 6.00 F# Gb
===========================================================
35 5.83 F#- Gb-
-----------------------------------------------------------
34 5.67 F#< Gb<
-----------------------------------------------------------
33 5.50 (F#v) F^ (Gbv)
-----------------------------------------------------------
32 5.33 F>
-----------------------------------------------------------
31 5.17 F+
-----------------------------------------------------------
30 5.00 (E#) F
===========================================================
29 4.83 F-
-----------------------------------------------------------
28 4.67 F<
-----------------------------------------------------------
27 4.50 E^ Fv
-----------------------------------------------------------
26 4.33 E>
-----------------------------------------------------------
25 4.17 E+
-----------------------------------------------------------
24 4.00 (Dx) E (Fb)
===========================================================
23 3.83 E-
-----------------------------------------------------------
22 3.67 E<
-----------------------------------------------------------
21 3.50 (D#^ Eb^) Ev
-----------------------------------------------------------
20 3.33 D#> Eb>
-----------------------------------------------------------
19 3.17 D#+ Eb+
-----------------------------------------------------------
18 3.00 D# Eb
===========================================================
17 2.83 D#- Eb-
-----------------------------------------------------------
16 2.67 D#< Eb<
-----------------------------------------------------------
15 2.50 D^ (D#v Ebv)
-----------------------------------------------------------
14 2.33 D>
-----------------------------------------------------------
13 2.17 D+
-----------------------------------------------------------
12 2.00 (Cx) D (Ebb)
===========================================================
11 1.83 D-
-----------------------------------------------------------
10 1.67 D<
-----------------------------------------------------------
9 1.50 (C#^ Db^) Dv
-----------------------------------------------------------
8 1.33 C#> Db>
-----------------------------------------------------------
7 1.17 C#+ Db+
-----------------------------------------------------------
6 1.00 C# Db
===========================================================
5 0.83 C#- Db-
-----------------------------------------------------------
4 0.67 C#< Db<
-----------------------------------------------------------
3 0.50 C^ (C#v Dbv)
-----------------------------------------------------------
2 0.33 C>
-----------------------------------------------------------
1 0.17 C+
-----------------------------------------------------------
0 0.00 C
===========================================================
*************************************************
readily divided into smaller systems:
72-edo = (2^3)*(3^2) degrees
all possibilities of the matrix:
2^ 3^ # of degrees:
|1 0| = 2
|2 0| = 4
|3 0| = 8
|0 1| = 3
|1 1| = 6
|2 1| = 12
|3 1| = 24
|0 2| = 9
|1 2| = 18
|2 2| = 36
|3 2| = 72
arranged in order of number of degrees:
|1 0| = 2 tritone
|0 1| = 3 augmented triad
|2 0| = 4 diminished 7th tetrad
|1 1| = 6 whole tones
|3 0| = 8
|0 2| = 9
|2 1| = 12 semitones
|1 2| = 18 third-tones
|3 1| = 24 quarter-tones
|2 2| = 36 sixth-tones
|3 2| = 72 twelfth-tones
72-edo contains all these divisions within it.
Thus it subdivides into 10 smaller equal systems.
Paul Erlich has also pointed out that it should be emphasized how well 72-edo approximates several just-intonation tuning systems. His Yahoo Tuning List message 21486 gives a good summary of this. In brief, each 72-edo accidental represents an intonational inflection of one step along a prime-axis of the lattice, for primes up to 11.
Thus, + and - represent 1/12-tones, and signify an inflection of a syntonic-comma or an increase or decrease of one in the exponent of 5, which is the same as saying: one step along the 5-axis on the lattice.
< and > represent 1/6-tones, and signify an inflection of a septimal-comma or an increase or decrease of one in the exponent of 7, which is the same as saying: one step along the 7-axis on the lattice.
And ^ and v represent 1/4-tones, and signify an inflection of an undecimal diesis or an increase or decrease of one in the exponent of 11, which is the same as saying: one step along the 11-axis on the lattice.
I have also formulated a method of notating 72-edo simply on my quarter-tone staff paper. Below is shown the entire 72-edo scale and also representations of two segments of the harmonic series.

Here is a bit more than one "octave" of a mapping I designed to put 72-edo on the keyboard of the Starr Labs Ztar, showing the 72-edo degrees and my ASCII 72-edo notation. Here the pitches rise by one degree from "string" to "string", then continue at the bottom of the next "fret".
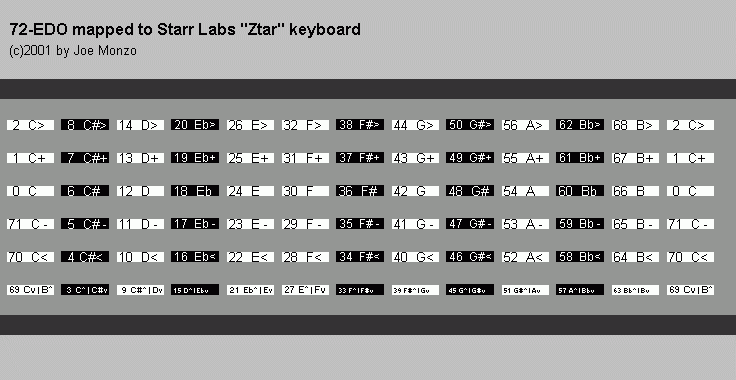
The quarter-tone pitches at the bottom of each column rightfully should be a different shade or color, because they fall in the boundary between the pitches that are mapped to the black and white keys. To me, the small size of the type on the quarter-tone keys (due to the inclusion of both of the enharmonic spellings for these pitches) served here to differentiate them enough from the other black and white keys.
Below is another mapping of 72-edo to the Ztar keyboard, which treats its array as a 5-limit lattice-diagram:

Invoking xenharmonic bridges which allow 5-limit pitches to be treated as higher-limit pitches, as described in Tuning List message 1372 (Mon Mar 8, 1999 1:25 am), one may obtain a comprehensive quasi-just 11-limit system.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by selecting the highest level of financial support that you can afford. Thank you.
