31-ed2 / 31-edo / 31-ET / 31-tone equal-temperament
31-tone equal-temperament in standard meantone notation

Below is a tabulation of approximate and exact cents values for 31-edo, arranged in descending scalar order:
31-edo
-- note name -- degree ~cents exact cents
C ............... 31 1200 1200
B# .. 30 1161.290323 1161 + 09/31
Cb .............. 29 1122.580645 1122 + 18/31
B ... 28 1083.870968 1083 + 27/31
Ax .... 27 1045.16129 1045 + 05/31
Bb .. 26 1006.451613 1006 + 14/31
A# .... 25 967.7419355 967 + 23/31
Bbb . 24 929.0322581 929 + 01/31
A ..... 23 890.3225806 890 + 10/31
Gx ...... 22 851.6129032 851 + 19/31
Ab .... 21 812.9032258 812 + 28/31
G# ...... 20 774.1935484 774 + 06/31
Abb ... 19 735.483871 735 + 15/31
G ....... 18 696.7741935 696 + 24/31
Fx ........ 17 658.0645161 658 + 02/31
Gb ...... 16 619.3548387 619 + 11/31
F# ........ 15 580.6451613 580 + 20/31
Gbb ..... 14 541.9354839 541 + 29/31
F ......... 13 503.2258065 503 + 07/31
E# .......... 12 464.516129 464 + 16/31
Fb ........ 11 425.8064516 425 + 25/31
E ........... 10 387.0967742 387 + 03/31
Dx ............ 9 348.3870968 348 + 12/31
Eb .......... 8 309.6774194 309 + 21/31
D# ............ 7 270.9677419 270 + 30/31
Ebb ......... 6 232.2580645 232 + 08/31
D ............. 5 193.5483871 193 + 17/31
Cx .............. 4 154.8387097 154 + 26/31
Db ............ 3 116.1290323 116 + 04/31
C# .............. 2 77.41935484 77 + 13/31
Dbb ........... 1 38.70967742 38 + 22/31
C ............... 0 0 0
Each equal-temperament belongs to several different temperament families, based on the particular promos which it tempers out. 31-edo is historically one of the most important, primarily because it is a member of the meantone family, and in particular because it closely resembles 1/4-comma meantone. Note that because 31-edo's cardinality is a prime-number, any of 31-edo's intervals may be used as a generator to generate the entire tuning.
31-edo as approximation of 1/4-comma meantone
Meantone temperaments are classified as "linear temperaments", and belong to the category of linear temperaments called "chain of 5ths" tunings, because they are analagous to the long-traditional pythagorean tuning, in that they use a generator which is a type of "perfect-5th", albeit one which is tempered so that its interval size is slightly smaller than the "pure" pythagorean "5th" (the pythagorean "5th" is ~702 cents). Using "C" as the name for the reference pitch, any "chain of 5ths" tuning (i.e., any tuning which uses a generator which is that tuning's version of the "perfect-5th") may be schematically illustrated as follows:
note names: Bb F C G D A E B F#
... --+---+---+---+---+---+---+---+---+-- ...
generator-5ths: -2 -1 0 +1 +2 +3 +4 +5 +6
As can be seen from the tabulation of 31-edo cents values above, the closest approximation to the pythagorean "5th" in 31-edo is given by 18 degrees of 31-edo, an interval with a ratio of ~1.495517882 and a logarithmic size of 696 + 24/31 (~696.7741935) cents.
All meantone tunings contain subsets which are diatonic scales consisting of two different "step" sizes, a "Large" and a "small", which may be designated L and s. In all meantone tunings, the large interval (L) is the "whole-step" or "whole-tone", the interval of a "major 2nd", and is found by traversing +2 generator "5ths" and reducing by 1 octave; thus, in 31-edo, the L is:
C = n0
first, stack 2 generator "5ths":
8ve gen ~ratio cents 31-edo degrees
2^(((18*gen)/31)+8ve)
G [ 0 +1] 1.495517882 696 + 24/31 18
+ 5th [ 0 +1] * 1.495517882 + 696 + 24/31 + 18
-------------- ------------- -------------- ----
D [ 0 +2] 2.236573736 1393 + 17/31 36 = 2 generator "5ths" (= major-9th)
then, reduce by 1 octave to normalize:
8ve gen ~ratio cents 31-edo degrees
2(((18*gen)/31)+8ve)
D [ 0 +2] 2.236573736 1393 + 17/31 36
- 8ve [ 1 0] ÷ 2 - 1200 - 31
-------------- ------------- -------------- ----
D [-1 +2] 1.118286868 193 + 17/31 5 = major-2nd = L
Here is another example, which uses notes derived from +1 and -1 generators, where the -1 generator has already been octave normalized:
C = n0
8ve gen ~ratio cents 31-edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
G [ 0 +1] 1.495517882 696 + 24/31 18
- F [+1 -1] ÷ 1.337329378 - 503 + 07/31 - 13
------------- ------------- --------------- ----
* [-1 +2] 1.118286868 193 + 17/31 5
* This always results in a change of letter-name.
This is the "mean-tone" which occurs almost exactly midway between the two just-intonation "whole-tones" with ratios of 10:9 and 9:8. (The exact mean-tone is that of 1/4-comma meantone.)
By continuing the process of stacking generators and normalizing, one may obtain the diatonic major scale. As an example, on the linear lattice-diagram illustrated above, the C-major scale appears as a subset of the lattice, between generators -1 and +5 inclusive. Regardless of the actual pitches (frequencies, or ratios, or cents values, etc.), the major scale whose tonic is the reference pitch (in this case, C) maps this way in any chain-of-5ths tuning.
In the table below, the "8ve" (octaves) and "gen" (generator 5ths) columns on the left show the generic [period, generator] mapping of pitches in the C-major scale for all members of the meantone family, and the "~ratio", "~cents", and "31-edo degrees" columns show the values associated with the mapping of the C-major scale specific to 31-edo:
C = n0
8ve gen ~ratio cents 31-edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
B [-2 5] 1.870243098 1083 + 27/31 28
A [-1 3] 1.672418009 890 + 10/31 23
G [ 0 1] 1.495517882 696 + 24/31 18
F [ 1 -1] 1.337329378 503 + 07/31 13
E [-2 4] 1.25056552 387 + 03/31 10
D [-1 2] 1.118286868 193 + 17/31 5
C [ 0 0] 1 0 0
(compare the "gen" values with those in the "chain of 5ths" linear lattice-diagram above)
In all meantone tunings, the small interval (s) is the "half-step", which is also the diatonic-semitone and the interval of a "minor 2nd", and is found by traversing -5 generator "5ths" (which is equivalent to +5 generator "4ths"). As can be seen in the "chain of 5ths" schematic above, this may be found twice in any major scale: between the octave above the tonic (reference note) and the leading-tone or major-7th, and also between the perfect-4th and the major-3rd. In 31-edo, the s is thus:
C = n0
s between octave and major-7th:
8ve gen ~ratio cents 31-edo degrees
2(((18*gen)/31)+8ve)
C [+1 0] 2. 1200 31
- B [-2 +5] ÷ 1.870243098 - 1083 + 27/31 - 28
------------- ------------- --------------- ----
* [+3 -5] 1.069379699 116 + 04/31 3
s between perfect-4th and major-3rd:
8ve gen ~ratio cents 31-edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
F [+1 -1] 1.337329378 503 + 07/31 13
- E [-2 +4] ÷ 1.25056552 - 387 + 03/31 - 10
------------- ------------- --------------- ----
* [+3 -5] 1.069379699 116 + 04/31 3
* This always results in a change of letter-name.
In both historical chronology and the method of scale construction by generators, the chromatic-semitone first emerges in meantone as the interval between B and Bb:
C = n0
8ve gen ~ratio cents 31-edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
Bb [+2 -2] 1.788449866 1006 + 14/31 26
- B [-2 +5] ÷ 1.870243098 - 1083 + 27/31 - 28
------------- ------------- --------------- ----
b [+4 -7] 0.956265989 -77 + 13/31 29 = -2 mod 31
The "round-b" or "soft-b" was used to notate Bb, and eventually evolved into the "flat" symbol, defined as above. This signifies a flattening (lowering in pitch) by 2 degrees of 31-edo.
B-natural was notated as "square-b" or "hard-b". Gradually, as the scale was extended, this "square-b" evolved into both the "natural" and "sharp" symbols, and also resulted in the Eastern European practice of calling "B-flat" simply "b", with "B-natural" called "h".
C = n0
8ve gen ~ratio cents 31-edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
F# [-3 +6] 1.398490998 580 + 20/13 15
- F [+1 -1] ÷ 1.337329378 - 503 + 07/31 - 13
------------- ------------- --------------- ----
# [-4 +7] 1.045734148 +77 + 13/31 2
This is the interval of the "augmented unison" or "augmented prime", also known as the "chromatic semitone", and signifies a sharpening (raising in pitch) by 2 degrees of 31-edo.
Extending the system still further, to Eb -3 on the flat side and to D# +9 on the sharp side, we find a smaller interval, the "diminished 2nd":
C = n0
8ve gen ~ratio cents 31-edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
Eb [+2 -3] 1.195873274 309 + 21/31 8
- D# [-5 +9] ÷ 1.169430766 - 270 + 30/31 - 7
------------- ------------- --------------- ----
[+7 -12] 1.022611436 38 + 22/31 1
Extending the system still further, to Cb -7 on the flat side and to B# +12 on the sharp side, we find a new interval, the "augmented 7th" minus an "8ve", which, in 31-edo, is exactly the same size as the "diminished 2nd" discovered above:
C = n0
8ve gen ~ratio cents 31-edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
B# [ -6 +12] 1.95577707 1161 + 09/31 30
- Cb [ +5 -7] ÷ 1.912531979 - 1122 + 18/31 - 29
-------------- ------------- ---------------- ----
[-11 +19] 1.022611436 38 + 22/31 1
Finally, extending the system to Cbb -14 on the flat side and Ax +17 on the sharp side, we find the point where the system closes:
C = n0
8ve gen ~ratio cents 31-edo degrees
2(((18*gen)/31)+8ve) ((18*gen) mod 31)
Cbb [ +9 -14] 1.828889285 1045 + 05/31 27
- Ax [ -9 +17] ÷ 1.828889285 - 1045 + 05/31 - 27
--------------- ------------- ------------ ----
[+18 -31] 1 0 0
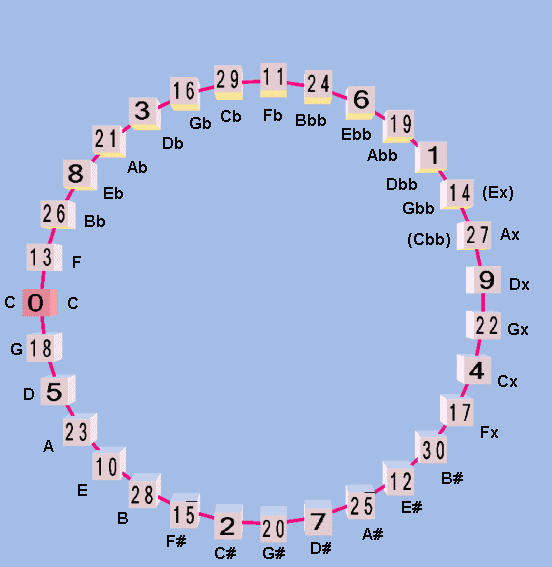
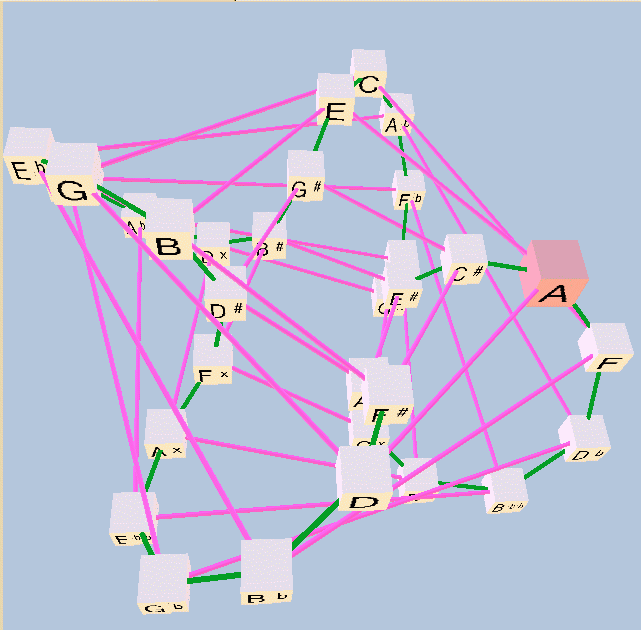
Below is a diagram of the 31-edo "circle-of-5ths" in this typical meantone usage, giving the 31-edo degree-numbers in the cubes and the letter-name notation alongside, showing the closure of the system between Gbb -13 = Ex +18 generators and Cbb -14 = Ax +17 generators:
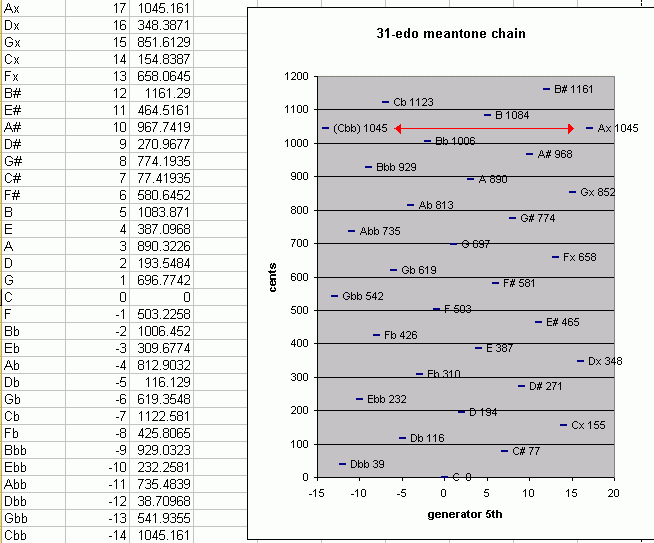
Below is a pitch-height graph of the complete 31-edo circle-of-5ths, shown as a meantone chain, centered on C. The red arrows connect the enharmonically equivalent notes at each end of the chain which are exactly the same pitch.
Below is the same circle-of-5ths-as-meantone-chain, shown on the regular 5-line staff notation, with a slur connecting the enharmonically equivalent notes.

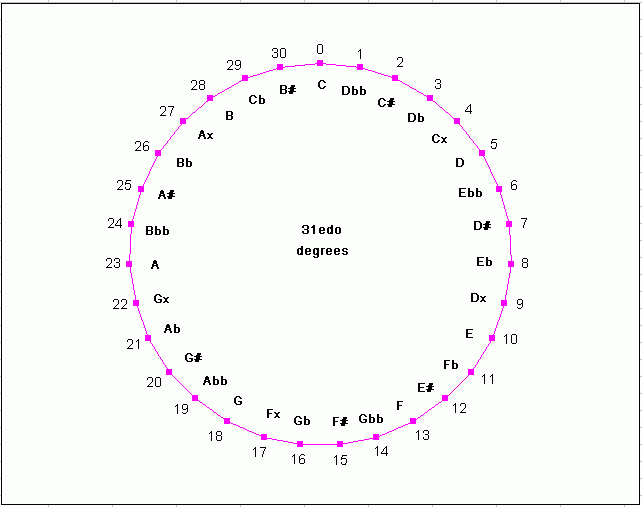
Below is a circular diagram of 31-edo with letter notation of its typical meantone usage, showing the degrees of 31-edo arranged according to pitch-height scalar order around the circle which represents the "8ve".
31-et circle of scale degrees
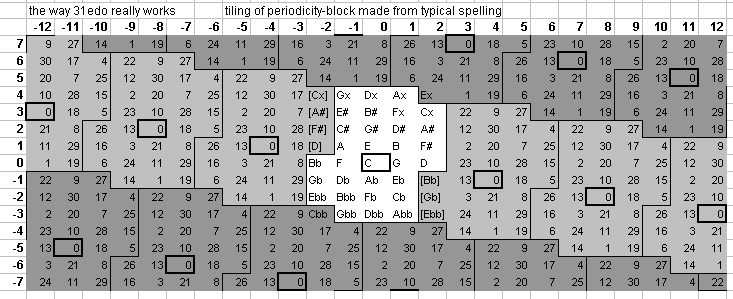
When used as a meantone, 31-edo is also intended to approximate ratios containing prime-factor 5 -- thus, a lattice of the just-intonation pitches being approximated becomes planar (2-dimensional) rather than simply linear (1-dimensional), i.e., another dimension is added to represent prime-factor 5. Below is a 2-dimensional 5-limit bingo-card lattice-diagram, showing a typical periodicity tiling of the 31-edo representations of 5-limit ratios, with a typical spelling in a chain from Gbb at -13 generators to Ax at +17 generators where C=n0 -- it would be difficult to find music from the "common-practice" (c. 1600-1900) repertoire which has notes falling outside this range.
Exponents of 3 run across the top row and exponents of 5 run in a column down the left side; C n0 is outlined in heavy black; syntonic-comma equivalents (which have the same spelling) are in a light shade of grey; enharmonically-equivalent pitches (which have a different spelling but are the same pitch as those in the central block) are in a darker shade of grey. Integers designate the degrees of 31-edo.
When used as a meantone, 31-edo provides not only a circle of "5ths" (i.e., tempered approximation of the 3:2 ratio), but also a circle of "major-3rds" (i.e., tempered approximation of the 5:4 ratio) -- in our example C-based lattice, this circle can be spelled C-E-G#-B#-Fbb-Abb-Cb-Eb-G-B-D#-Fx-Cbb-Ebb-Gb-Bb-D-F#-A#-Cx-Gbb-Bbb-Db-F-A-C#-E#-Gx-Dbb-Fb-Ab-C. The closed geometry which represents both of these circles simultaneously takes the form of a torus, with both circles twisted to form two interconnected spirals which outline the surface of the torus. Below is a graphic adapted from a Musica lattice (based on A instead of C), showing 31-edo as a torus, with the circle of 5ths as a closed tight spiral colored magenta, and the other closed spiral, representing major-3rds, wider and colored green.
31-edo 3,5-primespace toroidal lattice
(Be aware that 31-edo also belongs to other temperament families! ... namely, miracle, würschmidt, and orwell.)
Below is a table showing how some of the most common 11-limit just-intonation ratios, and some others up to the 41-limit, are mapped to 31-edo, using the closest-fit mappings:
====================================
edomap.py (c)2008-12-23 by Joe Monzo
====================================
Finds the EDO mappings for a set of ratios
=============== new run =====================
please enter edo: 31
31 -edo floating-point mappings:
prime edo-steps step-error edo-map
2 = 31.000000 +0.00 --> 31
3 = 49.133838 -0.13 --> 49
5 = 71.979771 +0.02 --> 72
7 = 87.028003 -0.03 --> 87
11 = 107.242380 -0.24 --> 107
13 = 114.713631 +0.29 --> 115
17 = 126.711348 +0.29 --> 127
19 = 131.685753 +0.31 --> 132
23 = 140.230421 -0.23 --> 140
29 = 150.597411 +0.40 --> 151
31 = 153.580086 +0.42 --> 154
37 = 161.493054 -0.49 --> 161
41 = 166.084112 -0.08 --> 166
integer (i.e., true) mappings, compared with cents-value of actual prime
map 2 --> 31 = 1200.000000 cents <-- 1200.000000 + 0.0 cents
map 3 --> 49 = 1896.774194 cents <-- 1901.955001 - 5.2 cents
map 5 --> 72 = 2787.096774 cents <-- 2786.313714 + 0.8 cents
map 7 --> 87 = 3367.741935 cents <-- 3368.825906 - 1.1 cents
map 11 --> 107 = 4141.935484 cents <-- 4151.317942 - 9.4 cents
map 13 --> 115 = 4451.612903 cents <-- 4440.527662 +11.1 cents
map 17 --> 127 = 4916.129032 cents <-- 4904.955410 +11.2 cents
map 19 --> 132 = 5109.677419 cents <-- 5097.513016 +12.2 cents
map 23 --> 140 = 5419.354839 cents <-- 5428.274347 - 8.9 cents
map 29 --> 151 = 5845.161290 cents <-- 5829.577194 +15.6 cents
map 31 --> 154 = 5961.290323 cents <-- 5945.035572 +16.3 cents
map 37 --> 161 = 6232.258065 cents <-- 6251.344039 -19.1 cents
map 41 --> 166 = 6425.806452 cents <-- 6429.062406 - 3.3 cents
--------------
examples:
ratio --> 31 -edo mapping:
ratio cents error edo cents name
2:1 = 1200.0 + 0.0 --> 31/31 = 1200.0 (octave)
31:16 = 1145.0 +16.3 --> 30/31 = 1161.3 (31st harmonic)
4096:2187 = 1086.3 +36.3 --> 29/31 = 1122.6 (pythagorean diminished-8ve)
243:128 = 1109.8 -25.9 --> 28/31 = 1083.9 (pythagorean major-7th)
15:8 = 1088.3 - 4.4 --> 28/31 = 1083.9 (just major-7th, 5*3)
13:7 = 1071.7 +12.2 --> 28/31 = 1083.9 (tridecimal superminor-7th)
11:6 = 1049.4 - 4.2 --> 27/31 = 1045.2 (undecimal submajor-7th)
20:11 = 1035.0 +10.2 --> 27/31 = 1045.2 (undecimal superminor-7th)
29:16 = 1029.6 +15.6 --> 27/31 = 1045.2 (29th harmonic)
9:5 = 1017.6 -11.1 --> 26/31 = 1006.5 (just minor-7th)
16:9 = 996.1 +10.4 --> 26/31 = 1006.5 (pythagorean minor-7th)
7:4 = 968.8 - 1.1 --> 25/31 = 967.7 (7th harmonic)
12:7 = 933.1 - 4.1 --> 24/31 = 929.0 (septimal supermajor-6th)
27:16 = 905.9 -15.5 --> 23/31 = 890.3 (pythagorean major-6th)
5:3 = 884.4 + 6.0 --> 23/31 = 890.3 (just major-6th)
18:11 = 852.6 - 1.0 --> 22/31 = 851.6 (undecimal neutral-6th)
13:8 = 840.5 +11.1 --> 22/31 = 851.6 (13th harmonic)
8:5 = 813.7 - 0.8 --> 21/31 = 812.9 (just minor-6th)
128:81 = 792.2 +20.7 --> 21/31 = 812.9 (pythagorean minor-6th)
6561:4096 = 815.6 -41.4 --> 20/31 = 774.2 (pythagorean augmented-5th)
11:7 = 782.5 - 8.3 --> 20/31 = 774.2 (undecimal augmented-5th)
25:16 = 772.6 + 1.6 --> 20/31 = 774.2 (just augmented-5th)
14:9 = 764.9 + 9.3 --> 20/31 = 774.2 (septimal subminor-9th)
3:2 = 702.0 - 5.2 --> 18/31 = 696.8 (perfect-5th)
16:11 = 648.7 + 9.4 --> 17/31 = 658.1 (11th subharmonic)
23:16 = 628.3 - 8.9 --> 16/31 = 619.4 (23rd harmonic)
10:7 = 617.5 + 1.9 --> 16/31 = 619.4 (septimal large-tritone)
1024:729 = 588.3 +31.1 --> 16/31 = 619.4 (pythagorean diminished-5th)
729:512 = 611.7 -31.1 --> 15/31 = 580.6 (pythagorean augmented-4th)
7:5 = 582.5 - 1.9 --> 15/31 = 580.6 (septimal small-tritone)
11:8 = 551.3 - 9.4 --> 14/31 = 541.9 (11th harmonic)
4:3 = 498.0 + 5.2 --> 13/31 = 503.2 (perfect-4th)
21:16 = 470.8 - 6.3 --> 12/31 = 464.5 (septimal-4th, 7*3)
9:7 = 435.1 - 9.3 --> 11/31 = 425.8 (septimal supermajor-3rd)
41:32 = 429.1 - 3.3 --> 11/31 = 425.8 (41st harmonic)
14:11 = 417.5 + 8.3 --> 11/31 = 425.8 (undecimal diminished-4th)
8192:6561 = 384.4 +41.4 --> 11/31 = 425.8 (pythagorean diminished-4th)
81:64 = 407.8 -20.7 --> 10/31 = 387.1 (pythagorean major-3rd)
5:4 = 386.3 + 0.8 --> 10/31 = 387.1 (just major-3rd)
11:9 = 347.4 + 1.0 --> 9/31 = 348.4 (undecimal neutral-3rd)
39:32 = 342.5 + 5.9 --> 9/31 = 348.4 (39th harmonic, 13*3)
6:5 = 315.6 - 6.0 --> 8/31 = 309.7 (just minor-3rd)
19:16 = 297.5 +12.2 --> 8/31 = 309.7 (19th harmonic)
32:27 = 294.1 +15.5 --> 8/31 = 309.7 (pythagorean minor-3rd)
13:11 = 289.2 +20.5 --> 8/31 = 309.7 (tridecimal diminished-3rd)
19683:16384 = 317.6 -46.6 --> 7/31 = 271.0 (pythagorean augmented-2nd)
7:6 = 266.9 + 4.1 --> 7/31 = 271.0 (septimal subminor-7th)
37:32 = 251.3 -19.1 --> 6/31 = 232.3 (37th harmonic)
8:7 = 231.2 + 1.1 --> 6/31 = 232.3 (septimal tone)
9:8 = 203.9 -10.4 --> 5/31 = 193.5 (pythagorean major-2nd/tone)
10:9 = 182.4 +11.1 --> 5/31 = 193.5 (just minor-tone)
11:10 = 165.0 -10.2 --> 4/31 = 154.8 (undecimal small-tone/submajor-2nd)
35:32 = 155.1 - 0.3 --> 4/31 = 154.8 (35th harmonic, 7*5)
12:11 = 150.6 + 4.2 --> 4/31 = 154.8 (undecimal large-semitone)
13:12 = 138.6 +16.3 --> 4/31 = 154.8 (tridecimal minor-2nd)
14:13 = 128.3 -12.2 --> 3/31 = 116.1 (tridecimal major-2nd)
15:14 = 119.4 - 3.3 --> 3/31 = 116.1 (septimal chromatic-semitone)
16:15 = 111.7 + 4.4 --> 3/31 = 116.1 (just diatonic-semitone)
17:16 = 105.0 +11.2 --> 3/31 = 116.1 (septendecimal semitone)
256:243 = 90.2 +25.9 --> 3/31 = 116.1 (pythagorean minor-2nd/limma)
2187:2048 = 113.7 -36.3 --> 2/31 = 77.4 (pythagorean augmented-prime/apotome)
25:24 = 70.7 + 6.7 --> 2/31 = 77.4 (just chromatic-semitone)
33:32 = 53.3 -14.6 --> 1/31 = 38.7 (33rd harmonic, 11*3)
1:1 = 0.0 + 0.0 --> 0/31 = 0.0 (prime)
some commas:
3-limit:
531441:524288 = 23.5 -62.2 --> -1/31 = -38.7 (pythagorean-comma)
5-limit:
648:625 = 62.6 -23.9 --> 1/31 = 38.7 (major-diesis)
250:243 = 49.2 +28.3 --> 2/31 = 77.4 (maximal-diesis)
128:125 = 41.1 - 2.3 --> 1/31 = 38.7 (enharmonic-diesis)
34171875:33554432 = 31.6 -31.6 --> 0/31 = 0.0 (ampersand-comma)
3125:3072 = 29.6 + 9.1 --> 1/31 = 38.7 (magic-comma)
81:80 = 21.5 -21.5 --> 0/31 = 0.0 (syntonic-comma)
2048:2025 = 19.6 +19.2 --> 1/31 = 38.7 (diaschisma)
2109375:2097152 = 10.1 -10.1 --> 0/31 = 0.0 (semicomma)
15625:15552 = 8.1 +30.6 --> 1/31 = 38.7 (kleisma)
32805:32768 = 2.0 -40.7 --> -1/31 = -38.7 (skhisma)
7-limit:
36:35 = 48.8 -10.1 --> 1/31 = 38.7 (septimal-diesis)
49:48 = 35.7 + 3.0 --> 1/31 = 38.7 (septimal-comma-3 - 7/6 : 8/7)
50:49 = 35.0 + 3.7 --> 1/31 = 38.7 (septimal-comma-2)
64:63 = 27.3 +11.4 --> 1/31 = 38.7 (septimal-comma)
225:224 = 7.7 - 7.7 --> 0/31 = 0.0 (septimal-kleisma)
11-limit:
22:21 = 80.5 - 3.1 --> 2/31 = 77.4 ()
33:32 = 53.3 -14.6 --> 1/31 = 38.7 (undecimal-diesis)
45:44 = 38.9 - 0.2 --> 1/31 = 38.7 ()
55:54 = 31.8 + 6.9 --> 1/31 = 38.7 ()
56:55 = 31.2 + 7.5 --> 1/31 = 38.7 ()
121:120 = 14.4 -14.4 --> 0/31 = 0.0 (11/10 : 12/11 comma)
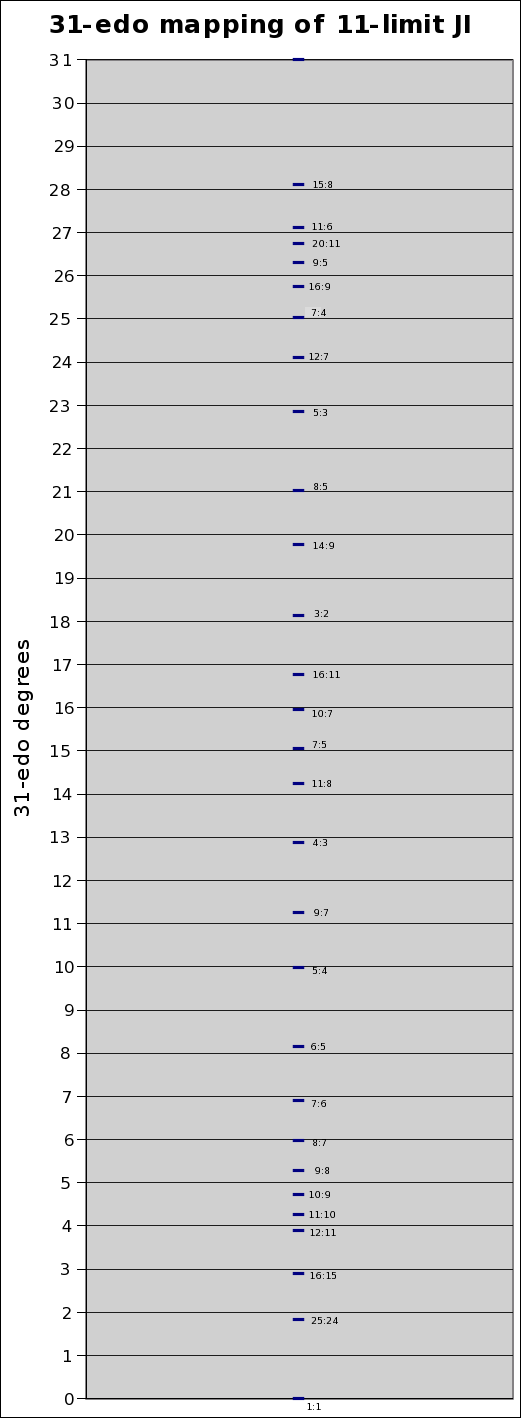
Below is a graph showing the degrees of 31-edo as the Y-axis grid, with the pitch of the 11-limit JI ratios plotted against it:
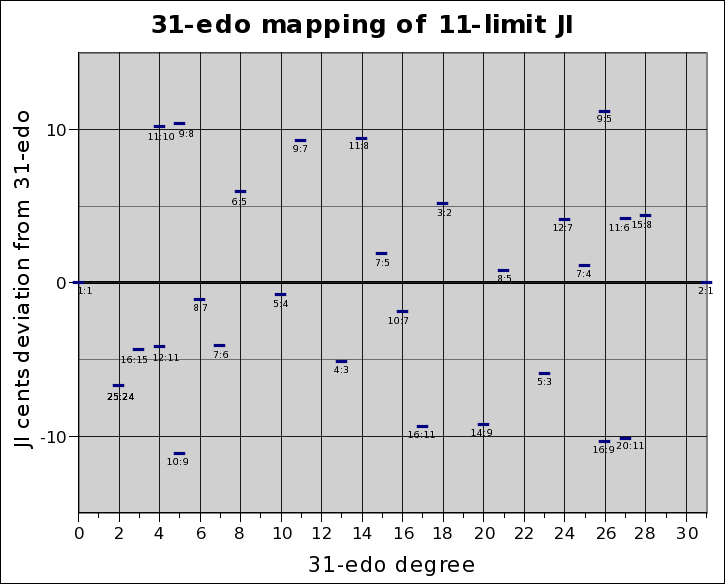
Below is a graph showing the degrees of 31-edo along the X-axis, with the Y-value of zero representing the pitch of the 31-edo degrees, and the deviation of the JI ratios from the 31-edo degrees plotted against that:
| 31=0 | 2:1 = 1:1 |
| 30 | 43:22 , 45:23 , 88:45 , 133:68 , 221:113 , 575:294 |
| 29 | 21:11 , 44:23 , 153:80 |
| 28 | 15:8 , 43:23 , 101:54 , 245:131 |
| 27 | 11:6 , 64:35 , 139:76 , 342:187 , 481:263 |
| 26 | 9:5 , 25:14 , 34:19 , 59:33 , 93:52 |
| 25 | 7:4 , 397:227 |
| 24 | 12:7 , 53:31 , 65:38, 118:69 , 183:107 , 301:176 |
| 23 | 5:3 , 97:58 |
| 22 | 18:11 , 157:96 |
| 21 | 8:5 , 435:272 , 443:277 |
| 20 | 11:7 , 25:16 , 61:39 , 208:133 |
| 19 | 26:17 |
| 18 | 3:2 , 166:111 |
| 17 | 19:13 , 117:80 , 253:173 , 370:253 |
| 16 | 10:7 , 123:86 , 133:93 |
| 15 | 7:5 , 186:133 |
| 14 | 11:8 , 15:11 , 26:19 , 67:49 , 93:68 , 253:185 |
| 13 | 4:3 , 111:83 |
| 12 | 17:13 |
| 11 | 9:7 , 23:18 , 55:43 , 78:61 , 133:104 |
| 10 | 5:4 |
| 9 | 11:9 , 192:157 |
| 8 | 6:5 , 55:46 , 116:97 |
| 7 | 7:6 , 69:59 , 283:242 , 352:301 |
| 6 | 8:7 , 223:195 , 231:202 |
| 5 | 9:8 , 19:17 , 85:76 , 104:93 |
| 4 | 11:10 , 12:11 , 35:32 , 152:139 , 187:171 |
| 3 | 15:14 , 31:29 , 77:72 , 185:173 , 262:245 |
| 2 | 22:21 , 23:22 , 160:153 |
| 1 | 42:41 , 43:42 , 44:43 , 45:44 , 181:177 |
| 0 | 1:1 |
| progressing to the right = greater accuracy of approximation and greater complexity | |
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by selecting the highest level of financial support that you can afford. Thank you.
