tone-space
A tone-space is a real-space in which the basis-vectors have a certain specific meaning, which is an exponent of some base. It is similar to an integral vector space, i.e., all coordinate values are integers. It is one of the file types supported by Tonalsoft™ Tonescape™ microtonal music composition software; this page will describe tone-spaces as implemented by Tonescape™, where the term is written as "Tonespace".
The origin of the tone-space represents the frequency-multiplier 1, which represents some reference pitch (for example, the standard international reference pitch A-440). The number of dimensions in the tone-space corresponds to the number of axes which are used to define the space, and each axis of the space represents a generator of the tuning. The bases (axes) are typically numbers from the prime series -- in unaltered form, these produce just intonation or other rational intonations; if the pitch values are altered slightly from the true prime numbers, they produce a temperament. A subspace of tone-space is prime-space.
Tonescape employs methods derived from Fokker's music theory, in which certain pairs of notes called "unison-vectors" are considered to be equivalent, each unison-vector closing off one dimension of the space. In a 2-dimensional space, for example, two unison-vectors will form a parallelogram which encloses a subset of pitches from the tone-space, and the pitches encompossed within all tilings of that parallelogram are considered to be equal to the pitches within it. This both provides a method for selection of a closed set of just intonation pitches, and suggests a cardinality for an equal temperament.
A detailed exploration of creating a Tonescape tone-space can be found in our Tonescape Tutorial: How to use "File | New | Tonespace".
When creating a Tonespace in Tonescape, the first step is to choose the generators which form the axes of the Lattice diagram. In this example, we will create a Tonespace using prime numbers as our generators, and prime-factor 2 will be our identity interval and will not be shown on the Lattice; thus, prime-factors 3 and 5 will form the axes of our 2-dimensional space:
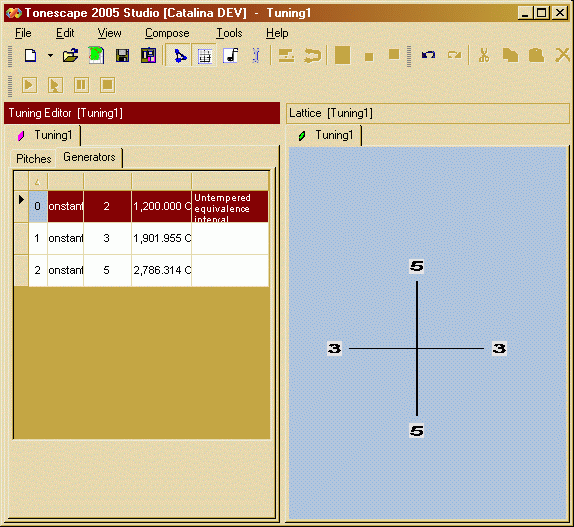
The theoretically infinite lattice is assumed for a tonespace, and thus Tonescape does not put any Lattice Points into the diagram until at least one unison-vector is selected. For purposes of illustration, here we have created an Euler-genus described as 3-3...4 * 5-3...3; Tonescape allows many different kinds of notation on the Lattice -- the first illustration shows it with Prime-Ratio notation, which expresses directly the exponents in the Euler-genus:
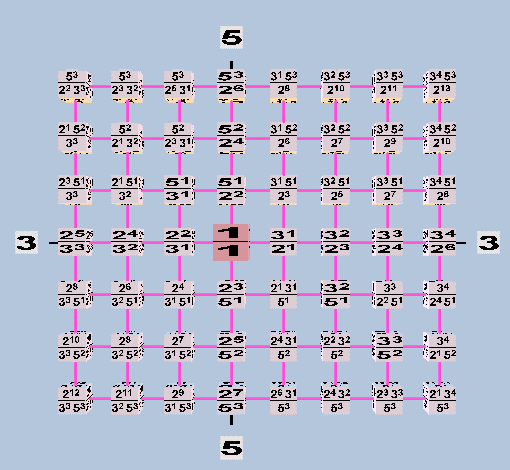
The next illustration shows the same Euler-genus, using regular Ratio notation:

The next illustration shows the same Euler-genus, using Logarithmic Cents notation:
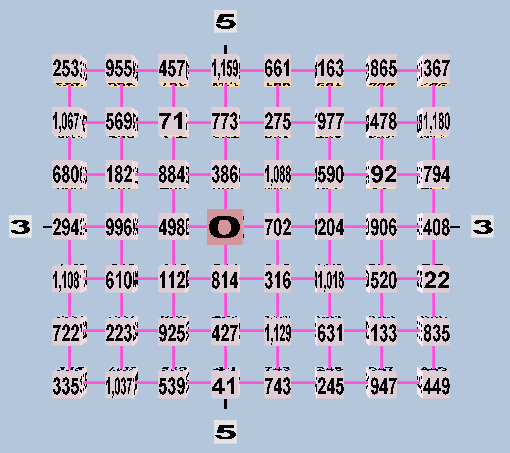
And finally, the next illustration shows the same Euler-genus, using standard pythagorean/meantone letter-name notation with sharps and flats:

Next, we will select a unison-vector, so that Tonescape will form a band of pitches, and filter out all notes which are a unison-vector (or a multiple of the unison-vector) away from the notes within the band. Here, we have selected the syntonic-comma with ratio 81/80 and 2,3,5-monzo |-4 4, -1 > as our unison-vector -- this creates the open-ended tuning known as 1/4-comma meantone (or with slight adjustments, any open-ended member of the meantone family); because the vector of the syntonic-comma appears as mainly left-to-right on the Lattice, the band of pitches is theoretically open-ended at the top and bottom, but is closed off on the left and right sides:
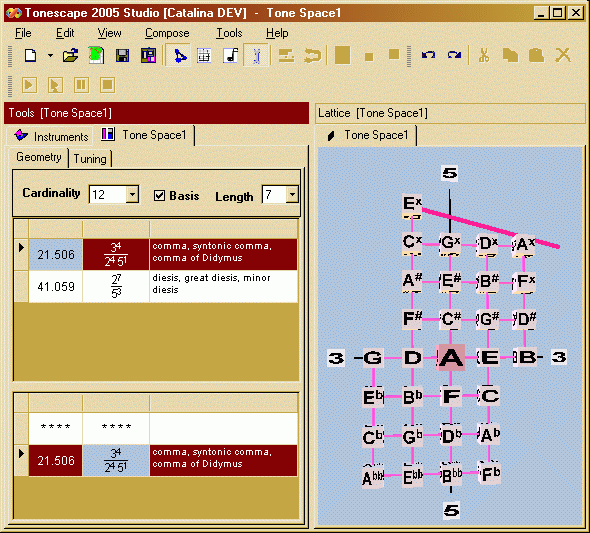
When Tonescape's Lattice geometry is set to "closed curved", the Lattice is twisted so that the left and right sides of the band of pitches meet, and form a 4-strand helix:
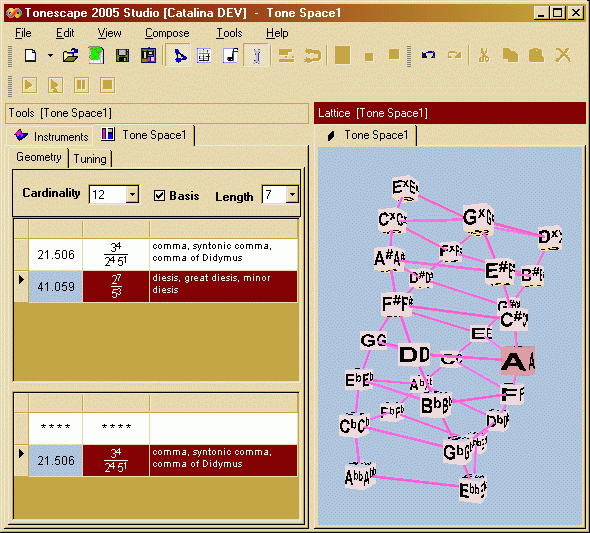
Because our space is 2-dimensional, if we select 2 unison-vectors, we will close off both dimensions and create a closed tuning. For our example, we will create a Tonespace which is appropriate for 12-edo. Tonescape tells us that the TM-reduced Basis unison-vectors for 12-edo are the syntonic-comma, and the diesis with ratio 128/125 and 2,3,5-monzo |7 0, -3 > :
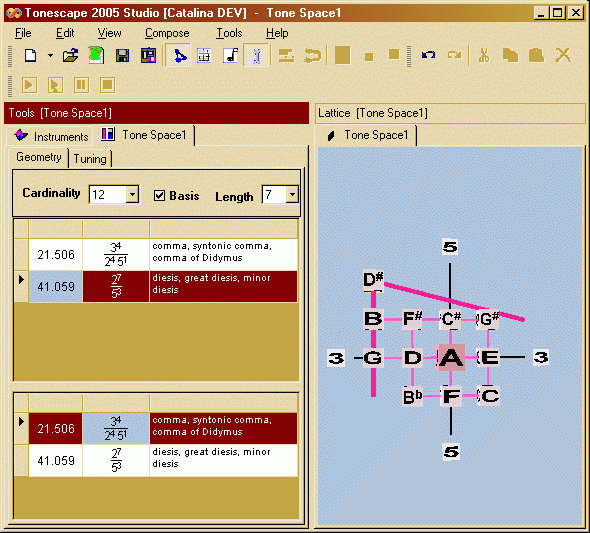
When Tonescape's Lattice geometry is set to "closed curved" for this tuning, the Lattice is twisted twice, into a torus:
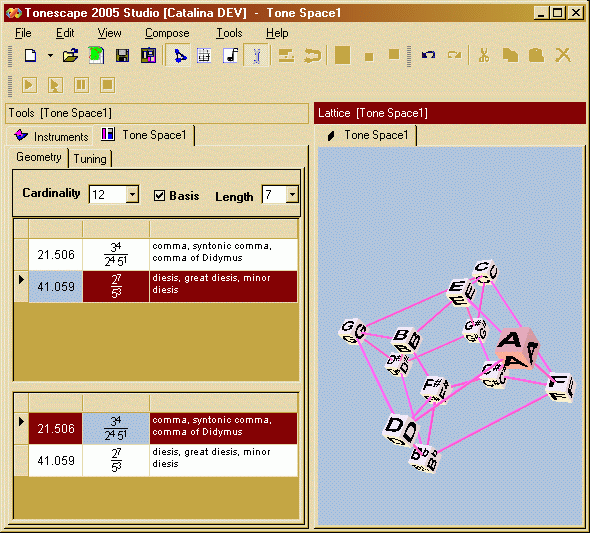
The periodicity bands and blocks thus created by Tonescape may be used in just intonation, or may be further edited so that they create temperaments.
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
