© 2002 by Joe Monzo
In this webpage I propose to explore the method by which it might be possible for a Sumerian to calculate string-lengths which divide a string into a tuning which closely approximates 12-tone equal-temperament, using the same method as explained on my Speculations on Sumerian Tuning page, but to an accuracy of only 2 sexagesimal places.
The Sumerians used the sexagesimal (= base-60) place-notation numbering system in their written calculations and math tables. I will therefore use this system to show how a Sumerian could obtain successively closer approximations to a desired irrational value.
Since our perception of pitch is related logarithmically to the mathematics of rational division and multiplication, what we perceive as equal division of frequency, is mathematically calculated by taking roots of frequencies or string-lengths.
Another preliminary fact that must be noted is that measurement of string-lengths is inversely proportional to the perception of the resulting frequencies. Thus, the mid-point of a length of string would be 1/2 the length of the total string, and the frequency would be double that of the total string, thus giving a ratio of 2:1.
We will assume that our hypothetical Sumerian is measuring the frequencies on a monochord string. For convenience, the length of the entire string will be 60 units, which we'll also label as 0 cents. The "8ve" (1200 cents) occurs at the midpoint of 30 units.
As I demonstrate the basic calculations to determine the so-called "Pythagorean" scale, I will also review basic sexagesimal (= "base-60") math.
For the purpose of aiding in understanding for a modern
musically-literate reader, let's call our string by the
modern letter-name "F". (All ancient people used very different names.)
Of course, the "8ve" will also be "F". I'll supply
crude ASCII diagrams which don't show the lengths
at the proper proportions, but at least give a general
idea of the string divisions, which are given in both
base-60 and regular decimal fractions.
∞ + (bridge)
|
|
|
|
|
|
|
|
30 + F 1/2
|
|
|
|
|
|
|
|
|
|
|
60 + F 1/1
To descend a
"perfect 4th"
(ratio 4:3, ~498 cents)
from the "8ve", we have
to multiply 1/2 by 4/3, or 30/60 by 80/60. This
80/60 = 1 + 20/60, so is written sexagesimally as 1;20.
(1/2) * (4/3) = 2/3 = 40/60. So the problem and its answer
is written sexagesimally as:
1;20
* 30
-----
40
In sexagesimal math, multiplying by 30 is the same as
dividing in half (just as multiplying by .5 is the same
for us in decimal). So the above can be translated into:
(60 + 20)
* .5
----------
(30 + 10) = 40
Thus, the "C" a "perfect 4th" below our "8ve" of "F",
and thus simultaneously a
"perfect 5th"
(ratio 3:2, ~702 cents) above
the lower "F", occurs at 40 units from the bridge.
∞ + (bridge)
|
|
|
|
|
|
|
|
30 + F 1/2
|
|
|
|
40 + C 2/3
|
|
|
|
|
|
60 + F 1/1
We repeat this procedure to find the "perfect 4th" below "C",
(ratio 9:8, ~204 cents) which would be
13 carry row
1;20
* 40
------
53,20 answer
In sexagesimal math, whenever answers in any "cell"
exceed 60, one divides by 60, writes
down the remainder in the "cell", and carries the quotient over into
the next column to the left (noted here as "carry rows").
Here, 20 * 40 = 800. Since 60 * 13 = 780, which is the closest
mupltiple of 60 to 800, and 800 - 780 = 20, we write down "20"
and carry 13. 40 * 1 = 40, then we add the 13 + 40 to get 53.
So the note "G" is 53,20 (which we call 53 & 1/3) units
from the bridge.
∞ + (bridge)
|
|
|
|
|
|
|
|
30 + F 1/2
|
|
|
|
40 + C 2/3
|
|
|
|
53,20 + G 8/9
|
60 + F 1/1
Now, to find the "D" a "perfect 5th" *above* "G", we
*divide* the measurement for "G" by the ratio 3:2, which
is the same as multiplying by 2/3, which in sexagesimal
is again a multiplication by 40:
35 13 carry row
53 20
* 40
---------
35 33 20 answer
Again, 20 * 40 = 800, 60 * 13 = 780, 800 - 780 = 20, so write down remainder of 20, and carry 13. 53 * 40 = 2120, add 13 = 2133. Since 60 * 35 = 2100, and 2133 - 2100 = 33, write down remainder of 33 and carry 35 into next column. There is no multiplicand for this column, so 35 is carried down by itself into the answer.
We round off to two sexagesimal places,
thus, "D" occurs at 35,33 units from the bridge.
The unrounded, correct string-length is 16/27,
and this rounded value is 237/400.
∞ + (bridge)
|
|
|
|
|
|
|
|
30 + F 1/2
|
|
35,33 + D 237/400 (theoretically 16/27)
|
40 + C 2/3
|
|
|
|
53,20 + G 8/9
|
60 + F 1/1
This procedure can be easily carried out by hand, until
one reaches the thirteenth pitch (our "E#") and finds that
it is very close to the "8ve":
-------------- string-length ----------------
theoretical ------------ actual -------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
|
.
.
.
+ E# 262144/531441 29,35 71/144 0.493055556 1224.213458
+ F 1/2 30 1/2 0.5 1200
+ E 128/243 31,36 79/150 0.526666667 1110.045531
+ D# 32768/59049 33,17 1997/3600 0.554722222 1020.195089
+ D 16/27 35,33 237/400 0.5925 906.1355291
+ C# 4096/6561 37,27 749/1200 0.624166667 815.9961384
+ C 2/3 40 2/3 0.666666667 701.9550009
+ B 512/729 42,8 158/225 0.702222222 612.0005316
+ A# 131072/177147 44,23 2663/3600 0.739722222 521.9333736
+ A 64/81 47,24 79/100 0.79 408.0905299
+ G# 16384/19683 49,56 749/900 0.832222222 317.9511393
+ G 8/9 53,20 8/9 0.888888889 203.9100017
+ F# 2048/2187 56,11 3371/3600 0.936388889 113.7843351
+ F 1/1 60 1/1 1 0
Thus it would be immediately apparent as soon as one arrives at 29,35 for "E#" that the ratio for "E#" would be slightly less than 30/60, and this would constitute numeric proof that the "8ve" is not equal to 6 "whole-tones" (of ratio 9:8). This ratio of 531441/524288 (its approximation in this 2-place base-60 calculation is 72/71) is known to us today as the "Pythagorean comma", but obviously the recognition of it must have occurred long before Pythagoras's lifetime.
By the way, this 2-sexagesimal-place approximation to Pythagorean tuning has an average error of only ~1/3-cent and a maximum error of ~3/4-cent.
It might be useful at this point to check some of these numbers, to show explicitly the conversion between sexagesimal and decimal math.
We may choose as our example the ratio of the Pythagorean "major 3rd", which we know as ratio 81:64. What I will show here is the method for converting from our decimal notation into sexagesimal notation, or converting the denominator from units of 81 to units of 60.
81 is 60 + 21, or sexagesimal 1;21. The reciprocal of 1;21 is 44,26,40, well attested in many Babylonian math texts.
64 is 60 + 4, written 1;4.
2 1 2 multiplication carry row
44,26,40
* 1; 4
===========
1 1 addition carry row
-----------
2 57 46 40 results of multiplying 44,26,40 by 4
44 26 40 - results of multiplying 44,26,40 by 1, shifted one place
-----------
47,24,26,40 final answer
This result is fairly close to 47,30, which is the exact midpoint between 47 and 48 units.
The Babylonian tablets attest that the Sumerians had worked out a sophisticated _thetic_ system of modal classification. It would be easy to understand this system in the _dynamic_ sense if the discrepancy at the end of the cycle (the "Pythagorean comma") was divided up and distributed among all the other intervals, which would result in 12-tone equal-temperament.
The Sumerians were capable of finding good approximations for both square- and cube-roots, so in determining a measurement for a tempered scale, the starting point would be to find a string-length for the tempered "major 3rd", since that would be the cube-root of 1/2, or to a Sumerian, the cube-root of 30.
So we begin by knowing that three successive Pythagorean "major 3rds" exceed an "8ve", but that three successive JI (i.e., 5-limit) "major 3rds" produce an interval which is smaller than an "8ve". Thus, we are looking for a tempered "major 3rd", and that tempered version lies between the two familiar rational intervals.
So we'll restate the above paragraph in sexagesimal mathematical terms, and also relate it to our familiar measurement of cents.
The JI "3rd" is the 5:4 ratio (~386.3 cents), which is
4/5 or 48/60 of the string-length as measured
from the bridge. The Pythagorean "3rd" is the 81:64 ratio
(~407.82 cents), which is almost midway between 47/60 and 48/60.
We want to find the fraction of 60 which gives the 400-cent "3rd".
As before, I will illustrate by creating a schematic diagram of the
string-lengths, not exactly to scale.
-------------- string-length ----------------
theoretical ------------ actual -------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ A 64/81 47,24 79/100 0.79 408.0905299
|
|
|
+ A 4/5 48 4/5 0.8 386.3137139
So first we find the cube of 4/5, or in modern notation,
(4/5)^3.
48 JI "major-3rd"
* 48
-------
38,24
38,24
* 48
--------
30,43,12
Thus, the measurement of (4/5)^3 is slightly farther from the bridge than the string's midpoint of 30, making the interval composed of three 5:4's somewhat smaller than the "8ve". In our modern rational notation we call it 125:64, ~1158.94 cents.
In our calculations above, we have already found that (64/81)^3 is measured at ~29,35 units from the bridge, making that interval somewhat larger than the "8ve". In our notation it's 71:144, ~1224.213458 cents (theoretically 531441:262144, ~1223.46 cents.)
So we begin by taking the mean value of these two "major 3rds".
Start by adding together the two terms:
1
47 24 Pythagorean "major-3rd" 81:64
+ 48 JI "major-3rd" 5:4
---------
1 35 24
Then divide each of these numbers by 2:
0.5 17.5 12
We need to remove the decimal components, so we remove
.5 from 17 and add 30 to the 12 in the column to the right of it:
0.5 17 42
Then we also remove .5 from the first column and add 30
to the 17 in the column next to the right of it:
47 42
So our first answer for the tempered "major 3rd" is 47,42 units from the bridge.
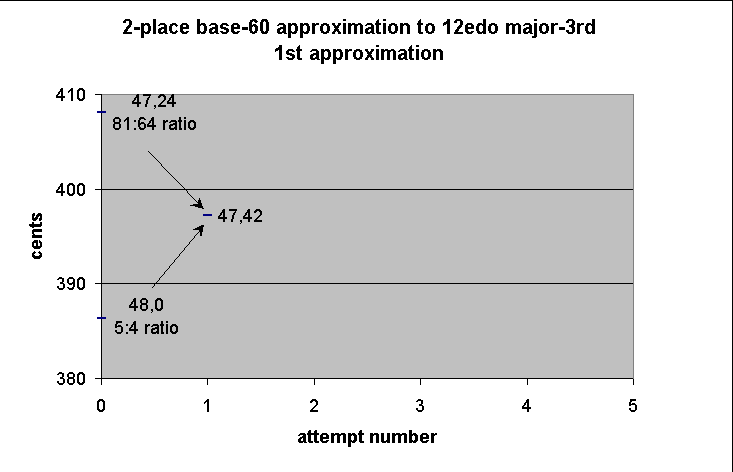
-------------- string-length ----------------
theoretical ------------ actual -------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ A 64/81 47,24 79/100 0.79 408.0905299
|
|
+ A 47,42 159/200 0.795 397.1678814
+ A 4/5 48 4/5 0.8 386.3137139
Next we check on the accuracy of this result by cubing it.
I will assume from this point on that the reader is capable
of performing the intermediate steps in the arithmetic.
In practice, it is unnecessary to carry the accuracy out
to more than three places, because differences beyond that
would be inaudible -- within the reference "8ve" between
30 and 60 parts (i.e., from 1/2 to the whole string),
the second sexagesimal place represents a maximum variation
of ~57 cents, the third place of only ~1 cent.
47 42
* 47 42
---------
~37 55
* 47 42
---------
~30 9
(in sexagesimal, the exact cube of 47,42 is 30,8,51,19,58,48)
So we see that stacking three of these tempered "major 3rds"
results in an interval measured at ~30,9 units from the bridge,
or ~1191.365398 cents. This is considerably closer than either of
the untempered "3rds", but can still
be improved. So we find another mean, this time between the
result we just calculated, which is still a bit too small, and the
Pythagorean "major 3rd", which is too large.
1
47 24 Pythagorean "major-3rd" 81:64
+ 47 42 1st approximation of 12edo "major-3rd"
---------
1 35 6
/ 2
---------
47 33
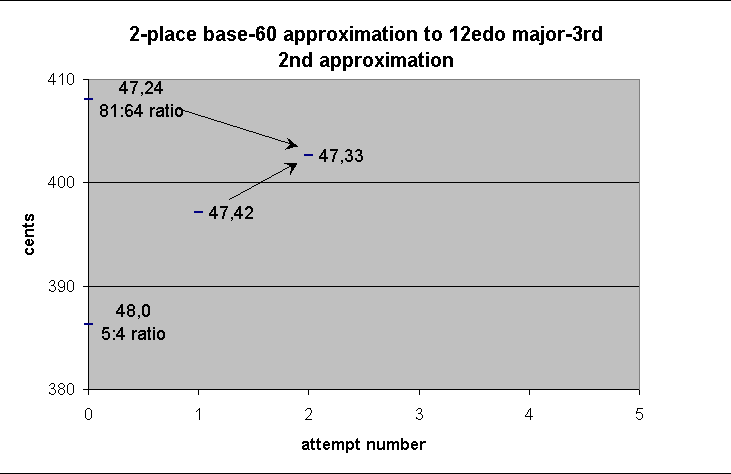
-------------- string-length ----------------
theoretical ------------ actual -------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ A 64/81 47,24 79/100 0.79 408.0905299
+ A 47,33 317/400 0.7925 402.6205916
|
+ A 47,42 159/200 0.795 397.1678814
+ A 4/5 48 4/5 0.8 386.3137139
Now we check the accuracy of this subdivision by cubing it:
47 33
* 47 33
--------
~37 41
* 47 33
--------
~29 52
This result, measured 29,52 units from the bridge, is ~1207.711523 cents. Now this is a bit too large, but still the closest result so far.
Since the last two values are both about equally far
away from our target, we'll take one more mean and that
should give a sufficiently accurate result.
So now we find the mean between the two
tempered "3rds" which we've calculated:
47 42 1st approximation of 12edo "major-3rd"
+ 47 33 2nd approximation of 12edo "major-3rd"
----------
1 35 15
/ 2
----------
47 38
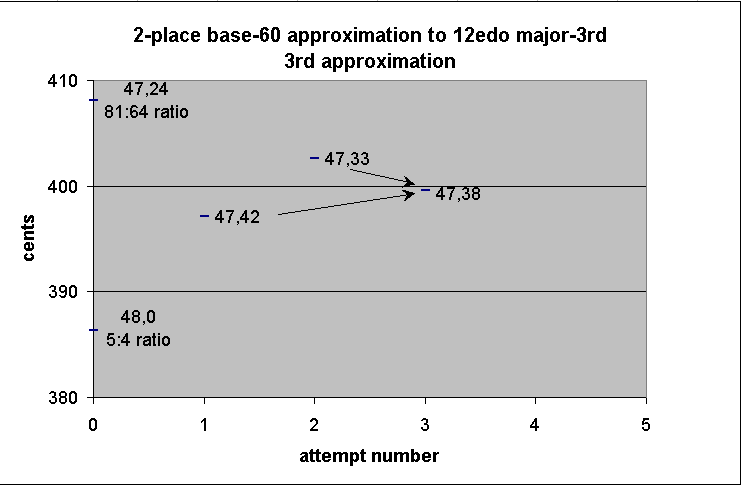
-------------- string-length ----------------
theoretical ------------ actual -------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ A 64/81 47,24 79/100 0.79 408.0905299
+ A 47,33 317/400 0.7925 402.6205916
+ A 47,38 1429/1800 0.7938889 399.5891881
+ A 47,42 159/200 0.795 397.1678814
+ A 4/5 48 4/5 0.8 386.3137139
Cube this to check accuracy:
47 38
* 47 38
--------
~37 49
* 47 38
--------
~30 1
Here we have finally found an interval which is audibly indistinguishable from the "8ve". It would be measured at 30,1 units from the bridge, which for all practical purposes is the same as 30. If it could be produced accurately, it would measure ~1199.03847 cents.
So we will set down the value for our tempered "major 3rd" as 47,38 units. This is ~399.5891881 cents.
Our next task is to determine the value of the tempered "whole-tone", which we obtain by finding successively closer approximations to the square-root of our tempered "major 3rd".
We do this by again taking the mean of two values which
we already know to be close to our target. In this case,
our starting ratios will be the Pythagorean "whole-tone"
of ratio 9:8 (~203.91 cents, 53,20 units from the bridge)
and the other "whole-tone" which commonly occurs in 5-limit
JI, of ratio 10:9 (~182.4 cents, 54 units from the bridge).
-------------- string-length ----------------
theoretical ------------ actual -------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ G 8/9 53,20 8/9 0.888888889 203.9100017
|
|
|
|
+ G 9/10 54 9/10 0.9 182.4037121
53 20 large Pythagorean "whole-tone" 9:8
+ 54 small JI "whole-tone" 10:9
--------
1 47 20
/ 2
--------
53 40
In this case the mean is actually very easy to compute mentally: 54 is the same as 53,60, and so the difference between the two terms is 0,40, whose mean is 20. Add 0,20 to 53,20 to get 53,40.
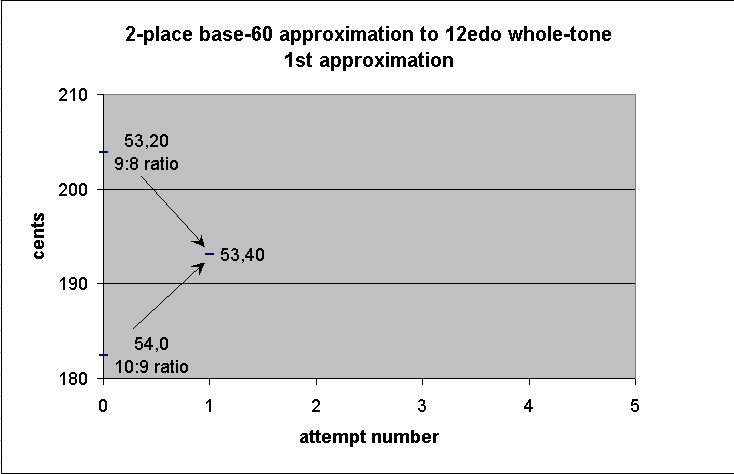
-------------- string-length ----------------
theoretical ------------ actual -------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ G 8/9 53,20 8/9 0.888888889 203.9100017
|
|
|
+ G 53,40 161/180 0.894444444 193.1234619
+ G 9/10 54 9/10 0.9 182.4037121
Now square 53,40 to see how closely it matches our tempered
"major 3rd":
53 40
* 53 40
------------
48 0 6 40
This is not too close to our goal, but note in passing that it *is* almost exactly the same as the JI "major 3rd" of ratio 5:4, which is exactly 48 units from the bridge. Thus, 53,40 units gives an extremely accurate "meantone", ~193.123 cents. Compare with the ~193.157 cents for the true meantone of (5/4)^(1/2). (Could meantone thus also be 5000 years old? To my mind, it is entirely possible that the Sumerians may have grappled with the calculation of this tuning also ... perhaps i'll write another webpage about that someday.)
So we continue by finding another mean, this time between the Pythagorean "major 3rd" and the "meantone" just calculated. This one is a trivial mental calculation, as one can easily see that the mean between 53,20 and 53,40 is 53,30.
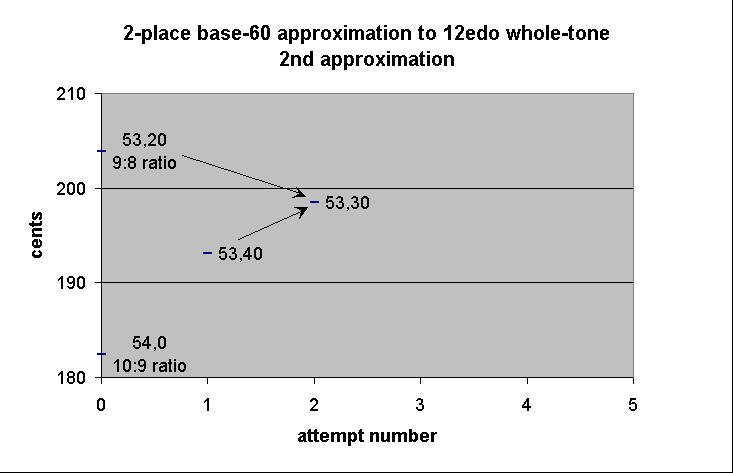
-------------- string-length ----------------
theoretical ------------ actual -------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ G 8/9 53,20 8/9 0.888888889 203.9100017
|
|
+ G 53,30 107/120 0.891666667 198.508331 2nd approximation
+ G 53,40 161/180 0.894444444 193.1234619 1st approximation
+ G 9/10 54 9/10 0.9 182.4037121
Square it to check the accuracy:
53 30
* 53 30
--------
47 42 15
This measurement, ~397.017 cents, is indeed quite close to our tempered "major 3rd" of 47,38 units.
Let us try to improve on this by taking the mean of this new "whole-tone" and the Pythagorean "whole-tone". Again the calculation is trivial: the mean of 53,20 and 53,30 is 53,25.
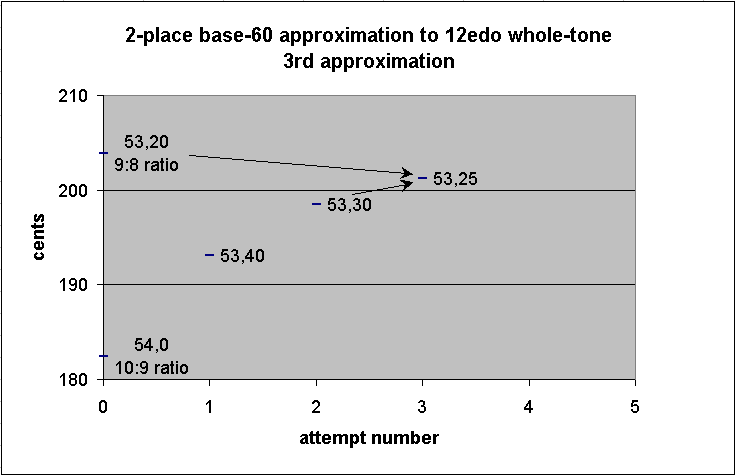
-------------- string-length ----------------
theoretical ------------ actual -------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ G 8/9 53,20 8/9 0.888888889 203.9100017
+ G 53,25 641/720 0.890277778 201.2070597 3rd approximation
|
+ G 53,30 107/120 0.891666667 198.508331 2nd approximation
+ G 53,40 161/180 0.894444444 193.1234619 1st approximation
+ G 9/10 54 9/10 0.9 182.4037121
Square it to check the accuracy:
53 25
* 53 25
----------
~47 33 20
This is ~402.42 cents.
Let us do one more calculation to get closer. This time we will take the mean between the last two calculated "whole-tones". The exact midpoint of 53,25 and 53,30 is 53,27,30, which my be rounded either up or down to two places; we may choose 53,28.
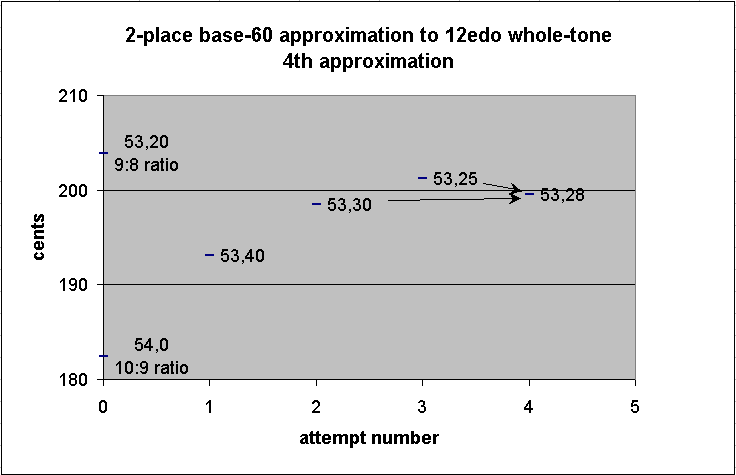
-------------- string-length ----------------
theoretical ------------ actual -------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ G 8/9 53,20 8/9 0.888888889 203.9100017
+ G 53,25 641/720 0.890277778 201.2070597 3rd approximation
+ G 53,28 401/450 0.891111111 199.5873177 4th approximation
+ G 53,30 107/120 0.891666667 198.508331 2nd approximation
+ G 53,40 161/180 0.894444444 193.1234619 1st approximation
+ G 9/10 54 9/10 0.9 182.4037121
Square it to check accuracy:
53 28
* 53 28
-------
~47 39
That's almost exactly our tempered "major 3rd". Thus, we can set down our tempered "whole-tone" at 53,28 units, ~199.587 cents.
The final remaining task is to find the tempered "semitone" by taking the square-root of this tempered "whole-tone".
Here we can begin with the two familiar Pythagorean semitones,
the _limma_ of ratio 256:243 (~90.225 cents) and the _apotome_
of ratio 2187:2048 (~113.7 cents). The measurement of the
former will be ~56,57 units from the bridge, and of the
latter, ~56,11 units.
--------------- string-length -----------------
theoretical ------------- actual --------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ F#/Gb 2048/2187 56,11 3371/3600 0.936388889 113.7843351 apotome
|
|
|
|
|
+ F#/Gb 243/256 56,57 1139/1200 0.949166667 90.31999055 limma
First we find the mean:
56 57 limma
+ 56 11 apotome
---------
1 53 8
/ 2
---------
56 34 1st approximation of 12edo semitone
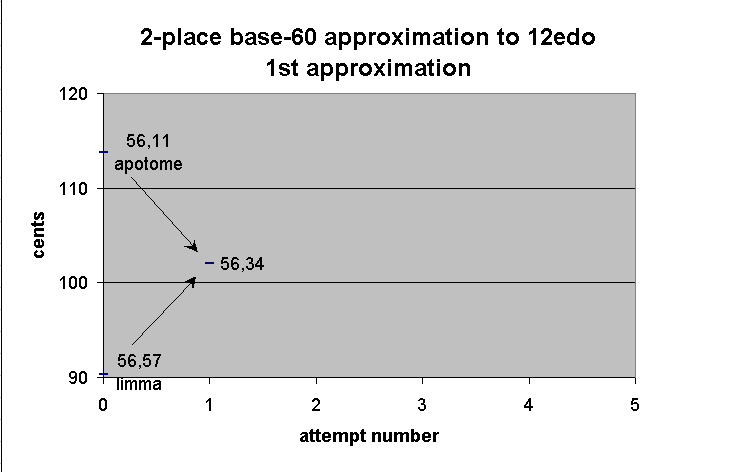
--------------- string-length -----------------
theoretical ------------- actual --------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ F#/Gb 2048/2187 56,11 3371/3600 0.936388889 113.7843351 apotome
+ F#/Gb 56,34 1697/1800 0.942777778 102.01241 1st approx. of 12edo semitone
|
|
|
|
+ F#/Gb 243/256 56,57 1139/1200 0.949166667 90.31999055 limma
Then we square it to see how close the result comes to
our tempered "whole-tone" of 53,28 units:
56 34
* 56 34
-------
~53 20
This is good, but we can do better.
Since our first calculated "semitone" is a bit larger
than the target, we take the mean of this and the _limma_:
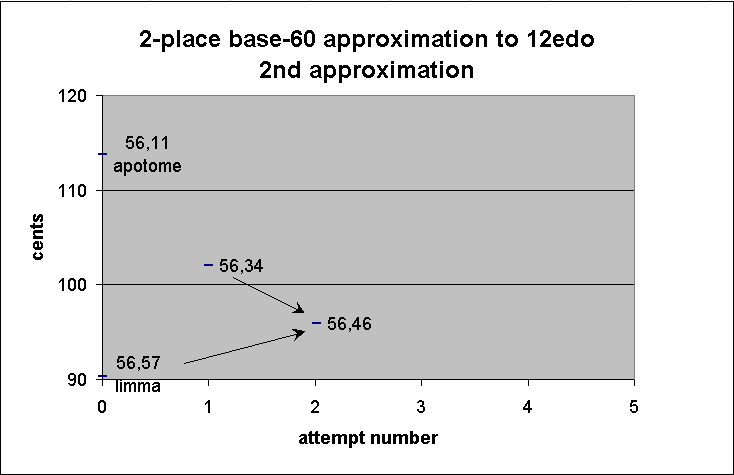
56 34 1st approximation of 12edo semitone
+ 56 57 limma
---------
1 53 31
/ 2
---------
56 46 2nd approximation of 12edo semitone
--------------- string-length -----------------
theoretical ------------- actual --------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ F#/Gb 2048/2187 56,11 3371/3600 0.936388889 113.7843351 apotome
+ F#/Gb 56,34 1697/1800 0.942777778 102.01241 1st approx. of 12edo semitone
|
|
|
+ F#/Gb 56,46 1703/1800 0.946111111 95.90216585 2nd approx. of 12edo semitone
+ F#/Gb 243/256 56,57 1139/1200 0.949166667 90.31999055 limma
Square this to check accuracy:
56 46
* 56 46
-------
~53 42
This is not as close as our last answer, so we now take
the mean between these two results:
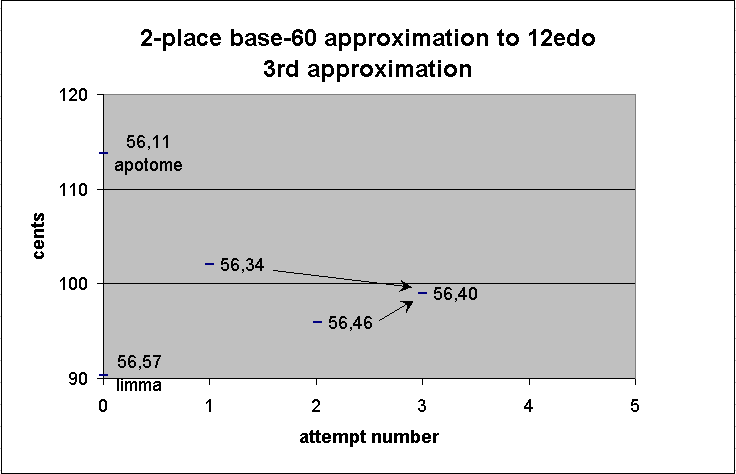
56 46 2nd approximation of 12edo semitone
+ 56 34 1st approximation of 12edo semitone
-------
1 53 20
/ 2
-------
56 40 3rd approximation of 12edo semitone
--------------- string-length -----------------
theoretical ------------- actual --------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ F#/Gb 2048/2187 56,11 3371/3600 0.936388889 113.7843351 apotome
+ F#/Gb 56,34 1697/1800 0.942777778 102.01241 1st approx. of 12edo semitone
|
|
+ F#/Gb 56,40 17/18 0.944444444 98.95459223 3rd approx. of 12edo semitone
+ F#/Gb 56,46 1703/1800 0.946111111 95.90216585 2nd approx. of 12edo semitone
+ F#/Gb 243/256 56,57 1139/1200 0.949166667 90.31999055 limma
Square it to check accuracy:
56 40
* 56 40
-------
~53 31
We'll try to get closer by taking the mean between
our two most accurate values:
56 40
+ 56 34
-------
1 53 13
/ 2
-------
~56 37
--------------- string-length -----------------
theoretical ------------- actual --------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ F#/Gb 2048/2187 56,11 3371/3600 0.936388889 113.7843351 apotome
+ F#/Gb 56,34 1697/1800 0.942777778 102.01241 1st approx. of 12edo semitone
+ F#/Gb 56,37 3397/3600 0.943611111 100.482826 4th approx. of 12edo semitone
|
+ F#/Gb 56,40 17/18 0.944444444 98.95459223 3rd approx. of 12edo semitone
+ F#/Gb 56,46 1703/1800 0.946111111 95.90216585 2nd approx. of 12edo semitone
+ F#/Gb 243/256 56,57 1139/1200 0.949166667 90.31999055 limma
Square to check accuracy:
56 37
* 56 37
-------
~53 25
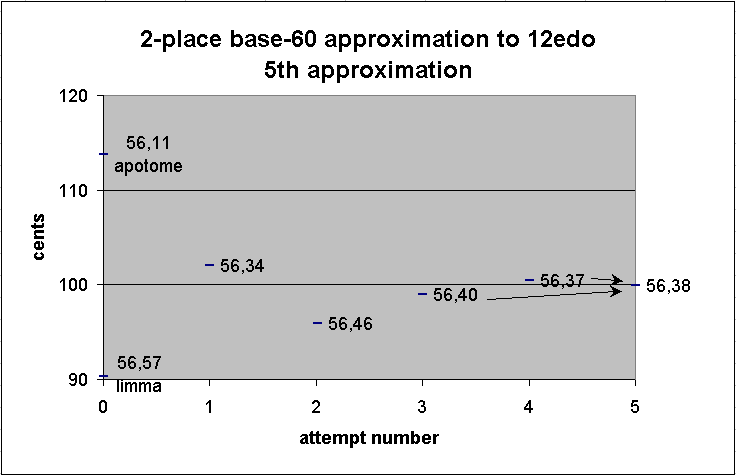
Now find the mean between these last two:
56 40
+ 56 37
-----------
1 53 17
/ 2
-----------
~56 38 30
This may be rounded either up or down; we may choose 56,38.
--------------- string-length -----------------
theoretical ------------- actual --------------
note fraction sexagesimal fraction decimal ~cents
+ ∞
.
.
.
+ F#/Gb 2048/2187 56,11 3371/3600 0.936388889 113.7843351 apotome
+ F#/Gb 56,34 1697/1800 0.942777778 102.01241 1st approx. of 12edo semitone
+ F#/Gb 56,37 3397/3600 0.943611111 100.482826 4th approx. of 12edo semitone
+ F#/Gb 56,38 1699/1800 0.943888889 99.97326484 5th approx. of 12edo semitone
+ F#/Gb 56,40 17/18 0.944444444 98.95459223 3rd approx. of 12edo semitone
+ F#/Gb 56,46 1703/1800 0.946111111 95.90216585 2nd approx. of 12edo semitone
+ F#/Gb 243/256 56,57 1139/1200 0.949166667 90.31999055 limma
Square to check accuracy:
56 38
* 56 38
-------
~53 27
Here at last we have come within 1/60 of our target value.
At ~99.97 cents, this "semitone" of 56,38 units
is certainly audibly indistinguishable from 2^(1/12).
In fact, the actual 3-place sexagesimal value for the
12-tET semitone 2^(1/12) is 56,37,57, only
3/3600 less than
our 2-place approximation.
Our hypothetical Sumerian could then easily check his
work by multiplying this value by itself 12 times, to
see how closely his final result comes to the target of
30 units.
--------- string-length ---------- ~cents error from 12edo
note sexagesimal fraction decimal ~cents decimal ~fraction
F 60 1/1 1 0 0 0
F#/Gb 56,38 1699/1800 0.943888889 99.97326484 - 0.026735161 - 1/37
G 53,27 1069/1200 0.890833333 200.1270633 + 0.12706333 + 1/8
G#/Ab 50,27 1009/1200 0.840833333 300.1298777 + 0.129877667 + 1/8
A 47,37 2857/3600 0.793611111 400.1950443 + 0.195044337 + 1/5
A#/Bb 44,57 899/1200 0.749166667 499.969662 - 0.030338022 - 1/33
B 42,26 1273/1800 0.707222222 599.7173848 - 0.282615221 - 1/4
C 40,03 267/400 0.6675 699.7923097 - 0.207690295 - 1/5
C#/Db 37,48 63/100 0.63 799.8915195 - 0.10848047 - 1/9
D 35,41 2141/3600 0.594722222 899.654533 - 0.345467002 - 1/3
D#/Eb 33,41 2021/3600 0.561388889 999.5131018 - 0.486898195 - 1/2
E 31,48 53/100 0.53 1099.122882 - 0.877117746 - 7/8
F 30,01 1801/3600 0.500277778 1199.03847 - 0.961529627 - 1
(download the Scala file)
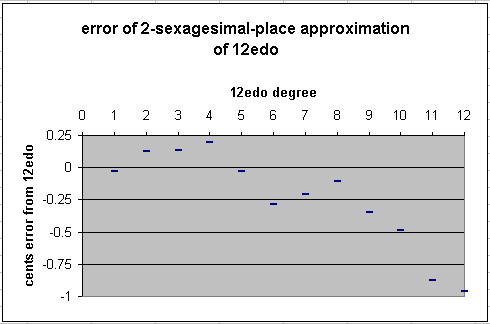
This final result is just over 1199 cents, with the
maximum error for the whole scale of ~1 cent, again, audibly
indistinguishable from the actual "8ve" under all
ordinary circumstances. Below is a graph of the
error of this approximation from true 12edo:
This can even be simplified further, by using simpler
approximations in the second sexagesimal place:
24 represents 2/5,
30 represents 1/2,
36 represents 3/5,
40 represents 2/3,
48 represents 4/5.
--------- string-length ----------
note sexagesimal fraction decimal ~cents ~cents error
F 60 1/1 0 0 0
F#/Gb 56,36 283/300 0.943333333 100.9925372 + 0.992537197
G 53,30 107/120 0.891666667 198.508331 - 1.491668951
G3/Ab 50,30 101/120 0.841666667 298.4149354 - 1.585064572
A 47,36 119/150 0.793333333 400.8011126 + 0.801112626
A#/Bb 45 3/4 0.75 498.0449991 - 1.955000865
B 42,24 53/75 0.706666667 601.0778831 + 1.077883119
C 40 2/3 0.666666667 701.9550009 + 1.955000865
C#/Db 37,48 63/100 0.63 799.8915195 - 0.10848047
D 35,40 107/180 0.594444444 900.4633319 + 0.463331914
D#/Eb 33,40 101/180 0.561111111 1000.369936 + 0.369936293
E 31,48 53/100 0.53 1099.122882 - 0.877117746
F 30 1/2 0.5 1200 0
(download the Scala file)
This results in an approximation to 12edo which has a maximum error of just under 2 cents.
So by finding successively closer approximations, by using a method of finding a mean of two known approximations and squaring or cubing that mean and comparing it to the squares or cubes of the known approximations, that's how a Sumerian could have, by hand, calculated the string-length measurements which produce a very accurate approximation of 12-tET, 5000 years ago.
See my Speculations on Sumerian Tuning for a fuller treatment of this subject. Also see my posts the the Yahoo Tuning Group in message 10930 (Mon Jun 26, 2000 11:12 pm), the footnote to message 11107 (Sat Jul 8, 2000 9:28 pm), and message 11624 (Sat Aug 19, 2000 4:48 pm) for more on Sumerian and Babylonian music.
-monz
Updated:
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by selecting the highest level of financial support that you can afford. Thank you.