Private lessons available via Discord/WhatsApp/Skype: composition, music-theory, tuning-theory, piano, and all woodwinds (sax, clarinet, flute, bassoon, recorder). Current rates US$ 80 per hour (negotiable). Send an email to: monzojoe (AT) gmail.
meantone
The term "meantone" refers to both
- a specific tuning, and
- an abstract family of temperaments, of which that tuning is a member.
1. meantone = a specific tuning
The former definiton, which has historical priority, restricts the meaning of "meantone" to specifying 1/4-comma meantone, the only tuning in which the whole-tone is exactly the geometric mean between the two normal sizes of whole-tone in 5-limit just-intonation. Some theorists prefer to restrict the meaning to only this definition. The other tunings in the family are usually called "meantone-like" by these theorists. (See the page on 1/4-comma meantone for detailed info on this specific tuning.)
2. meantone = an abstract family of temperaments
The second definition specifies the whole family of tuning-systems in which the two JI "whole tones" (with ratios of 9:8 and 10:9) are conflated into one "mean tone" which lies somewhere in size between those two, the objectives being to produce or approximate JI "major-3rd"s (which have a ratio of 5:4) but simultaneously to eliminate the syntonic-comma and its associated problem of commatic drift, by having only one size of whole-tone. During the late 1900s most tuning theorists accepted "meantone" to describe the whole family of temperaments -- that is, all temperaments in which the syntonic-comma vanishes.
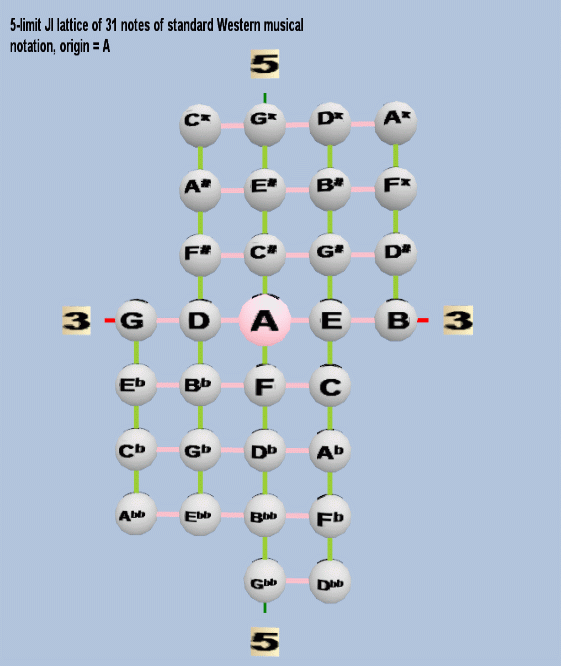
Meantones are always considered to be octave-equivalent -- thus, the lattice essentially ignores prime-factor 2, requiring only axes for 3 and 5. Here is a rectangular lattice of this 2-dimensional prime-space into which the ratios of 5-limit JI may be embedded (in this example the origin = "A"); on both lattices, pink connectors illustrate instances of the 3-axis, and green connectors illustrate instances of the 5-axis:
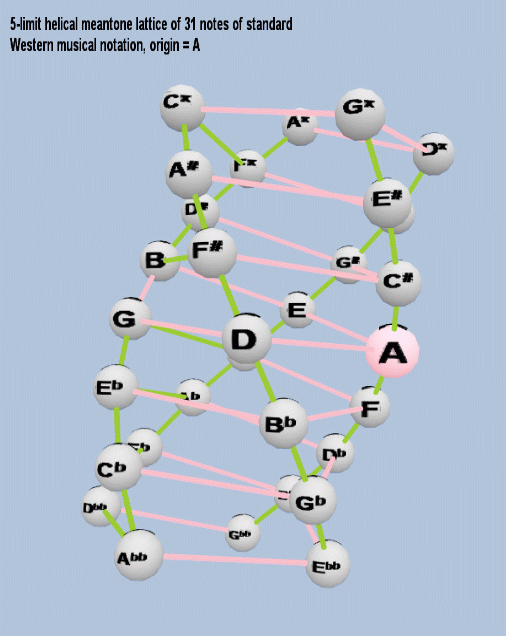
In terms of this prime-space, the lattice describing meantone twists the axes into a 4-strand helix where the spot occupied by 34 is in exactly the same place as the spot occupied by 51 ("C#" in this example). On the meantone helical lattice it can be seen that all of the axes in the rectangular lattice become spirals: the green 5-limit axes form the four twisted strands of the helix, and the pink 3-limit axes form one long tight spiral connecting the four strands together.
As with pythagorean tuning, meantone is a chain-of-5ths type of tuning, in which the generator of the chain is the "perfect-5th" (or equivalently but with opposite sign, the "perfect-4th"). By narrowing the just 3:2 by a distributed fraction of the syntonic-comma, after cycling thru the chain a number of generators equal to the denominator of the fraction of the tempering, one arrives at a pitch exactly one syntonic-comma lower than the one which would occupy the spot of that number on the 3-axis of a lattice. For example, using "A" as the origin (1:1 ratio):
- in 1/3-comma meantone: E is 1/3-comma narrow, B is 2/3-comma narrow, and F# is 3/3 = 1 comma narrow, which places it directly onto another 5-axis, ratio 5/3;
- in 1/4-comma meantone: E is 1/4-comma narrow, B is 2/4 = 1/2-comma narrow, F# is 3/4-comma narrow, and C# is 4/4 = 1 comma narrow = ratio 5/4;
- in 1/6-comma meantone: E is 1/6-comma narrow, B is 2/6 = 1/3-comma narrow, F# is 3/6 = 1/2-comma narrow, C# is 4/6 = 2/3-comma narrow, G# is 5/6-comma narrow, and D# is 6/6 = 1 comma narrow = ratio 45/32
The fraction of a syntonic-comma tempering of the generator "5th" is generally used as part of the name of the tuning -- thus the names "quarter-comma meantone", "2/7-comma meantone", etc; this stems from a usage by J. M. Barbour in 1951 of such terms as "2/7-comma temperament" etc., but Barbour was always careful to use meantone only as in definition #1, and always called these other versions "varieties of meantone temperament".
Of course, it is not necessary that the amount of tempering be a rational part of the comma -- thus, we have various types of approximations to these theoretical ideals:
- EDOs which are close in tuning to fraction-of-a-comma meantones (some theorists prefer to refer to them as ETs for this reason);
- TOP meantone, which also tempers the octaves; and
- LucyTuning, based on pi, and which is actually not considered by Charles Lucy to represent fraction-of-a-comma meantone.
The elimination of the syntonic comma determines the essential features of meantone systems:
- the equation of the "major-3rd" with four "5ths", and
- a single size of whole-tone, two of which compose that major-3rd.
Note that while ET versions of meantone create a closed (circular) system, the non-ET meantones (i.e., all of the fraction-of-a-comma meantones) do not. They instead form an open-ended chain.
meantone basis of standard music-theory
One important point to make is that our standard music-theory is based on meantone: harmony is generally considered to have some resemblance to 5-limit JI, but there is always only one size of whole-tone.
Our standard musical notation evolved c.1000 for pythagorean tuning (first in the "dialogus" of pseudo-Odo), but because of the fact that meantone can be characterized as a chain-of-5ths with exactly the same notation as pythagorean, when 5-limit JI was recognized as a kind of theoretical ideal c.1480 (first by Ramos) and then shortly afterwards (c.1510) 1/4-comma-meantone was accepted as a practical temperament of that JI (see Aron's "Toscanello", last section of the webpage), the same notation was easily adapted to the meantone tuning.
First, observe that in "common-practice" (c.1600-1900) compositions and theory, a distinction is never made between nominals which have the same letter: i.e., all "A"s are the same, all "B"s, etc. This means that the syntonic-comma difference in pitch is not recognized -- and thus, that the promo with the 2,3,5-monzo [-4 4, -1> vanishes.
Secondly, the current standard 12-edo tuning -- while it too emulates a specific form of meantone (1/11-comma) -- also tempers out an additional unison-vector (the enharmonic diesis), causing it to exhibit enharmonic equivalence for pairs of notes which are written ("spelled") differently (i.e., A# = Bb). Thus, most people tend to think of these pairs of notes as being the same, which they actually are in 12-edo.
But all other meantones have distinctive pairs of pitches for these pairs of notes, so that they are not exactly the same. As the fraction-of-a-comma tempering becomes larger than 1/11, the difference between notes which are considered enharmonically equivalent in 12-edo becomes greater. At 19-edo (~=1/3-comma), the whole-tone is divided evenly into 3 parts, so that A# and Bb, for example, are as far apart from each other as they are from their respective neighbors in the diatonic scale -- so it barely makes sense to refer to them as "semitones" at all in this case, because they are quite literally "1/3-tones". (Some comparisons may be viewed on this mouse-over applet.)
All meantones except 12-edo thus make a distinction between two different kinds of "half-step" or semitone:
- The interval between a nominal, and a note with the same nominal but an additional sharp or flat, is called a chromatic-semitone or augmented prime. (i.e., A:A#, B:Bb, etc.)
- The interval between a nominal, and either the next nominal above it but with an additional flat, or the next nominal below it with an additional sharp, is called a diatonic-semitone or minor 2nd. (i.e., A:Bb, A#:B, etc.)
5-limit meantone systems are linear-temperaments, and are most often used with a cardinality of 12 notes, in a chain of tempered-"5th" generators named thus:
Eb -- Bb -- F -- C -- G -- D -- A -- E -- B -- F# -- C# -- G#
The interval G#:Eb is called the wolf, is classified as a "diminished-6th", and in most meantones is significantly wider than the size of the generator but close enough to it to sound like a mistuned "5th", and in most meantones is also highly discordant. Its complement is the "wolf 4th" Eb:G#, which is technically an "augmented-3rd".
Along with the naming of the notes, the qualifiers in the descriptive names of the intervals ("major", "minor", "augmented", "diminished") are also based on this paired-semitone notation.
It was primarily the prominence of the Halberstadt keyboard which caused most musicians to want to limit the meantone chain to 12 notes, but there have been many experiments with keyboards designed to accomodate more notes per octave, giving a longer meantone chain.
algebra of meantone interval calculation
All of the main intervals in any meantone may be computed algebraically as combinations of the three basic intervals, which have these relationships:
s' = augmented-prime = t - s = chromatic semitone s = minor-2nd = t - s' = diatonic semitone t = major-2nd = s + s' = tone (whole-tone) (note that in the case of 12-et s = s', and in the case of 19-et s = 2s')
The set of intervals generally found in all meantones is thus:
perfect-8ve = 5t + 2s diminished-8ve = 4t + 3s augmented-7th = 6t major-7th = 5t + s minor-7th = 4t + 2s diminished-7th = 3t + 3s augmented-6th = 5t major-6th = 4t + s minor-6th = 3t + 2s diminished-6th = 2t + 3s augmented-5th = 4t perfect-5th = 3t + s diminished-5th = 2t + 2s augmented-4th = 3t perfect-4th = 2t + s diminished-4th = t + 2s augmented-3rd = 2t + s' major-3rd = 2t minor-3rd = t + s diminished-3rd = 2s augmented-2nd = t + s' major-2nd = t minor-2nd = s diminished-2nd = s - s' augmented-prime = s' perfect-prime = 0
meantone mapping of prime-factors above 5
While the whole point of meantones, as explained above, is to collapse the 2-dimensional octave-equivalent 5-limit lattice into a 1-dimensional linear temperament which emulates (in notation, but not in tuning) the linear pythagorean system, it so happens that certain meantones can provide very good approximations to higher odd/prime limits.
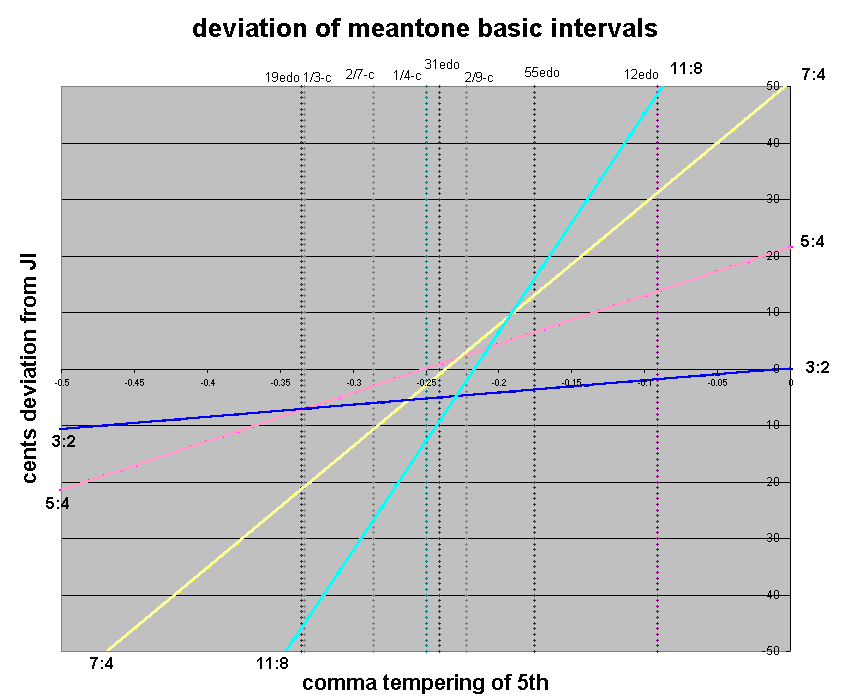
Below is a graph showing the deviation of the basic intervals in meantone from their just intonation equivalents in the 11-limit. The horizontal axis represents the fraction-of-a-comma amount by which the meantone generator (i.e., the "5th") is tempered (narrowed) from the pythagorean "pure 5th" of ratio 3:2. The vertical axis shows the deviation in cents from the JI intervals, of 1 generator from 3:2 (blue line), 4 generators (octave-equivalent) from 5:4 (pink), 10 generators from 7:4 (yellow), and 18 generators from 11:8 (cyan). Some common meantones are drawn vertically as illustrations. (In this graph an alternative mapping of 11:8, to -13 generators, is not shown. All of these graphs choose one particular mapping of 11-limit ratios, as shown at the bottom of the "meantone error" applet which can be viewed by clicking on the small graph below.)
Below is a graph showing the average absolute deviation for each set of ratios of prime-factors.
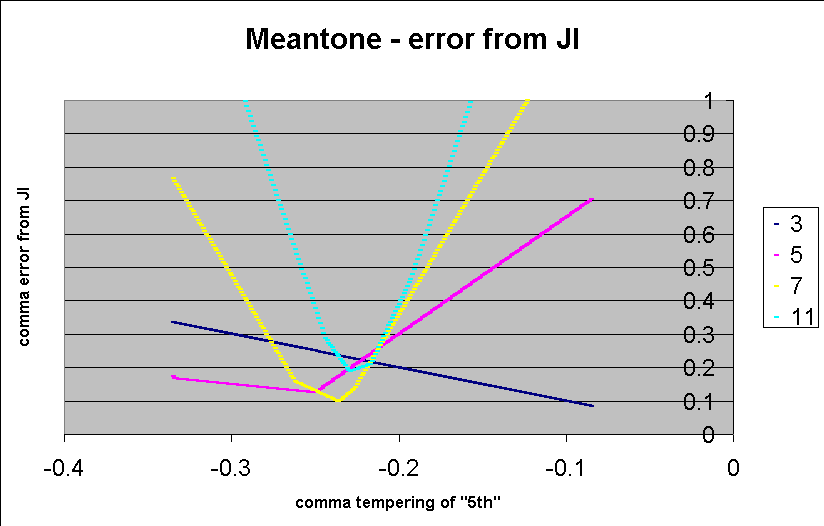
Below is a closeup of the central section from the above graph.
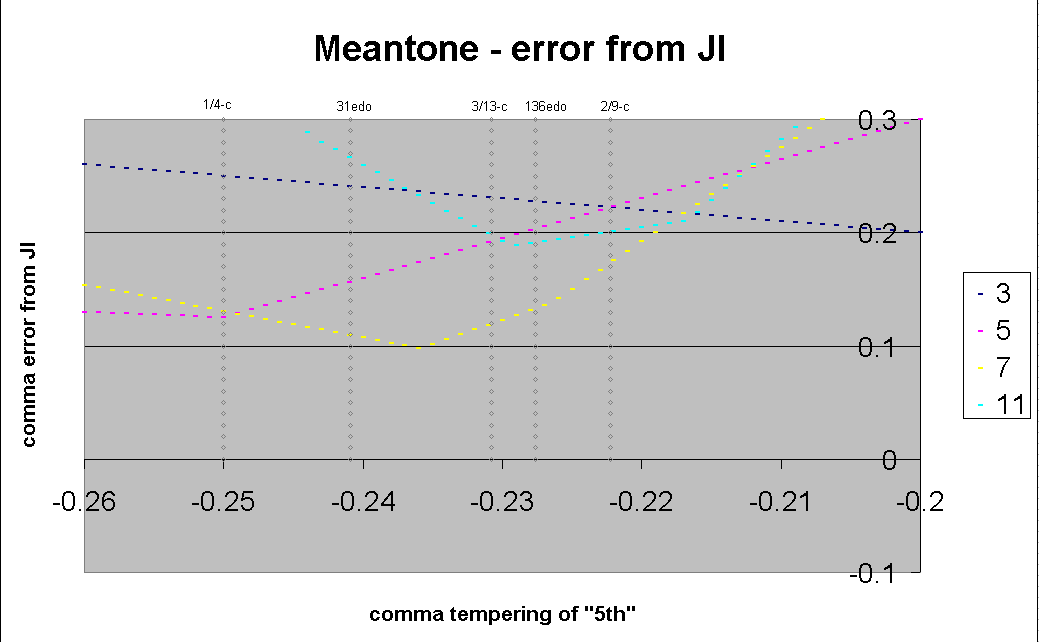
If one follows Partch's observation that the sensitivity of a ratio to mistuning is directly proportional to its prime- (or odd-) limit, it can be seen from the above graph that the area between 0.229- and 0.217-comma meantone is pretty close to ideal for a meantone representing 11-limit harmony using the mapping I chose.
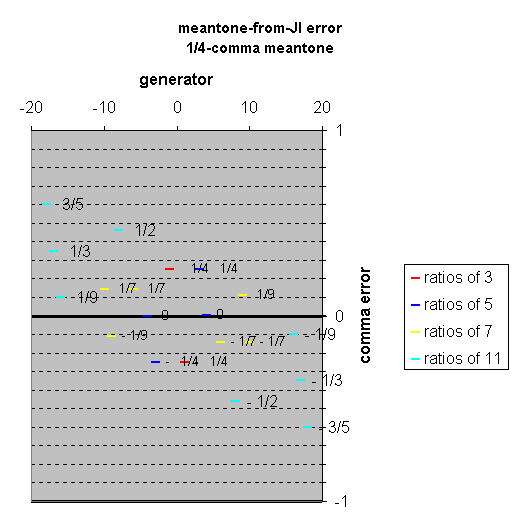
|
Click on the graphic at left to open a new window with a mouse-over applet which shows the error of various specific meantones from JI. |
On 2004.07.17, Gene Ward Smith pointed out that this mapping is the "huygens" meantone mapping, and that an error graph for the meantone/meanpop mapping should also be included for comparison. Here are new versions of both; the only difference is in the mapping of 11 -- note that both mappings are equivalent in 31-edo (mouse-over the links to see the graph):

Comments from John Chalmers on meantone
...the definition of meantone could be tightened up a bit as it implies that all meantone-like tunings have 5/4 major thirds. I would describe meantone [that is, meantone proper] as the temperament whose fifth is equal to the fourth root of 5 and is thus 1/4 of a syntonic comma flatter than 3/2.
Meantone-like temperaments are those cyclic systems which have fifths flatter than 3/2 by some fraction (rational or irrational) of the syntonic comma and which form their major thirds by four ascending fifths reduced by two octaves. Such tunings divide the ditone (which is here equivalent to the major third) into two equal "mean tones" Well-known examples include the 1/3-comma (just 6/5 and 5/3), the 1/5-comma (just 15/8, 16/15), and John Harrison's tuning whose major third equals 2(1/pi) and which has been revived and promoted in an extended form by Charles Lucy.
Certain meantone-like temperaments are audibly equivalent to equal temperaments of the octave. For example, the 1/4-comma system corresponds to 31-tet and the 1/3 comma to 19-tet. Arbitrarily close equivalences may be found by using continued fractions or Brun's Algorithm.
The upper limit of meantone-like fifths is the fifth of 12-tone ET (700 cents) and the upper limit of meantone-like major thirds is the major third of 12-tet (400 cents).
(While pythagorean tuning could be considered as a meantone-like system in which the tempering fraction is zero, temperaments whose fifths are larger than 700 cents are best thought of as positive systems, which make their major thirds by a chain of 8 descending fifths (or ascending fourths). These major thirds are formally diminished fourths (e.g., C-Fb). Other relations occur as the fifth become still sharper (9 fifths up, augmented second, C-D#).)
historical summaries of meantone tunings
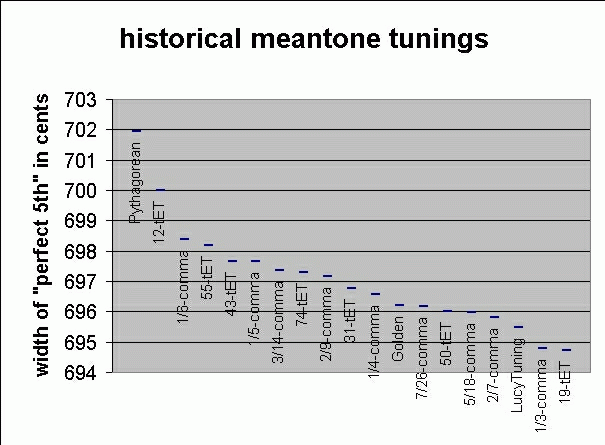
Here is a summary of the meantone tunings (giving the size of fifth in cents, the fraction of the syntonic comma by which the fifth is reduced, and the first known advocate or reference to a TD posting by me from Brett Barbaro's e-mail) that are optimal under various error criteria for the three "classical" consonant interval classes: the one 3-limit interval, the p4/p5; and the two 5-limit intervals, the m3/M6 and the M3/m6.
| Max. error |Sum-squared error|Sum-absolute error|
---------+------------+-----------------+------------------+
Inverse | 697.3465 | 696.5354 | 696.5784 |
Limit | 3/14-comma | 63/250-comma | 1/4-comma |
Weighted | Riccati |TD 162.10 5/5/99 | Aron |
---------+------------+-----------------+------------------+
Equal | 696.5784 | 696.1648 | 696.5784 |
Weighted | 1/4-comma | 7/26-comma | 1/4-comma |
| Aron | Woolhouse | Aron |
---------+------------+-----------------+------------------+
Limit | 695.9810 | 696.0187 | 696.5784 |
Weighted | 5/18-comma | 175/634-comma | 1/4-comma |
| ~Smith | Erlich (TTTTTT) | Aron |
---------+------------+-----------------+------------------+
m3/M6 & | 695.8103 | 695.9332 | 696.5784 |
M3/m6 | 2/7-comma | 7/25-comma | 1/4-comma |
only | Zarlino | This may be new | Aron |
---------+------------+-----------------+------------------+
Summary of historical meantone tunings
[ranked by size of '5th']
Variety Theorist Date Minor Third Major Third Fifth
pythagorean Ling Lun c.2000BC 294.13 ¢ 407.82 ¢ 701.96 ¢
12-tET Chu Tsai-yü 1596 300.00 400.00 700.00
1/6-comma Silbermann <1748 304.89 393.48 698.37
55-tET Beer <1722 305.45 392.73 698.18
43-tET Sauveur 1701 306.98 390.70 697.67
1/5-comma Verheyen c.1600 307.04 390.62 697.65
Sauveur 1701
3/14-comma Riccati 1762 307.96 389.39 697.35
74-tET Riccati 1762 308.11 389.19 697.30
2/9-comma Rossi 1666 308.47 388.70 697.18
Drobisch 1855
31-tET *Vicentino 1555 309.68 387.10 696.77
1/4-comma *Aron 1523 310.26 386.31 696.58
Golden Kornerup 1930 311.36 384.86 696.21
7/26-comma Woolhouse 1835 311.51 384.66 696.16
50-tET Henfling 1710 312.00 384.00 696.00
5/18-comma Smith 1749 312.06 383.92 695.98
2/7-comma Zarlino 1558 312.57 383.24 695.81
LucyTuning Harrison 1775 313.52 381.97 695.49
1/3-comma Salinas 1577 315.64 379.15 694.79
19-tET Costeley 1558 315.79 378.95 694.74
1/2-comma Fogliano 1529 326.39 364.81 691.20
* For some cautionary annotations by Margo Schulter concerning Aron and Vicentino in this table, see her Tuning List posting of Sun Feb 13, 2000 11:24pm, which appeared in Onelist Tuning Digest # 532, message 12.
Note also that while Aron was the first theorist to give a thorough description of 1/4-comma meantone, Arnold Schlick was the first to desribe to describe it at all, in 1511 [Schlick, Arnold. Spiegel der Orgelmacher und Organisten. Speyer, 1511. Monatshefte für Musikgeschichte, Heidelberg, 1869. Reprint 1959. English translation by E.B. Barber, Frits Knuf, Buren, 1980.]. See this German webpage.


|
Click on the image at left to open a window with animated graphs comparing various meantone chains. |
meantone coincidences of just intonation interval chains
Meantone cycles which are based on tempering by a fraction of a syntonic comma, which is a 5-limit interval, can have some of their pitches graphed on a lattice diagram. (I explained the mathematics of one example of this -- 1/6-comma meantone equating to a cycle of 64:45's -- in Yahoo Tuning List message #30125, (Tue Nov 13, 2001 6:55 am)).
Below is a 5-limit lattice illustrating partial cycles of the most common meantone tunings; the cell containing the reference pitch "C" is colored black because all the cycles contain it, and thus all the axes which represent the different cycles pass thru and are centered on that point on the lattice.
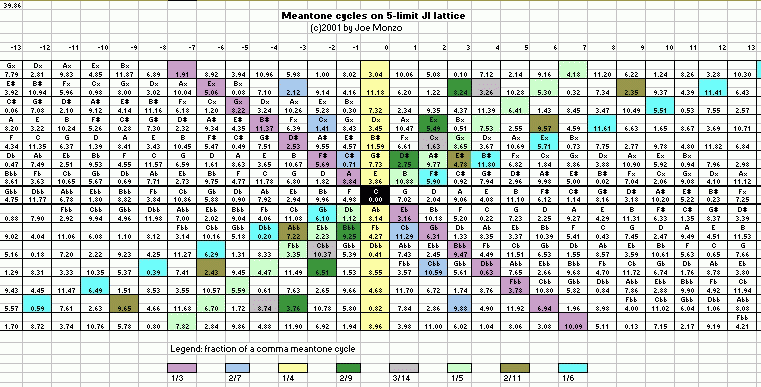
Applet: meantone tunings approximating JI-interval cycles
Below is an applet illustrating several examples of the chains on the above diagram.
MouseOver the names of the various fraction-of-a-comma meantone chains to see a graph of the notes on a 5-limit lattice diagram. Each blue square on the graph represents a "cell" or ratio-point on the lattice, with powers of 3 along the horizontal axis and powers of 5 along the vertical axis. The plots of these cells gives each meantone cycle a unique angle and density.
The ratios of generator g in n/d-comma meantone are plotted as 3x * 5y, where x = (d-(4*n))*g and y = n*g.
These meantone chains can be approximated arbitrarily closely by various EDO cycles, for example, 1/3-comma equates to 19-EDO (generators -9 to +9), 1/4-comma to 31-EDO (generators -15 to +15), 1/5-comma to 43-EDO (generators -21 to +21), 1/6-comma to 55-EDO (generators -27 to +27), 1/11-comma to 12-EDO (generators -6 to +5 or -5 to +6), etc. I have not taken this into account on these graphs, and simply arbitrarily extend each cycle from -22 to +22 generators.
Meantones as JI-interval chains
1/2 1/3 2/7 5/18 7/26 1/4 2/9 3/14 1/5 2/11 3/17 1/6 1/11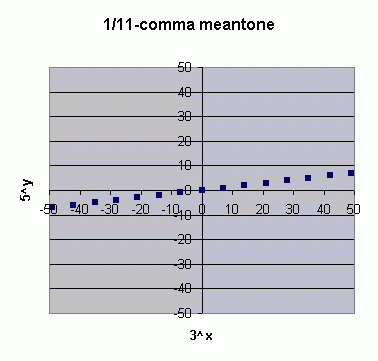
I expanded on the above idea to create a set of diagrams which I think are really useful: Lattice diagrams comparing rational implications of various meantone chains.
Below are some crude ASCII lattice diagrams which accurately portray the nature of meantone intervallic relationships. These are flat projections of what are intended to be cylindrical diagrams. The dotted line represents a circle whereby pitches wrap around the cylinder to occupy the same point.
Here is the meantone diatonic C-major scale:
,,-F
,,-C-'' / \
,,-G-'' / \ / \
..D-''../.\.../...\./..,,-D..
\ / \ / ,,-A-''
\ / ,,-E-''
B-''
Here is a typical 12-tone meantone system:
,,-Eb
,,-Bb'' / \
..F-''.../.\.../...\....,,-F..
\ / \ / ,,-C-'' / \
\ / ,,-G-'' / \ / \
..D-''../.\.../...\./..,,-D..
\ / \ / ,,-A-'' / \
\ / ,,-E-'' / \ / \
..B-''../.\.../...\./...,,-B..
\ / \ / ,,-F#-''
\ / ,,-C#-''
..G#-''
And meantones may also be found with pitch-sets larger than 12 notes, thus:
,,-Fb
..Cb''.../.\...........,,-Cb..
\ / \ ,,-Gb'' / \
\ / ,,-Db'' / \ / \
..Ab''.../.\.../...\./..,,-Ab..
\ / \ / ,,-Eb'' / \
\ / ,,-Bb'' / \ / \
..F-''.../.\.../...\./..,,-F..
\ / \ / ,,-C-'' / \
\ / ,,-G-'' / \ / \
..D-''../.\.../...\./..,,-D..
\ / \ / ,,-A-'' / \
\ / ,,-E-'' / \ / \
..B-''../.\.../...\./...,,-B..
\ / \ / ,,-F#-'' / \
\ / ,,-C#-'' / \ / \
..G#-''./.\.../...\./..,,-G#..
\ / \ / ,,-D#'' / \
\ / ,,-A#-'' / \ / \
..E#''../.\.../...\./..,,-E#..
\ / \ / ,,-B#'' / \
\ / ,,-Fx'' / \ / \
..Cx''../.\.../...\./..,,-Cx..
\ / \ / ,,-Gx''
\ / ,,-Dx''
..Ax''
The proper way to lattice a meantone, or any linear temperament, is as a cylinder which runs perpendicular to the vector of the interval being tempered out. Here is a Monzo lattice of 1/4-comma meantone, with a typcial 12-tone Eb...G# scale showing along the meantone chain on the face of the cylinder.
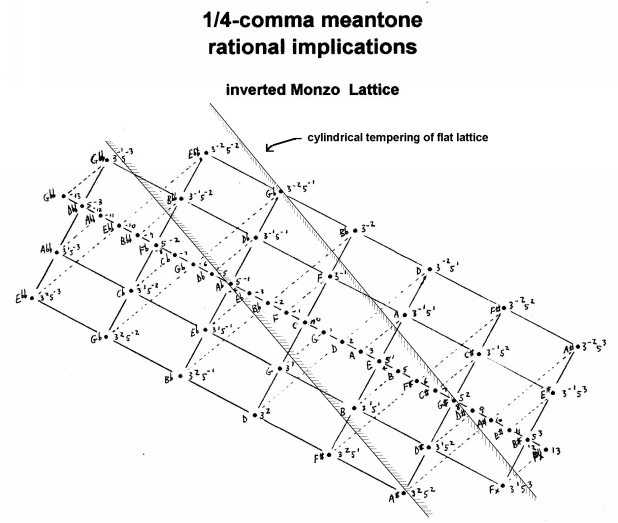
The cylinder for all meantones will always have the same angle to the lines on my JI lattice, because they all temper out the same interval, the syntonic comma. On my lattices, each meantone chain itself will spiral around the cylinder differently depending on the fraction of a comma by which the "5th" is tempered.
Tonescape™ meantone lattice
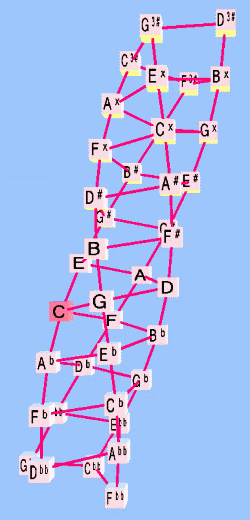
helical lattice diagrams of open-ended meantones
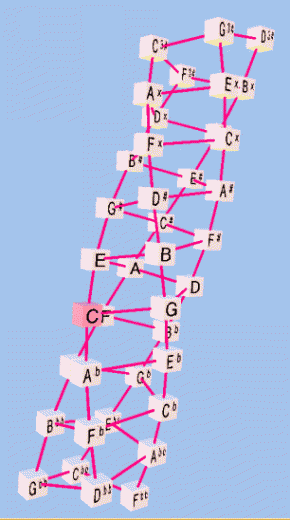
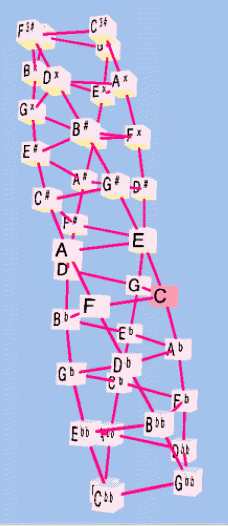
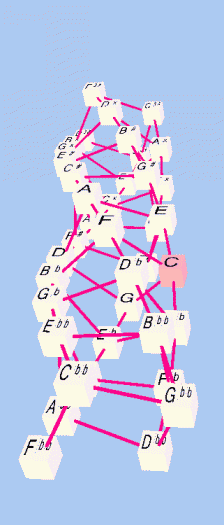
Below is a version of the 4-strand helical meantone Musica lattice showing four different rotations of the view. The reference pitch is C n0.
- The 4 strands represent 4 different chains of approximations to the 5:4 ratio (major-3rds). With prime-factorization, this represents steps of 5+/- 1. Thus, one chain can be read (from the bottom up) as Dbb - Fb - Ab - C - E - G# - B#, etc., another chain as Fbb - Abb - Cb - Eb - G - B - D# - Fx, etc., and so on.
- The connectors between the strands form a spiral which represents a single chain of approximations to the 3:2 ratio ("perfect-5th"). With prime-factorization, this represents steps of 3+/- 1. This chain can be read from the bottom of the lattice as Fbb - Cbb - Gbb - Dbb - Abb - Ebb - Bbb - Fb, etc., continuing the spiral all the way to the top at "D3#".
- It is easy to follow the progression of generator "5ths" around the spiral and see that on this lattice 34 = 51, the essential meantone equation.
 |
 |
 |
 |
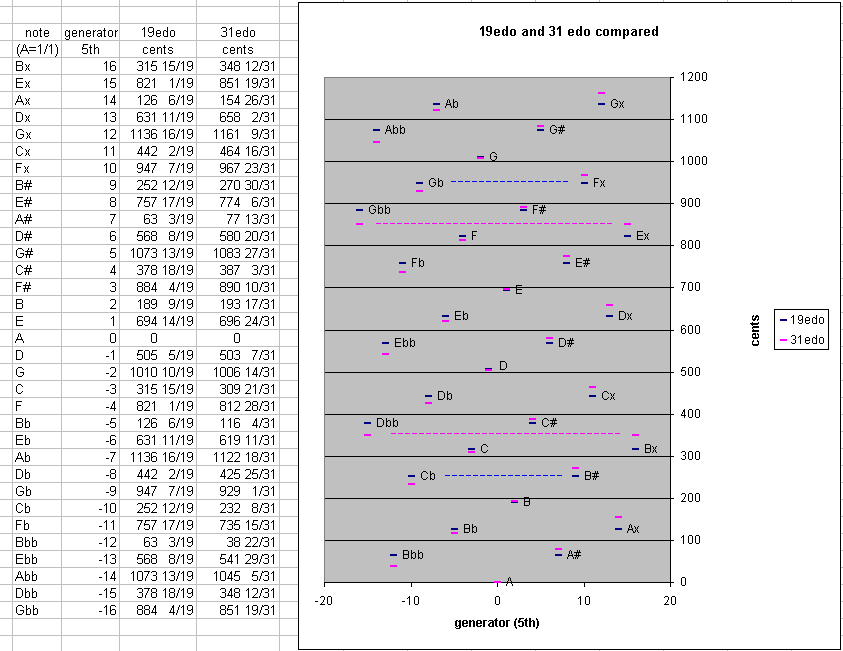
Comparison of 19edo and 31edo
Two of the earliest, commonest, and most convenient forms of meantone tuning are 19-edo and 31-edo. Below is a table and graph comparing their "cycle of 5ths".
Meantone family data
abstract data
| family name: | meantone |
| period: | octave |
| generator: | a flat 5th or sharp 4th |
5-limit
| name: | meantone, 12&19 |
| comma: | 81/80 ratio = 2,3,5-monzo |-4 4, -1> = syntonic-comma |
| mapping: | [<1 2 4|, <0 -1 -4|] |
| poptimal generator: | 34/81-edo |
| MOS cardinalities: | 5, 7, 12, 19, 31, 50, 81 |
7-limit
| name: | meantone, standard septimal meantone, 12&19 |
| wedgie: | <<1 4 10 4 13 12|| |
| mapping: | [<1 2 4 7|, <0 -1 -4 -10|] (fourth generator) |
| 7&9 limit copoptimal generator: | 5^(1/4) fifth (1/4 comma meantone) |
| 7 limit poptimal: | 86/205-edo |
| 9 limit poptimal: | 47/112-edo |
| TM basis: | {81/80, 126/125} ratios |
| MOS cardinalities: | 5, 7, 12, 19, 31, 50, 81 |
| name: | dominant, dominant sevenths, 5&12 |
| wedgie: | <<1 4 -2 4 -6 -16|| |
| mapping: | [<1 2 4 2|, <0 -1 -4 2|] |
| 7&9 limit copoptimal generator: | 29/70-edo |
| TM basis: | {36/35, 64/63} ratios |
| MOS cardinalities: | 5, 7, 12, 17, 29 |
| name: | flattone, 19&26 |
| wedgie: | <<1 4 -9 4 -17 -32|| |
| mapping: | [<1 2 4 -1|, <0 -1 -4 9|] |
| 7 limit poptimal generator: | 46/109-edo |
| 9 limit poptimal generator: | 27/64-edo |
| TM basis: | {81/80, 525/512} ratios |
| MOS cardinalities: | 5, 7, 12, 19, 26, 45 |
11 limit
| name: | meantone, meanpop, 19&31 |
| wedgie: | <<1 4 10 -13 4 13 -24 12 -44 -71|| |
| mapping: | [<1 2 4 7 -2|, <0 -1 -4 -10 13|] |
| poptimal generator: | 47/112-edo |
| TM basis: | {81/80, 126/125, 385/384} ratios |
| MOS cardinalities: | 5, 7, 12, 19, 31, 50, 81 |
| name: | huygens, fokker, 12&31 |
| wedgie: | <<1 4 10 18 4 13 25 12 28 16|| |
| mapping: | [<1 2 4 7 11|, <0 -1 -4 -10 -18|] |
| poptimal generator: | 13/31-edo |
| TM basis: | {81/80, 126/125, 99/98} ratios |
| MOS cardinalities: | 5, 7, 12, 19, 31, 43 |
| name: | meanertone |
| wedgie: | <<1 4 3 -1 4 2 -5 -4 -16 -13|| |
| mapping: | [<1 2 4 4 3|, <0 -1 -4 -3 1|] |
| poptimal generator: | 13/31-edo |
| TM basis: | {21/20, 28/27, 33/32} ratios |
| MOS cardinalities: | 5, 7, 12, 19, 31, 43 |
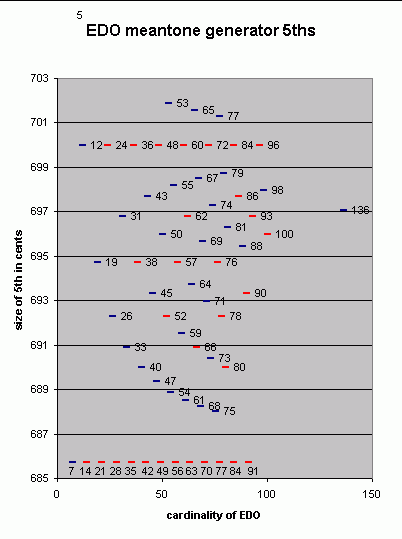
|
~cents deg / card *2 *3 *4 720 3 / 5 701.8867925 31 / 53 701.5384615 38 / 65 701.2987013 45 / 77 700 7 / 12 14 / 24 21 / 36 28 / 48 698.7341772 46 / 79 698.5074627 39 / 67 698.1818182 32 / 55 697.9591837 57 / 98 697.6744186 25 / 43 50 / 86 697.2972973 43 / 74 697.0588235 79 / 136 696.7741935 18 / 31 36 / 62 54 / 93 696.2962963 47 / 81 696 29 / 50 58 / 100 695.6521739 40 / 69 695.4545455 51 / 88 694.7368421 11 / 19 22 / 38 33 / 57 44 / 76 693.75 37 / 64 693.3333333 26 / 45 52 / 90 692.9577465 41 / 71 692.3076923 15 / 26 30 / 52 45 / 78 691.5254237 34 / 59 690.9090909 19 / 33 38 / 66 690.4109589 42 / 73 690.0 23 / 40 46 / 80 689.3617021 27 / 47 688.8888889 31 / 54 688.5245902 35 / 61 688.2352941 39 / 68 688.0 43 / 75 685.7142857 4 / 7 8 / 14 12 / 21 16 / 28 |
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.
