Hindemith's 5-limit just intonation derivation
of 12-tone equal temperament

Paul Hindemith, in his book The Craft of Musical Composition, volume 1, describes a derivation of 12-et as a tempering of a 12-tone just intonation scale, which in turn is generated as subharmonics of higher partials.

In Genesis of a Music (p 420 in the 2nd edition), Harry Partch provides an informative diagram which succinctly illustrates Hindemith's explanation.

Below is a 3-dimensional Musica lattice in 2,3,5-prime-space, showing the same data as Partch's diagram.

• The black lines represent the axes of the prime-factors 2, 3, and 5.
• The maroon lines are connectors which are parallel to those axes.
• The white cubes are the notes which are the higher partials, and which Hindemith says generate the scale.
• The orange cubes are the scale notes.
• The blue lines show the derivation of scale notes from higher partials, as described by Hindemith

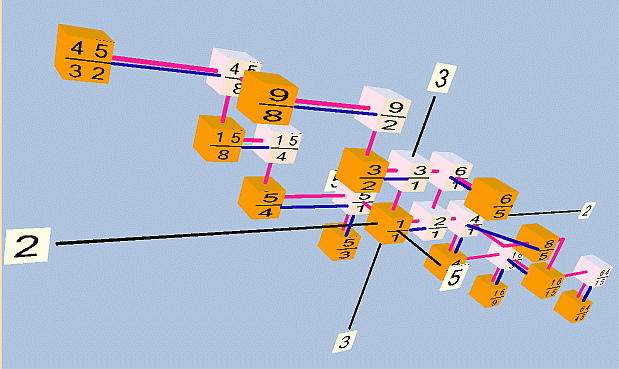
Below is the data for the above lattice, showing each pair of notes group together: the higher partial (white lattice cube) comes first, then below it is the generated scale note (orange cube).

  2,3,5-monzo      ratio   partial

[ 1   0,   0 >     2 / 1    2
[ 0   0,   0 >     1 / 1    1

[ 0   1,   0 >     3 / 1    2
[-1   1,   0 >     3 / 2    1

[ 2   0,   0 >     4 / 1    3
[ 2  -1,   0 >     4 / 3    1

[ 0   0,   1 >     5 / 1    3
[ 0  -1,   1 >     5 / 3    1

[ 0   0,   1 >     5 / 1    4
[-2   0,   1 >     5 / 4    1

[ 1   1,   0 >     6 / 1    5
[ 1   1,  -1 >     6 / 5    1

[ 2   0,   0 >     4 / 1    5
[ 3   0,  -1 >     8 / 5    2    NOTE: involves 2 prime-factors, so blue line is angled

[-1   2,   0 >     9 / 2    4
[-3   2,   0 >     9 / 8    1

[ 4  -1,   0 >    16 / 3    3
[ 4  -2,   0 >    16 / 9    1

[ 4  -1,   0 >    16 / 3    5
[ 4  -1,  -1 >    16 / 15   1

[-2   1,   1 >    15 / 4    2
[-3   1,   1 >    15 / 8    1

[ 6  -1,  -1 >    64 / 15   3
[ 6  -2,  -1 >    64 / 45   1

[-3   2,   1 >    45 / 8    4
[-5   2,   1 >    45 / 32   1
		

Partch notes that Hindemith confounds the last two scale-notes into one.

It can be seen that the scale shown in orange on the lattice is exactly the same as the "closest to 1/1" 12-et bingo-card tiling derived by Joe Monzo.

It seems to me all that is being said here is that

1. 12-et can be described as a tempering of the Malcolm Monochord or its inverse, New Albion.
2. The fundamental theorem of arithmetic -- that any positive rational number can be uniquely factored into primes -- is really true.

There's also a suggestion that Hindemith is willing, Peter Sault style, to switch between Malcolm and New Albion.

Point number one is of course true for any epimorphic 12-scale, and point number two removes any necessity of showing that a rational number is the product of primes in any particular case, since this is always true.

The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.

support level

donor: $5 USD friend: $25 USD patron: $50 USD savior: $100 USD angel of tuning: $500 USD microtonal god: $1000 USD