| family name: | marvel |
| generators: | 2, 3, 5 |
| name: | marvel |
| comma: | 225/224 |
| mapping: | [<1 0 0 -5], <0 1 0 2|, <0 0 1 2|] |
| TOP tuning: | [1200.494, 1901.173, 2785.167, 3370.212] |
| possible et tunings: |
|
| other tunings: |
|
| supporting linear temperaments: |
|
| name: | marvel |
| commas: | {225/224, 385/384} |
| planar wedgie: | <<<1 2 -3 -2 1 -4 -5 12 9 -19||| |
| mapping: | [<1 0 0 -5 12|, <0 1 0 2 -1|, <0 0 1 2 -3|] |
| TOP tuning: | [1200.509, 1901.149, 2785.133, 3370.019, 4149.558] |
| possible et tunings: | 72, 238, 310 |
| minimax tuning: |
(26873856/1375)^(1/9) for 3, (2097152000/1089)^(1/9) for 5 |
| supporting temperaments: |
|
| name: | prodigy |
| commas: | {225/224, 441/440} |
| planar wedgie: | <<<1 -2 3 -2 6 -6 5 -13 11 -4||| |
| mapping: | [<1 0 0 -5 -13|, <0 1 0 2 6|, <0 0 1 2 3|] |
| TOP tuning: | [1200., 1900.058168, 2783.119618] |
| possible et tunings: | 72, 780 |
| supporting temperaments: |
|
Here is an example of one marvel tuning:
... here is a 31-note scale called keenan5, which I decided to reverse engineer. It is not a random collection of notes; it does not even have a complex structure like a ciculating temperament often will. It is straightforward, logical, and yes, mathematical in the way it was evidently constructed.
By running it through Scala's equal temperament fitter, I found it could be fitted, increasingly well, to 31, 41, 72, 125 and 166. This strongly suggests it is 11-limit marvel, which you can discover by putting together the corresponding standard vals.
By fitting it to 166-equal, and then replacing the steps of size 4, 5, and 7 with steps of size 2048/2025, 16875/16384 and 128/125, I produced an algebraically exact 5-limit version. This does exactly what Dave objects to, namely, exhibits the scale as a planar temperament. Approximations to 2,3 and 5 can be used to generate marvel, and hence the 5-limit version tells you what the mapping from 11-limit JI is--the thing I was calling the temperament itself. At this point choosing a particular tuning is a separate question which does not involve what the temperament *is*, namely 11-limit marvel. I say 11-limit because that is what the header information claims for it, but also because of the precise tuning, which turns out to be the 11-limit minimax tuning.
Hence, Dave's scale can be *precisely* defined as the tempering by 11-limit minimax marvel of the following 5-limit scale [arranged by Monzo into tabular format, with monzos, cents, and graphics added]:
3,5-monzo ratio ~cents [ 0, 0 > 2 / 1 1200 [ 4, 2 > 2025 / 1024 1180.447431 [-3, -1 > 256 / 135 1107.821284 [ 1, 1 > 15 / 8 1088.268715 [-2, -3 > 2048 / 1125 1037.148857 [-2, 0 > 16 / 9 996.0899983 [ 2, 2 > 225 / 128 976.5374295 [-1, -2 > 128 / 75 925.4175714 [-1, 1 > 5 / 3 884.358713 [ 3, 3 > 3375 / 2048 864.8061442 [ 0, -1 > 8 / 5 813.6862861 [ 0, 2 > 25 / 16 772.6274277 [-3, -2 > 1024 / 675 721.5075697 [ 1, 0 > 3 / 2 701.9550009 [ 1, 3 > 375 / 256 660.8961425 [-2, -1 > 64 / 45 609.7762844 [ 2, 1 > 45 / 32 590.2237156 [-1, -3 > 512 / 375 539.1038575 [-1, 0 > 4 / 3 498.0449991 [ 3, 2 > 675 / 512 478.4924303 [ 0, -2 > 32 / 25 427.3725723 [ 0, 1 > 5 / 4 386.3137139 [ 4, 3 > 10125 / 8192 366.7611451 [ 1, -1 > 6 / 5 315.641287 [ 1, 2 > 75 / 64 274.5824286 [-2, -2 > 256 / 225 223.4625705 [ 2, 0 > 9 / 8 203.9100017 [ 2, 3 > 1125 / 1024 162.8511433 [-1, -1 > 16 / 15 111.7312853 [ 3, 1 > 135 / 128 92.17871646 [ 3, 4 > 16875 / 16384 51.11985806 [ 0, 0 > 1 / 1 0 |
|
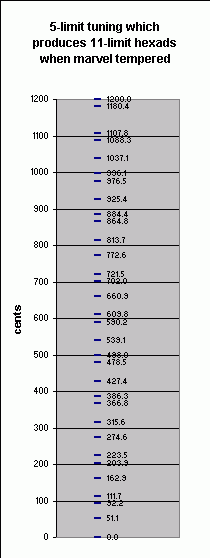
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by choosing your preferred level of financial support. Thank you.