A 13-tone 7...17-limit scale of Pat Pagano and David Beardsley

[Joe Monzo]

On the internet Tuning List, Pat Pagano presented a scale designed by he and David Beardsley, and asked for comments from other list subscribers (Message 19513, Tue Feb 27, 2001 5:24pm).

This scale uses a rational tuning, and includes the prime-factors 2, 3, 5, 7, and 17, thus characterizing it as 17-limit, albeit without making any use of the intervening prime-factors 11 and 13.

Because of these missing prime-factors, I (and others) would label it as "7...17-limit", or some other variation such as "7/17-limit".

I think it makes sense to recognize in the label that a particular tuning makes use of an inclusive set of fairly low prime-factors with one "special" prime-factor that is larger. This occurs rather often, as here.

My first response presented the prime-factor matrix which outlines the values of the exponents of all the prime-factors in the ratios of this scale (Message 19517, Tue Feb 27, 2001 6:43pm):


            2    3   5   7   17

   2/1       1   0   0   0   0
 119/64    - 6   0   0   1   1
  85/48    - 4  -1   1   0   1
  17/10    - 1   0  -1   0   1
  51/32    - 5   1   0   0   1
 119/80    - 4   0  -1   1   1
  17/12    - 2  -1   0   0   1
1377/1024  -10   4   0   0   1
  51/40    - 3   1  -1   0   1
 153/128   - 7   2   0   0   1
 425/384   - 7  -1   2   0   1
  17/16    - 4   0   0   0   1
   1/1       0   0   0   0   0

Dan Stearns then created a good ASCII lattice of these pitch relationships (Message 19528, Tue Feb 27, 2001 11:48pm):


       425/384
         /
        /
       /
    85/48
     / \
    /   \  119/64             1377/1024
   /     \  ./ `.                /
17/12---17/16----51/32-------153/128
   \    1/1X
    \  119/80
     \ /.' `.\
    17/10---51/40

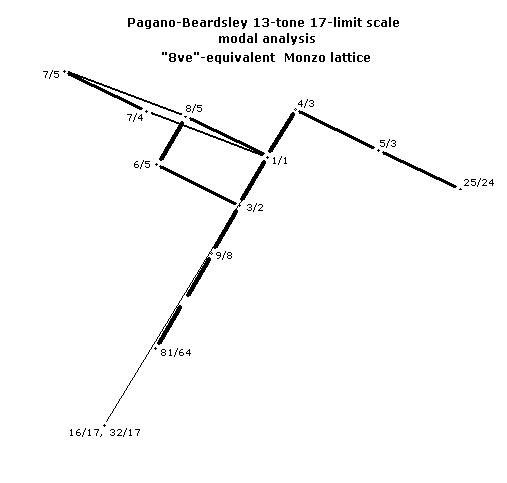
Lawrence Ball gave a correct analysis of this scale as a modal species, without actually describing it as such (Message 19537, Wed Feb 28, 2001 4:36am).

I promised to create Monzo lattices of the scale. Here they are.

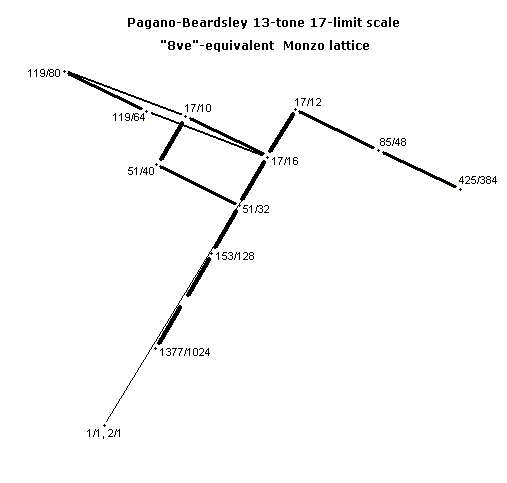
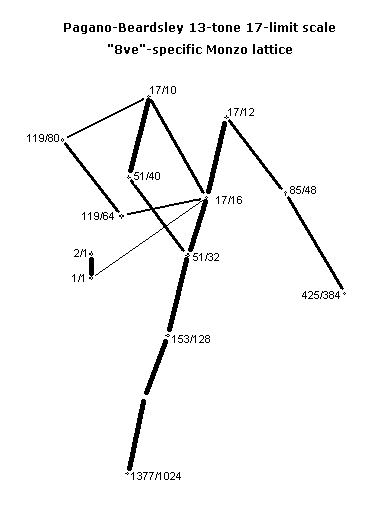
Here's the "octave"-equivalent lattice shifted in ratio-space (i.e., transposed) by a 16:17 to show the analysis of this scale as a modal species containing more familiar pitches.

Updated:

2001.3.2

Encyclopedia of Microtonal Music Theory

A 13-tone 7...17-limit scale of Pat Pagano and David Beardsley