Petr Pařízek recorded an improvisation which i really liked, in an interesting tuning.
In Yahoo Tuning Group message 74791, Thu Jan 3, 2008 7:04 am PST, Petr Pařízek wrote:
I don't know what this should be called, I don't know if someone has already mentioned this, I just know that this is not a linear temperament but it certainly is a temperament. It has two one-step interval sizes, the larger of which is 166.015 cents and the smaller one is 73.985 cents. If you stack 5L + 5S, you get an octave. But we definitely don't want to get two 5-EDO chains in this case so the pattern of LSLSLSLSLS is probably not the best choice. Instead, we can make a good 11-limit temperament if we know that:
A) 3L approximates 4/3,
B) 1L + 2S approximates 6/5,
C) 1L + 3S approximates 5/4,
D) 2L + 3S approximates 11/8.
In order to have at least one approximation of 4/3 in the scale, it is necessary to have three L sizes in a row somewhere. So, for example, we can do it like LLLSSLSLSS, which makes the scale symmetrical from the fourth degree (supposing the 1/1 is the first degree.
In Yahoo Tuning Group message 74824, Sun Jan 6, 2008 3:22 am PST, Pařízek wrote:
I'm realizing I should have told you how I made the temperament. It can be all described using four basic factors: 11/10, 12500/11979, 4000/3993, and (this one better as a PSC -- or, as you say, "monzo") "-7 6 -13 0 8" (the 0 meaning no 7s). The last two are commas that I chose to temper out. What this means is that, for example, 2/1 is then mapped to these as "5 5 2 2", 3/2 is "2 5 1 2", 5/4 is "1 3 0 1" and 11/8 is "2 3 0 1".
In Yahoo Tuning Group message 74795, Thu Jan 3, 2008 6:25 pm PST, Herman Miller wrote:
It could be described as a scale (mode?) of a regular temperament with a period of 240.0 cents and a generator of 73.985 cents. A partial generator mapping can be deduced (there isn't a very good approximation of 7/1).
[<5, 7, 11, *, 17], <0, 3, 2, *, 1]>
Or you could use your large and small steps of 166.015 cents and 73.985 cents as generators. The generator mapping then looks like this:
[<5, 7, 11, *, 17], <5, 10, 13, *, 18]>
If you do want to include the 7/1, there are a couple of 11-limit temperaments that fit this pattern. As far as I know these don't have names. The 15&50 does match George Secor's observation of this being close to 65-EDO.
[<5, 7, 11, 14, 17], <0, 3, 2, 0, 1]> 15&35, 15&50, 35&50
TOP P = 240.285642, G = 72.410116
TOP-RMS P = 240.153941, G = 73.311021[<5, 7, 11, 15, 17], <0, 3, 2, -3, 1]> 15&80, 15&95, 80&95
TOP P = 239.790292, G = 75.028284
TOP-RMS P = 239.734033, G = 74.857029[<5, 7, 11, 11, 17], <0, 3, 2, 10, 1]> 50&115
TOP P = 240.133358, G = 73.061352
TOP-RMS P = 240.025618, G = 73.076177Or you could just use it as a temperament without a 7/1 approximation.
Petr made an mp3 of an improvisation illustrating this tuning.
In Yahoo Tuning Group message 74820, Sat Jan 5, 2008 8:20 am PST, Pařízek wrote:
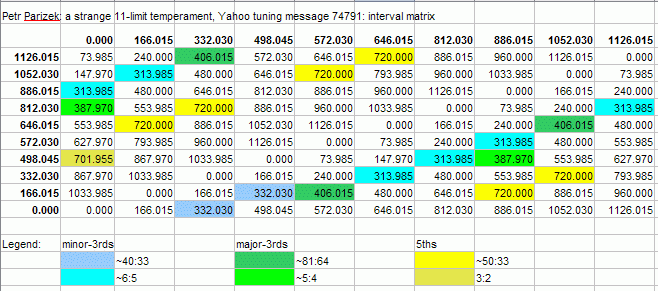
As to the tuning, Ive made a table of four columns. The first column sais which key is used for the particular scale degree. The second column (with the #in the first cell) contains the scale degree number, assuming the 1/1 is degree 0. The third column shows if the scale degree in question is away from the previous one by the larger or the smaller of the two used step sizes. And the final column contains the actual interval size from degree 0 in cents or as a ratio.F #1 L 166.015 F# not used G #2 L 332.030 G# not used A #3 L 4/3 A# #4 S 572.030 B #5 S 646.015 C #6 L 812.030 C# #7 S 886.015 D #8 L 1052.030 D# #9 S 1126.015 E #10 S 2/1
Below is an interval matrix of all the intervals in this scale. The upper pitch is listed horizontally across the top, and the lower pitch vertically along the left. Octave-equivalence is assumed. Some of the important harmonic intervals are colored, with a legend at the bottom.
I made two Tonescape files of this piece, using only a plain acoustic piano timbre (i plan to eventually "orchestrate" them):
Below is a graphic of a screenshot showing the Tonescape Lattice window for my 3,5,11-space JI version:
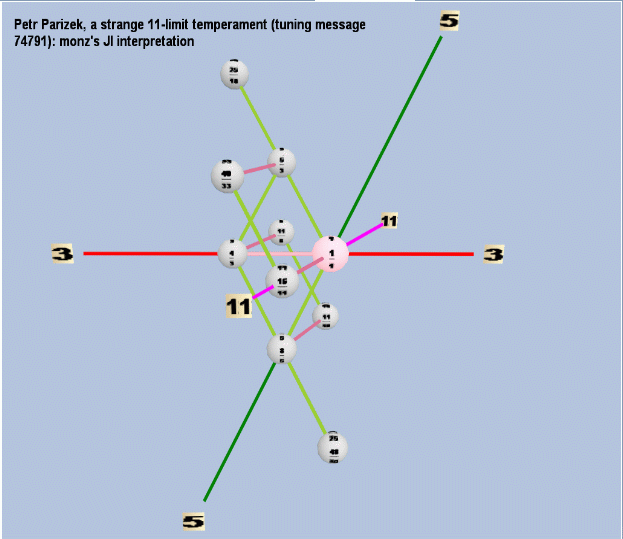
In Yahoo Tuning Group message 74821, Sat Jan 5, 2008 10:47 pm PST, monz wrote:
One version uses Petr's original temperament, and the
other is my "best fit" 3,5,11-space JI version, whose
ratios are very close to his temperament. Here are the
cents errors of Petr's temperament from my JI version:
---------- cents ------------
ratio 2,3,5,11-monzo 3,5,11-JI Petr temp error
48:25 [ 4 1, -2 0> 1129.328 1126.015 - 3.313
11:6 [-1 -1, 0 1> 1049.363 1052.030 + 2.667
5:3 [ 0 -1, 1 0> 884.359 886.015 + 1.656
8:5 [ 3 0, -1 0> 813.686 812.030 - 1.656
16:11 [ 4 0, 0 -1> 648.682 646.015 - 2.667
25:18 [-1 -2, 2 0> 568.717 572.030 + 3.313
4:3 [ 2 -1, 0 0> 498.045 498.045 0
40:33 [ 3 -1, 1 -1> 333.041 332.030 - 1.011
11:10 [-1 0, -1 1> 165.004 166.015 + 1.011
1:1 [ 0 0, 0 0> 0.000 0.000 0
It's really fun to watch the Lattice of the
JI version. The best Lattice notation to use for
that version is, naturally, "Ratio" ... but if
you want to see it with letter names, the best
letter notation Tonescape can offer so far for
this JI tuning (since it still lacks sagittal
and HEWM) is "Meantone, 1/3-comma, E".