An examination of Partch's comparison of Equal Temperaments
webpage and soundfiles © 2001 by Joe Monzo
I'm replying here to two of Graham's posts about Partch and MIRACLE.
> ----- Original Message -----
> From: graham@...
> To: tuning-math@yahoogroups.com
> Sent: Monday, June 25, 2001 2:53 AM
> Subject: [tuning-math] Re: 41 "miracle" and 43 tone scales
>
>
> One question is, how much did Partch know about Miracle when he drew up
> that original, unpublished scale? It may be stretching credulity to
> suggest he worked it all out, and then pretended it was pure JI. But the
> criteria he was using may well have matched those that are enshrined in
> Miracle. Roughly equal melodic steps will of course favour an MOS. And
> he would have been able to hear the intervals that were almost just by
> Miracle approximations. And so he could have chosen the extra notes to
> maximise these consonances.
>
> In which case, why did he change his mind later? I think it was to get
> more modulation by fifths in the 5-limit plane. With experience, he
> decided this was more important than matching the consonances.
>
> The limitations on modulation by fifths is one of the problems with
> Miracle, at least in a traditional context. Boomsliter and Creel's
> theories work very well with schismic, but not at all well with Miracle,
> temperament.
>
>br /> > ----- Original Message -----
> From: graham@...
> To: tuning-math@yahoogroups.com
> Sent: Monday, June 25, 2001 7:03 AM
> Subject: [tuning-math] Re: 41 "miracle" and 43 tone scales
>
>
> Oh, come come. If Partch was ever feeling towards Miracle he would have
> stopped doing so long before Wilson came up with his Modulus-41 ideas.
> That the scale works so well with 41 and 72 does imply Miracle. Then
> again, simply using 11-limit JI implies Miracle.
>
> It is interesting that 31, 41 and 72 don't get a mention in Genesis [of a Music].
> Deliberate avoidance of temperaments he can't dismiss so lightly? You
> decide!
Graham, you know that I also love speculation! I'm very impressed by yours here.
John Chalmers is the subscriber on this list who can really document the relationship between Secor and Partch. (Perhaps we should also post a query on another list for Kraig Grady?)
I do know, however, that their meeting ocurred quite late in Partch's life. Partch lamented that Secor's Scalatron was the instrument he had always wanted, but it came along too late to do him any good. This was probably early 1970s, possibly late 1960s.
Genesis was published in 1947 or 1949 [1] (1st ed.) and 1974 (2nd ed.), and the only substantial changes in the 2nd edition concerned Partch's new instruments. The theoretical and historical sections of the book remained virtually intact.
On the other hand, it's very much worth keeping in mind this quote from Bob Gilmore's biography of Partch (p 385):
"He had received a visit from Herman Pedtke, inventor of the Scalatron, an electronic keyboard designed to accommodate microtonal tunings -- the very instrument he had dreamed of as long ago as 1945 in Madison. Partch was fascinated by the instrument, but noted to a friend that his work had gone in a very different direction in the years since, and now involved 'far more than a microtonal scale.'"
(Thanks to Jon Szanto for providing that.)
So I'm certain beyond any doubt that Partch was not *consciously* aware of MIRACLE before the late 1960s. (note my emphasis)
But Graham's speculations are intriguing, and I'm fairly convinced by them that Partch intuitively understood the MIRACLE concept and perhaps was indeed guided in constructing his 43-tone scale by some of the additional "senses" in which the 14 new (and original 29) pitches could be taken in MIRACLE.
Daniel Wolf, who has had the opportunity to study Partch's
scores in *much* greater depth than I have, has remarked on how
Partch did not always construct his harmonies according to the
lowest-odd-integer hexadic theory presented in Genesis.
So perhaps some of these "nonstandard" usages do conform
to MIRACLE-like approximations.
Partch's 14 additional pitches are, as Graham correctly states,
primarily an expansion of the Tonality Diamond in the prime-factor-3
dimension, which Graham notes is not a feature of MIRACLE.
I've noted before how I thought it was a paradox that for all
his vitriolic abrogation of Pythagoreanism, Partch took exactly
this route in expanding his pitch gamut. It seems that he valued
something about traditional music-theory after all ;-) , and that
"something" is, again as Graham points out, modulation or
root-movement by 3:2s.
About the equal temperaments discussed in _Genesis_:
First of all, I should say that I was simply writing from memory
before. Now I have the book in front of me, and there are indeed
some ETs that I left out. I'll correct that omission abundantly
now.
Partch (1974, p 417) does make this interesting general observation:
He opens his chapter on equal-temperaments with a long and
scathing diatribe against 12-EDO,
which, by this point in the book, should not surprise the reader.
Then he discusses the 'First Result of Expansion - "Quartertones"'.
Upon mentioning Carillo, Partch also thus mentions 48- and 96-EDO.
(not using that actual term, of course)
But he actually does go into a little detail about 24-EDO, and
he's even generous enough about its potential to say that
'As a temporary expedient, as an immediately feasible method
of creating new musical resources, "quartertones" are valuable'.
He mentions Haba [which should be spelled Hába], Hans Barth, and
Mildred
Couper and their use of dual regular keyboards, and Meyer
and Möllendorf
and their new keyboards.
Then Partch breifly discusses Busoni and 36-EDO, which he characterizes
as "another Polypythagoreanism in tempered expression".
In the middle of this text, on p 430, is Partch's comparative table
of tunings. I will come back to say more about this table after
describing the rest of the text.
Next comes the discussion of Yasser's 19-EDO, then finally 53-EDO.
About Yasser's proposal, Partch emphasizes that its goal is
not the betterment of intonation, but simply an expansion of
scalar resources. He notes the improved approximations to
5- and 7-limit ratios, and also that "The ratios of 7 are somewhat
better also, but still with a maximum falsity of 21.4 cents
(33.1 cents in twelve-tone temperament). The ratios of 11 are
not represented at all".
Note that Partch is rounding his cent-values to the nearest 1/10th
without saying so. Actually, 19-EDO's closest approximations
to the 11-limit ratios are all between +/- ~17.1 and ~31.5 cents,
and all significantly better than 12-EDO's (but not good enough
for Partch).
(These tables and graphs show the closest approximations of
19-EDO to 11-limit ratios. The graph on the left plots the
error of 19-EDO from JI, and the graph on the right compares
the interval sizes of the two tunings.)
Partch had mentioned in "Chapter 15: A Thumbnail Sketch of the
History of Intonation" that King Fang (in China) and Mersenne,
Kircher, and Mercator (in Europe) all proposed 53-EDO.
In the middle of this discussion is a digression
"On the Matter of Hearing a 2-Cents Falsity".
Partch notes that 53-EDO is indeed extremely close to 3- and
5-limit JI, but does not consider it suitable for his own use
as it offers little improvement in approximating the 7- and
11-limit ratios he wanted to use.
Finally he examines the 53-EDO keyboard proposals of Nicolaus Ramarinus
(1640) [2], Bosanquet (no date given by Partch, c. 1875?), and
Jas. Paul White (1883) [3].
And that wraps up Partch's "Chapter 17: Equal Temperaments".
Now, back to that comparative table...
Partch's table on p 430 compares his Monophonic 43-tone scale with,
in order:
> Fundamentally, equal temperaments are based upon and deduced
> from Pythagorean "cycles," in whole or part.

First, I should note that there are obviously tunings here (the second, third, and fourth) which are not ETs. Partch had already discussed these in his "Chapter 16: Polypythagoreanism".
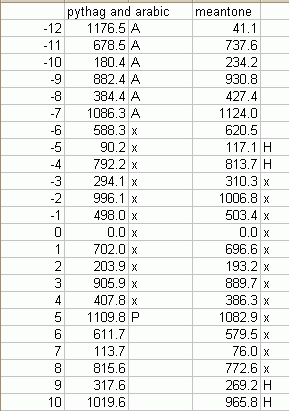
(In this table, the first column gives the Pythagorean tunings as a "cycle of 5ths"; "x" marks pitches used in both tunings given by Partch, "P" is used only in the 12-tone Pythagorean, and "A" marks those in the Arabic scale. The second column gives 1/4-comma meantone as a "cycle of 5ths", with "x" marking the "usual" 12-tone cycle and "H" designating the four extra pitches used by Handel.)
But - SURPRISE! - there's 31-EDO in the table, but WITH NO MENTION WHATSOEVER IN THE TEXT!!
And I checked all the other chapters in Genesis... there's no mention at all of Huyghens, Fokker, or anything else concerning 31-EDO.
Now THAT'S interesting! ... And I never noticed it before, having been duped by 31-EDO's appearance in that table into thinking that Partch said something about it somewhere.
So Graham is right that, except for this inconspicuous little tabulation, Partch does not mention 31-, 41- or 72-EDO. Good detective work, Graham!!!
NOTES
[1] I asked before (on the main list) about the actual publication date. I don't remember now what the outcome was, but I've seen it listed in catalogs under both dates. The original Preface is dated April 1947, but the copyright date is 1949.
[2] About Ramarinus, Partch says:
> the "tone" (9/8) was divided into nine "commas",
> according to Hawkins [_History of the Science and
> Practice of Music, vol 1, p 396]. The fifty-third part
> of 2/1 is approximately the width of the "comma" of
> Didymus, 81/80 (21.5 cents; see table above), and since
> six 9/8's are larger than a 2/1 by approximately this
> interval (the "comma" of Pythagoras, 23.5 cents), this
> procedure would result in a fifty-three-tone scale.
The 9-commas-per-tone temperament works out to either 55-EDO, which is a meantone, or 53-EDO, which is quasi-just, depending on which of the two types of semitone is larger, the diatonic or the chromatic.
If the chromatic semitone is the larger of the two, then the diatonic scale (5 L + 2 s) has 9 commas per "L" and 4 commas per "s", and results in (5 * 9) + (2 * 4) = 53-EDO.
If the diatonic semitone is the larger of the two, then the diatonic scale has 9 commas per "L" and 5 commas per "s", and results in (5 * 9) + (2 * 5) = 55-EDO.
This choice might reflect Partch's own bias -- I'd bet that Ramarinus most likely meant something more like 55-EDO. But I haven't been able to confirm this supposition: I've done several internet searches and have found nothing at all about Ramarinus.
[3] Paul (or anyone else in Boston): It still says in the 1974 edition of Genesis that White's harmonium was housed in a practice room at New England Conservatory, and that Partch examined it in 1943. I've found page references in Genesis that should have been renumbered from the 1st edition and weren't, so perhaps this is a story that also should have been updated. Please... go take a look and let us know!
Updates:
-
2001.6.25
2002.1.22
