© 2000 by Joe Monzo
American composer Harry Partch (1901-1974) based all of his mature musical compositions on a musical scale tuned in just intonation and based on the 11-limit tonality diamond, played on instruments he designed and built himself to be played in that tuning. The number of notes varied for a time from about 29 to 55, until he finally settled on a scale of 43 tones to the octave (his identity interval, which Partch always referred to by its frequency ratio 2/1).
Partch's tuning is often called "extended just intonation", because traditional just intonation used ratios with only the prime-factors 2, 3, and 5, whereas Partch added 7 and 11 to these.
Below is a tabulation of the scale, with the 2,3,5,7,11-monzo, ratio, and approximate cents value, for each pitch. Next to the table is a graph showing the pitch-height of the ratios.
2,3,5,7,11-monzo ratio ~cents [ 1 0, 0 0 0 > 2 / 1 1200.0 [ 5 -4, 1 0 0 > 160 / 81 1178.49371 [ 6 -1, 0 0 -1 > 64 / 33 1146.727057 [ 3 -1, 1 -1 0 > 40 / 21 1115.532807 [-3 1, 1 0 0 > 15 / 8 1088.268715 [-1 -1, 0 0 1 > 11 / 6 1049.362941 [ 2 0, 1 0 -1 > 20 / 11 1034.995772 [ 0 2, -1 0 0 > 9 / 5 1017.596288 [ 4 -2, 0 0 0 > 16 / 9 996.0899983 [-2 0, 0 1 0 > 7 / 4 968.8259065 [ 2 1, 0 -1 0 > 12 / 7 933.1290944 [-4 3, 0 0 0 > 27 / 16 905.8650026 [ 0 -1, 1 0 0 > 5 / 3 884.358713 [ 1 2, 0 0 -1 > 18 / 11 852.5920594 [ 3 0, -1 0 0 > 8 / 5 813.6862861 [ 0 0, 0 -1 1 > 11 / 7 782.4920359 [ 1 -2, 0 1 0 > 14 / 9 764.9159047 [ 5 -1, 0 -1 0 > 32 / 21 729.2190927 [-1 1, 0 0 0 > 3 / 2 701.9550009 [ 3 -3, 1 0 0 > 40 / 27 680.4487113 [ 4 0, 0 0 -1 > 16 / 11 648.6820576 [ 1 0, 1 -1 0 > 10 / 7 617.4878074 [ 0 0, -1 1 0 > 7 / 5 582.5121926 [-3 0, 0 0 1 > 11 / 8 551.3179424 [-2 3, -1 0 0 > 27 / 20 519.5512887 [ 2 -1, 0 0 0 > 4 / 3 498.0449991 [-4 1, 0 1 0 > 21 / 16 470.7809073 [ 0 2, 0 -1 0 > 9 / 7 435.0840953 [ 1 0, 0 1 -1 > 14 / 11 417.5079641 [-2 0, 1 0 0 > 5 / 4 386.3137139 [ 0 -2, 0 0 1 > 11 / 9 347.4079406 [ 1 1, -1 0 0 > 6 / 5 315.641287 [ 5 -3, 0 0 0 > 32 / 27 294.1349974 [-1 -1, 0 1 0 > 7 / 6 266.8709056 [ 3 0, 0 -1 0 > 8 / 7 231.1740935 [-3 2, 0 0 0 > 9 / 8 203.9100017 [ 1 -2, 1 0 0 > 10 / 9 182.4037121 [-1 0, -1 0 1 > 11 / 10 165.0042285 [ 2 1, 0 0 -1 > 12 / 11 150.6370585 [ 4 -1, -1 0 0 > 16 / 15 111.7312853 [-2 1, -1 1 0 > 21 / 20 84.46719347 [-5 1, 0 0 1 > 33 / 32 53.27294323 [-4 4, -1 0 0 > 81 / 80 21.5062896 [ 0 0, 0 0 0 > 1 / 1 0.0 |
|
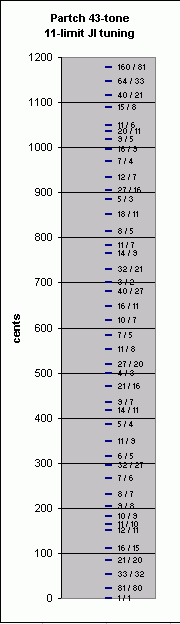
Below are two views of a Tonescape lattice diagram of Partch's 43-tone just intonation scale; it is a 3-dimensional projection of a 4-dimensional lattice, with axes representing prime-factors 3, 5, 7, 11.
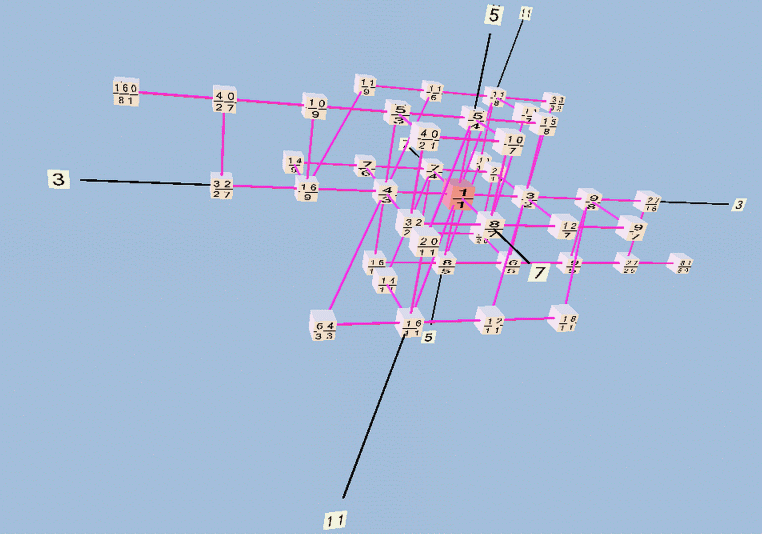
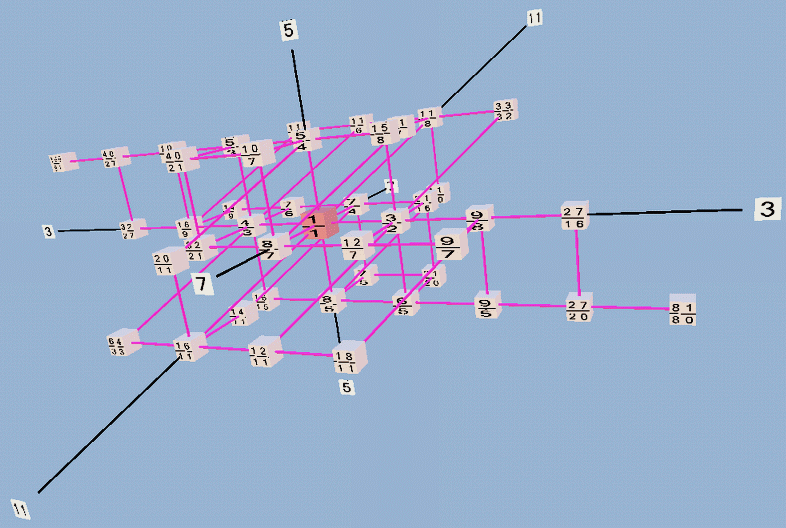
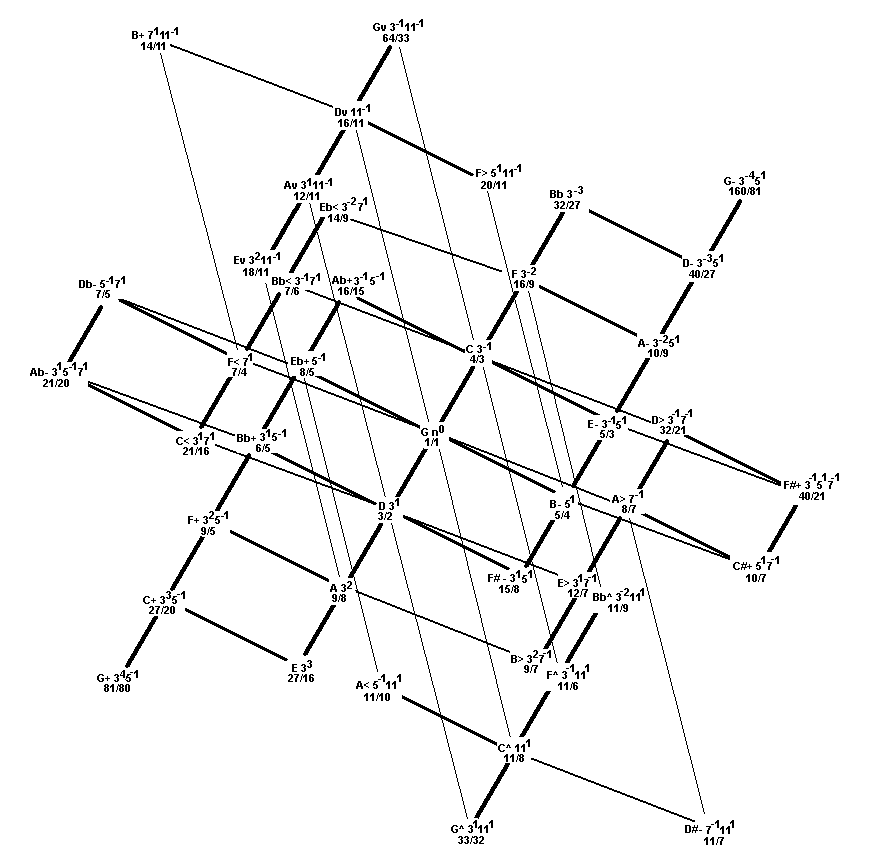
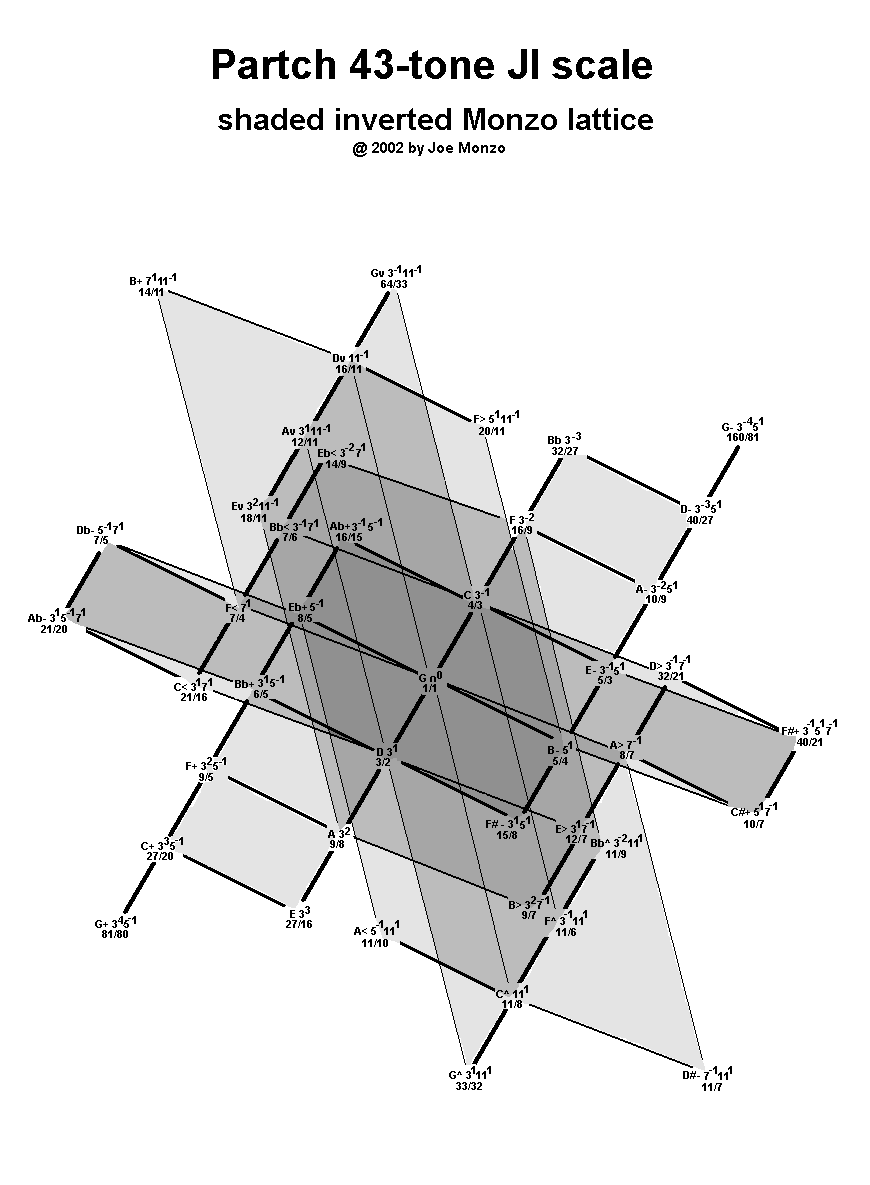
Below is an inverted Monzo lattice of Harry Partch's 43-tone JI scale. Pitches are notated in three formats:
First, the plain lattice:
Next, a shaded version which portrays more readily the 4-dimensionality of the lattice by coloring the planes of the lattice -- each of which incorporates two of the four prime-factors 3, 5, 7, and 11 -- as tho they were panes of transparent tinted glass:
The graph below shows the standard deviation of all EDOs from 43 to 1200. With the desideratum to have the best combination of lowest standard deviation and lowest cardinality, the three clear winners are 72-, 120-, 152-, 183-, 224-, and 270-edo. 270edo even gives a better approximation of Partch's scale than 1200edo (the measurement of cents)!
