Below is a list of pitches in 37-edo, arranged in descending order of pitch, showing cents, genes, and tinas.
37-edo deg ~cents exact cents genes exact genes tinas exact tinas 37 1200.000 1200 + 0 / 37 311 311 + 0 / 37 8539 8539 + 0 / 37 36 1167.568 1167 + 21 / 37 303 302 + 22 / 37 8308 8308 + 8 / 37 35 1135.135 1135 + 5 / 37 294 294 + 7 / 37 8077 8077 + 16 / 37 34 1102.703 1102 + 26 / 37 286 285 + 29 / 37 7847 7846 + 24 / 37 33 1070.270 1070 + 10 / 37 277 277 + 14 / 37 7616 7615 + 32 / 37 32 1037.838 1037 + 31 / 37 269 268 + 36 / 37 7385 7385 + 3 / 37 31 1005.405 1005 + 15 / 37 261 260 + 21 / 37 7154 7154 + 11 / 37 30 972.973 972 + 36 / 37 252 252 + 6 / 37 6924 6923 + 19 / 37 29 940.541 940 + 20 / 37 244 243 + 28 / 37 6693 6692 + 27 / 37 28 908.108 908 + 4 / 37 235 235 + 13 / 37 6462 6461 + 35 / 37 27 875.676 875 + 25 / 37 227 226 + 35 / 37 6231 6231 + 6 / 37 26 843.243 843 + 9 / 37 219 218 + 20 / 37 6000 6000 + 14 / 37 25 810.811 810 + 30 / 37 210 210 + 5 / 37 5770 5769 + 22 / 37 24 778.378 778 + 14 / 37 202 201 + 27 / 37 5539 5538 + 30 / 37 23 745.946 745 + 35 / 37 193 193 + 12 / 37 5308 5308 + 1 / 37 22 713.514 713 + 19 / 37 185 184 + 34 / 37 5077 5077 + 9 / 37 21 681.081 681 + 3 / 37 177 176 + 19 / 37 4846 4846 + 17 / 37 20 648.649 648 + 24 / 37 168 168 + 4 / 37 4616 4615 + 25 / 37 19 616.216 616 + 8 / 37 160 159 + 26 / 37 4385 4384 + 33 / 37 18 583.784 583 + 29 / 37 151 151 + 11 / 37 4154 4154 + 4 / 37 17 551.351 551 + 13 / 37 143 142 + 33 / 37 3923 3923 + 12 / 37 16 518.919 518 + 34 / 37 134 134 + 18 / 37 3693 3692 + 20 / 37 15 486.486 486 + 18 / 37 126 126 + 3 / 37 3462 3461 + 28 / 37 14 454.054 454 + 2 / 37 118 117 + 25 / 37 3231 3230 + 36 / 37 13 421.622 421 + 23 / 37 109 109 + 10 / 37 3000 3000 + 7 / 37 12 389.189 389 + 7 / 37 101 100 + 32 / 37 2769 2769 + 15 / 37 11 356.757 356 + 28 / 37 92 92 + 17 / 37 2539 2538 + 23 / 37 10 324.324 324 + 12 / 37 84 84 + 2 / 37 2308 2307 + 31 / 37 9 291.892 291 + 33 / 37 76 75 + 24 / 37 2077 2077 + 2 / 37 8 259.459 259 + 17 / 37 67 67 + 9 / 37 1846 1846 + 10 / 37 7 227.027 227 + 1 / 37 59 58 + 31 / 37 1615 1615 + 18 / 37 6 194.595 194 + 22 / 37 50 50 + 16 / 37 1385 1384 + 26 / 37 5 162.162 162 + 6 / 37 42 42 + 1 / 37 1154 1153 + 34 / 37 4 129.730 129 + 27 / 37 34 33 + 23 / 37 923 923 + 5 / 37 3 97.297 97 + 11 / 37 25 25 + 8 / 37 692 692 + 13 / 37 2 64.865 64 + 32 / 37 17 16 + 30 / 37 462 461 + 21 / 37 1 32.432 32 + 16 / 37 8 8 + 15 / 37 231 230 + 29 / 37 0 0.000 0 + 0 / 37 0 0 + 0 / 37 0 0 + 0 / 37
37-edo is the lowest cardinality of equal-temperament which provides good approximations of JI pitches thru the 13-limit, with the caveat that the approximation of 3 is only mediocre.
On 5 April 2012, Joe Monzo posted an inquiry on the Yahoo! tuning-math group stating that the Tenny-Minkowski reduced lattice basis for a 37-tone Fokker periodicity-block did not produce mappings of the unit generators for prime-factors 7, 11, and 13, and that did include pitches which go too far along the 3-axis, considering that 37-edo's approximation of 3 is not very good. Monzo then asked if anyone could provide a set of unison-vectors which would meet his desired conditions, and Gene Ward Smith responded a few times, the last response [Yahoo! tuning-math group, message 20560] giving a complete Scala file with the appropriate block.
! monzoblock37.scl ! Symmetrical 13-limit Fokker block containing all of the primes as scale degrees ! Commas: 512/507, 121/120, 91/90, 385/384, 64/63; all generators -18 to 18 37 ! 1024/1001 33/32 16/15 13/12 12/11 44/39 8/7 7/6 13/11 77/64 16/13 5/4 33/26 13/10 4/3 192/143 11/8 128/91 91/64 16/11 143/96 3/2 20/13 52/33 8/5 13/8 128/77 22/13 12/7 7/4 39/22 11/6 24/13 15/8 64/33 1001/512 2/1
Below is a Tonescape® Lattice illustrating this periodicity-block, using triangular geometry in 3,5,7,11,13-prime-space. This is rendered as a 2-dimensional representation of a 3-dimensional shadow of a 5-dimensional structure. Prime-factor 2 is not shown, since it is being employed as the identity-interval.
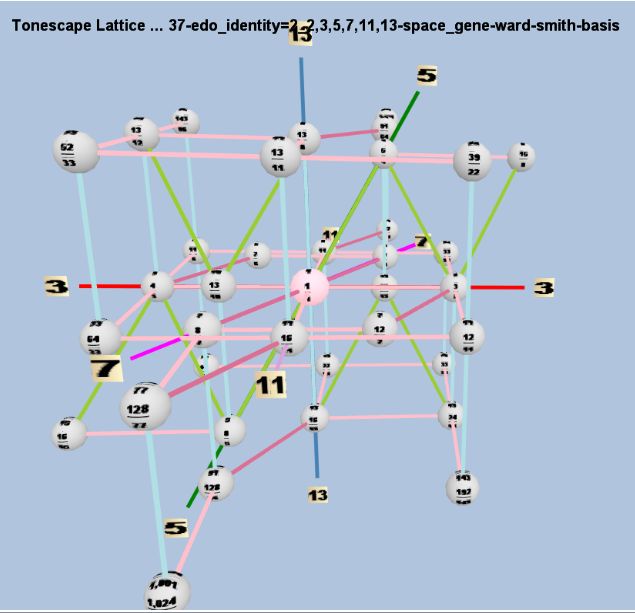
Download the Tonescape .tuning file of 37-edo using this periodicity-block for its Lattice structure.
Below is an analysis of the mappings and pitches in this periodicity-block:
unison-vectors:
ratio 2, 3, 5, 7, 11, 13 - monzo
512:507 = [ 9, -1, 0, 0, 0, -2>
121:120 = [-3, -1, -1, 0, 2, 0>
91:90 = [-1, -2, -1, 1, 0, 1>
385:384 = [-7, -1, 1, 1, 1, 0>
64:63 = [ 6, -2, 0, -1, 0, 0>
floating-point mappings:
prime edo-steps step-error edo-map
2 = 37.000000 +0.00 --> 37
3 = 58.643613 +0.36 --> 59
5 = 85.911340 +0.09 --> 86
7 = 103.872132 +0.13 --> 104
11 = 127.998970 +0.00 --> 128
13 = 136.916270 +0.08 --> 137
integer (i.e., true) mappings, compared with cents-value of actual prime
map 2 --> 37 = 1200.000000 cents <-- 1200.000000 + 0.0 cents
map 3 --> 59 = 1913.513514 cents <-- 1901.955001 +11.6 cents
map 5 --> 86 = 2789.189189 cents <-- 2786.313714 + 2.9 cents
map 7 --> 104 = 3372.972973 cents <-- 3368.825906 + 4.1 cents
map 11 --> 128 = 4151.351351 cents <-- 4151.317942 + 0.0 cents
map 13 --> 137 = 4443.243243 cents <-- 4440.527662 + 2.7 cents
--------------
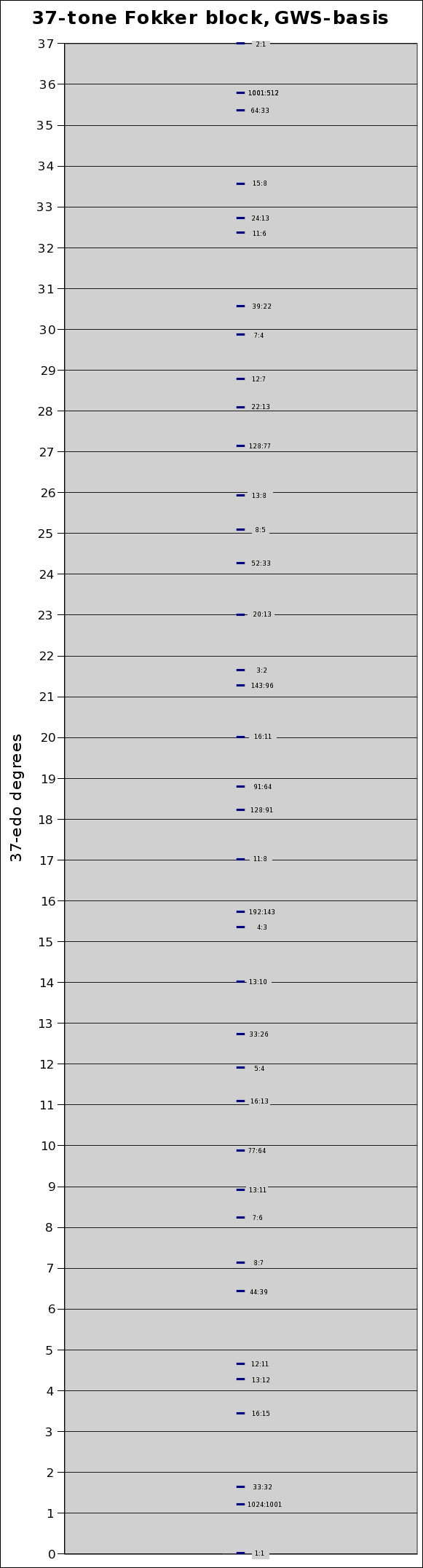
37-tone Fokker periodicity-block, using gws-basis (Gene Ward Smith):
ratio --> 37 -edo mapping:
ratio cents error edo cents name
2:1 = 1200.0 + 0.0 --> 37/37 = 1200.0 (octave)
1001:512 = 1160.7 + 6.9 --> 36/37 = 1167.6 ()
64:33 = 1146.7 -11.6 --> 35/37 = 1135.1 ()
15:8 = 1088.3 +14.4 --> 34/37 = 1102.7 (just major-7th)
24:13 = 1061.4 + 8.8 --> 33/37 = 1070.3 ()
11:6 = 1049.4 -11.5 --> 32/37 = 1037.8 ()
39:22 = 991.2 +14.2 --> 31/37 = 1005.4 ()
7:4 = 968.8 + 4.1 --> 30/37 = 973.0 (harmonic-7th)
12:7 = 933.1 + 7.4 --> 29/37 = 940.5 ()
22:13 = 910.8 - 2.7 --> 28/37 = 908.1 ()
128:77 = 879.9 - 4.2 --> 27/37 = 875.7 ()
13:8 = 840.5 + 2.7 --> 26/37 = 843.2 (harmonic-13th)
8:5 = 813.7 - 2.9 --> 25/37 = 810.8 (just minor-6th)
52:33 = 787.3 - 8.9 --> 24/37 = 778.4 ()
20:13 = 745.8 + 0.2 --> 23/37 = 745.9 ()
3:2 = 702.0 +11.6 --> 22/37 = 713.5 (perfect-5th)
143:96 = 689.9 - 8.8 --> 21/37 = 681.1 ()
16:11 = 648.7 - 0.0 --> 20/37 = 648.6 (subharmonic-11th)
91:64 = 609.4 + 6.9 --> 19/37 = 616.2 ()
128:91 = 590.6 - 6.9 --> 18/37 = 583.8 ()
11:8 = 551.3 + 0.0 --> 17/37 = 551.4 (harmonic-11th)
192:143 = 510.1 + 8.8 --> 16/37 = 518.9 ()
4:3 = 498.0 -11.6 --> 15/37 = 486.5 (perfect-4th)
13:10 = 454.2 - 0.2 --> 14/37 = 454.1 ()
33:26 = 412.7 + 8.9 --> 13/37 = 421.6 ()
5:4 = 386.3 + 2.9 --> 12/37 = 389.2 (just major-3rd)
16:13 = 359.5 - 2.7 --> 11/37 = 356.8 (subharmonic-13th)
77:64 = 320.1 + 4.2 --> 10/37 = 324.3 ()
13:11 = 289.2 + 2.7 --> 9/37 = 291.9 ()
7:6 = 266.9 - 7.4 --> 8/37 = 259.5 (subminor-3rd)
8:7 = 231.2 - 4.1 --> 7/37 = 227.0 (subharmonic-7th, septimal large-2nd)
44:39 = 208.8 -14.2 --> 6/37 = 194.6 ()
12:11 = 150.6 +11.5 --> 5/37 = 162.2 ()
13:12 = 138.6 - 8.8 --> 4/37 = 129.7 ()
16:15 = 111.7 -14.4 --> 3/37 = 97.3 (just minor-2nd)
33:32 = 53.3 +11.6 --> 2/37 = 64.9 ()
1024:1001 = 39.3 - 6.9 --> 1/37 = 32.4 ()
1:1 = 0.0 + 0.0 --> 0/37 = 0.0 (prime)
Below is a pitch-height graph, showing the 37 tones of the Fokker periodicity-block against a grid for the y-axis which represents the degrees of 37-edo:
Below is a table showing how some of the most common just-intonation ratios in the 41-limit are mapped to 37-edo, using the closest-fit mappings:
37 -edo floating-point mappings:
prime edo-steps step-error edo-map
2 = 37.000000 +0.00 --> 37
3 = 58.643613 +0.36 --> 59
5 = 85.911340 +0.09 --> 86
7 = 103.872132 +0.13 --> 104
11 = 127.998970 +0.00 --> 128
13 = 136.916270 +0.08 --> 137
17 = 151.236125 -0.24 --> 151
19 = 157.173318 -0.17 --> 157
23 = 167.371792 -0.37 --> 167
29 = 179.745297 +0.25 --> 180
31 = 183.305263 -0.31 --> 183
37 = 192.749775 +0.25 --> 193
41 = 198.229424 -0.23 --> 198
43 = 200.771796 +0.23 --> 201
integer (i.e., true) mappings, compared with cents-value of actual prime
map 2 --> 37 = 1200.000000 cents <-- 1200.000000 + 0.0 cents
map 3 --> 59 = 1913.513514 cents <-- 1901.955001 +11.6 cents
map 5 --> 86 = 2789.189189 cents <-- 2786.313714 + 2.9 cents
map 7 --> 104 = 3372.972973 cents <-- 3368.825906 + 4.1 cents
map 11 --> 128 = 4151.351351 cents <-- 4151.317942 + 0.0 cents
map 13 --> 137 = 4443.243243 cents <-- 4440.527662 + 2.7 cents
map 17 --> 151 = 4897.297297 cents <-- 4904.955410 - 7.7 cents
map 19 --> 157 = 5091.891892 cents <-- 5097.513016 - 5.6 cents
map 23 --> 167 = 5416.216216 cents <-- 5428.274347 -12.1 cents
map 29 --> 180 = 5837.837838 cents <-- 5829.577194 + 8.3 cents
map 31 --> 183 = 5935.135135 cents <-- 5945.035572 - 9.9 cents
map 37 --> 193 = 6259.459459 cents <-- 6251.344039 + 8.1 cents
map 41 --> 198 = 6421.621622 cents <-- 6429.062406 - 7.4 cents
map 43 --> 201 = 6518.918919 cents <-- 6511.517706 + 7.4 cents
--------------
examples:
ratio --> 37 -edo mapping:
ratio cents error edo cents name
2:1 = 1200.0 + 0.0 --> 37/37 = 1200.0 (octave)
243:128 = 1109.8 + 57.8 --> 36/37 = 1167.6 (pythagorean major-7th)
31:16 = 1145.0 - 9.9 --> 35/37 = 1135.1 (31st harmonic)
21:11 = 1119.5 + 15.7 --> 35/37 = 1135.1 (undecimal diminished-8ve)
15:8 = 1088.3 + 14.4 --> 34/37 = 1102.7 (15th harmonic, just major-7th, 5*3)
13:7 = 1071.7 - 1.4 --> 33/37 = 1070.3 (tridecimal superminor-7th)
24:13 = 1061.4 + 8.8 --> 33/37 = 1070.3 (tridecimal major-7th)
11:6 = 1049.4 - 11.5 --> 32/37 = 1037.8 (undecimal submajor[neutral]-7th)
20:11 = 1035.0 + 2.8 --> 32/37 = 1037.8 (undecimal superminor[neutral]-7th)
29:16 = 1029.6 + 8.3 --> 32/37 = 1037.8 (29th harmonic)
9:5 = 1017.6 + 20.2 --> 32/37 = 1037.8 (just minor-7th)
4096:2187 = 1086.3 - 80.9 --> 31/37 = 1005.4 (pythagorean diminished-8ve)
16:9 = 996.1 - 23.1 --> 30/37 = 973.0 (pythagorean minor-7th)
7:4 = 968.8 + 4.1 --> 30/37 = 973.0 (7th harmonic, septimal subminor-7th)
19:11 = 946.2 - 5.7 --> 29/37 = 940.5 (nondecimal supermajor-6th)
12:7 = 933.1 + 7.4 --> 29/37 = 940.5 (septimal supermajor-6th)
27:16 = 905.9 + 34.7 --> 29/37 = 940.5 (27th harmonic, pythagorean major-6th)
22:13 = 910.8 - 2.7 --> 28/37 = 908.1 (tridecimal augmented-6th)
6561:4096 = 815.6 + 92.5 --> 28/37 = 908.1 (pythagorean augmented-5th)
5:3 = 884.4 - 8.7 --> 27/37 = 875.7 (just major-6th)
18:11 = 852.6 + 23.1 --> 27/37 = 875.7 (undecimal superminor[neutral]-6th)
13:8 = 840.5 + 2.7 --> 26/37 = 843.2 (13th harmonic)
21:13 = 830.3 + 13.0 --> 26/37 = 843.2 (tridecimal ?)
8:5 = 813.7 - 2.9 --> 25/37 = 810.8 (just minor-6th)
11:7 = 782.5 - 4.1 --> 24/37 = 778.4 (undecimal augmented-5th)
25:16 = 772.6 + 5.8 --> 24/37 = 778.4 (25th harmonic, just augmented-5th)
128:81 = 792.2 - 46.2 --> 23/37 = 745.9 (pythagorean minor-6th)
14:9 = 764.9 - 19.0 --> 23/37 = 745.9 (septimal subminor-6th)
17:11 = 753.6 - 7.7 --> 23/37 = 745.9 (septendecimal diminished-6th)
20:13 = 745.8 + 0.2 --> 23/37 = 745.9 (tridecimal augmented-5th)
3:2 = 702.0 + 11.6 --> 22/37 = 713.5 (perfect-5th)
729:512 = 611.7 + 69.4 --> 21/37 = 681.1 (pythagorean augmented-4th)
19:13 = 657.0 - 8.3 --> 20/37 = 648.6 (nondecimal doubly-augmented-4th)
16:11 = 648.7 - 0.0 --> 20/37 = 648.6 (11th subharmonic, undecimal diminished-4th)
13:9 = 636.6 - 20.4 --> 19/37 = 616.2 (tridecimal diminished-5th)
23:16 = 628.3 - 12.1 --> 19/37 = 616.2 (23rd harmonic)
10:7 = 617.5 - 1.3 --> 19/37 = 616.2 (septimal large-tritone)
45:32 = 590.2 + 26.0 --> 19/37 = 616.2 (just augmented-4th)
64:45 = 609.8 - 26.0 --> 18/37 = 583.8 (just diminished-5th)
7:5 = 582.5 + 1.3 --> 18/37 = 583.8 (septimal small-tritone)
18:13 = 563.4 + 20.4 --> 18/37 = 583.8 (tridecimal augmented-4th)
11:8 = 551.3 + 0.0 --> 17/37 = 551.4 (11th harmonic, undecimal sub-augmented-4th)
15:11 = 537.0 + 14.4 --> 17/37 = 551.4 (undecimal large-4th)
1024:729 = 588.3 - 69.4 --> 16/37 = 518.9 (pythagorean diminished-5th)
4:3 = 498.0 - 11.6 --> 15/37 = 486.5 (perfect-4th)
21:16 = 470.8 + 15.7 --> 15/37 = 486.5 (21st harmonic, septimal-4th, 7*3)
17:13 = 464.4 - 10.4 --> 14/37 = 454.1 (septendecimal 4th)
13:10 = 454.2 - 0.2 --> 14/37 = 454.1 (tridecimal diminished-4th)
9:7 = 435.1 + 19.0 --> 14/37 = 454.1 (septimal supermajor-3rd)
81:64 = 407.8 + 46.2 --> 14/37 = 454.1 (pythagorean major-3rd)
41:32 = 429.1 - 7.4 --> 13/37 = 421.6 (41st harmonic)
14:11 = 417.5 + 4.1 --> 13/37 = 421.6 (undecimal diminished-4th)
19683:16384 = 317.6 +104.0 --> 13/37 = 421.6 (pythagorean augmented-2nd)
5:4 = 386.3 + 2.9 --> 12/37 = 389.2 (5th harmonic, just major-3rd)
16:13 = 359.5 - 2.7 --> 11/37 = 356.8 (tridecimal major[neutral]-3rd)
39:32 = 342.5 + 14.3 --> 11/37 = 356.8 (39th harmonic, 13*3)
11:9 = 347.4 - 23.1 --> 10/37 = 324.3 (undecimal neutral-3rd)
6:5 = 315.6 + 8.7 --> 10/37 = 324.3 (just minor-3rd)
8192:6561 = 384.4 - 92.5 --> 9/37 = 291.9 (pythagorean diminished-4th)
19:16 = 297.5 - 5.6 --> 9/37 = 291.9 (19th harmonic)
13:11 = 289.2 + 2.7 --> 9/37 = 291.9 (tridecimal diminished-3rd)
75:64 = 274.6 + 17.3 --> 9/37 = 291.9 (just augmented-2nd)
32:27 = 294.1 - 34.7 --> 8/37 = 259.5 (pythagorean minor-3rd)
7:6 = 266.9 - 7.4 --> 8/37 = 259.5 (septimal subminor-3rd)
37:32 = 251.3 + 8.1 --> 8/37 = 259.5 (37th harmonic)
15:13 = 247.7 + 11.7 --> 8/37 = 259.5 (tridecimal augmented[neutral]-2nd)
8:7 = 231.2 - 4.1 --> 7/37 = 227.0 (septimal tone, supermajor-2nd)
9:8 = 203.9 + 23.1 --> 7/37 = 227.0 (pythagorean major-2nd/tone)
2187:2048 = 113.7 + 80.9 --> 6/37 = 194.6 (pythagorean augmented-prime/apotome)
10:9 = 182.4 - 20.2 --> 5/37 = 162.2 (just minor-tone)
11:10 = 165.0 - 2.8 --> 5/37 = 162.2 (undecimal small-tone/submajor-2nd)
35:32 = 155.1 + 7.0 --> 5/37 = 162.2 (35th harmonic, 7*5)
12:11 = 150.6 + 11.5 --> 5/37 = 162.2 (undecimal large-semitone)
13:12 = 138.6 - 8.8 --> 4/37 = 129.7 (tridecimal minor-2nd)
14:13 = 128.3 + 1.4 --> 4/37 = 129.7 (tridecimal major-2nd)
15:14 = 119.4 + 10.3 --> 4/37 = 129.7 (septimal chromatic-semitone)
16:15 = 111.7 - 14.4 --> 3/37 = 97.3 (just diatonic-semitone)
17:16 = 105.0 - 7.7 --> 3/37 = 97.3 (17th harmonic, septendecimal semitone)
25:24 = 70.7 - 5.8 --> 2/37 = 64.9 (just chromatic-semitone)
33:32 = 53.3 + 11.6 --> 2/37 = 64.9 (33rd harmonic, 11*3)
256:243 = 90.2 - 57.8 --> 1/37 = 32.4 (pythagorean minor-2nd/limma)
1:1 = 0.0 + 0.0 --> 0/37 = 0.0 (prime)
some commas:
3-limit
ratio cents error edo cents name
531441:524288 = 23.5 +138.7 --> 5/37 = 162.2 (pythagorean-comma)
5-limit
ratio cents error edo cents name
648:625 = 62.6 + 34.7 --> 3/37 = 97.3 (major-diesis)
16875:16384 = 51.1 + 46.2 --> 3/37 = 97.3 (negri-comma)
250:243 = 49.2 - 49.2 --> 0/37 = 0.0 (maximal-diesis)
128:125 = 41.1 - 8.6 --> 1/37 = 32.4 (enharmonic-diesis)
34171875:33554432 = 31.6 + 98.2 --> 4/37 = 129.7 (ampersand-comma)
3125:3072 = 29.6 + 2.8 --> 1/37 = 32.4 (magic-comma)
20000:19683 = 27.7 - 92.5 --> -2/37 = - 64.9 (tetracot-comma)
81:80 = 21.5 + 43.4 --> 2/37 = 64.9 (syntonic-comma)
2048:2025 = 19.6 - 52.0 --> -1/37 = - 32.4 (diaschisma)
393216:390625 = 11.4 - 11.4 --> 0/37 = 0.0 (wuerschmidt-comma)
2109375:2097152 = 10.1 + 54.8 --> 2/37 = 64.9 (semicomma)
15625:15552 = 8.1 - 40.5 --> -1/37 = - 32.4 (kleisma)
32805:32768 = 2.0 + 95.3 --> 3/37 = 97.3 (skhisma)
76294:76256 = 0.9 - 260.3 --> -8/37 = - 259.5 (ennealimma (~ratio))
292300:292297 = 0.0 -1005.4 --> -31/37 = -1005.4 (atom (~ratio))
7-limit
ratio cents error edo cents name
36:35 = 48.8 +16.1 --> 2/37 = 64.9 (septimal-diesis)
49:48 = 35.7 - 3.3 --> 1/37 = 32.4 (slendro diesis (7/6 : 8/7))
50:49 = 35.0 - 2.5 --> 1/37 = 32.4 (tritonic diesis, jubilisma)
64:63 = 27.3 -27.3 --> 0/37 = 0.0 (septimal-comma)
225:224 = 7.7 +24.7 --> 1/37 = 32.4 (septimal-kleisma)
11-limit
ratio cents error edo cents name
22:21 = 80.5 -15.7 --> 2/37 = 64.9 ()
33:32 = 53.3 +11.6 --> 2/37 = 64.9 (undecimal-diesis)
45:44 = 38.9 +26.0 --> 2/37 = 64.9 ()
8192:8019 = 37.0 -69.4 --> -1/37 = -32.4 (pyth dim-5th: 11/8)
55:54 = 31.8 -31.8 --> 0/37 = 0.0 ()
56:55 = 31.2 + 1.2 --> 1/37 = 32.4 ()
99:98 = 17.6 +14.9 --> 1/37 = 32.4 (mothwellsma)
100:99 = 17.4 -17.4 --> 0/37 = 0.0 (ptolemisma)
121:120 = 14.4 -14.4 --> 0/37 = 0.0 (biyatisma (11/10 : 12/11))
13-limit
ratio cents error edo cents name
40:39 = 43.8 -11.4 --> 1/37 = 32.4 ((5/3 : 13/8))
65:64 = 26.8 + 5.6 --> 1/37 = 32.4 ((13/8 : 8/5))
6656:6561 = 24.9 -89.8 --> -2/37 = -64.9 (13/8 : pyth aug-5th)
91:90 = 19.1 -19.1 --> 0/37 = 0.0 (superleap)
144:143 = 12.1 +20.4 --> 1/37 = 32.4 ((18/11 : 13/8))
169:168 = 10.3 -10.3 --> 0/37 = 0.0 (dhanvantarisma)
Below is a graph showing the degrees of 37-edo as the Y-axis grid, with the pitch of the JI ratios given in the table above plotted against it:
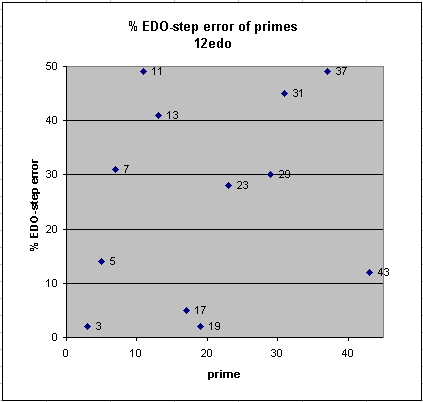
Below are graphs of the error of 12-edo and 37-edo for approximations to the prime-factors up to 43, given as a percentage of one degree of each tuning. It can easily be seen that compared to 12-edo, 37-edo's approximations of the prime-factors are:
However, Monzo feels that since jazz musical styles generally place less harmonic emphasis on the 3-identity of a chord (often omitting it entirely), 37-edo offers a great avenue of exploration for microtonality in jazz.
|
|
The tonalsoft.com website is almost entirely the work of one person: me, Joe Monzo. Please reward me for my knowledge and effort by selecting the highest level of financial support that you can afford. Thank you.