22-edo (also called 22-ET or 22-tone equal-temperament, when used as a temperament of JI), divides the octave into 22 equal degrees, each having a logarithmic size of exactly 54 + 6/11 (= ~54.54_) cents.
Used as a temperament, 22-edo is a fairly small cardinality which gives a fairly good approximation to 11-limit JI:
- Its best mapping of prime-factor 3 is to 35 degrees of 22-edo (35\22); narrowing that by one octave (i.e., subtracting 22 degrees: 35 - 22 = 13), its mapping of the perfect-5th of 3:2 ratio is to 13 degrees of 22-edo (13\22), which equals exactly 709 + 1/11 (= ~709.09_) cents, with an absolute prime-error of ~+7.1 cents and a relative prime-error of +13% of a 22-edo degree.
- Its best mapping of prime-factor 5 is to 51\22; narrowing that by 2 octaves (i.e., subtracting 2 * 22 = 44 degrees: 51 - 44 = 7), its mapping of the just major-3rd of 5:4 ratio is to 7\22, which equals exactly 381 + 9/11 (= ~381.81_) cents, with an absolute prime-error of ~-4.5 cents and a relative prime-error of ~-8% of a 22-edo degree.
- Its best mapping of prime-factor 7 is to 62\22; narrowing that by 2 octaves (i.e., subtracting 2 * 22 = 44 degrees: 62 - 44 = 18), its mapping of the harmonic-7th of 7:4 ratio is to 18\22, which equals exactly 981 + 9/11 (= ~981.81_) cents, with an absolute prime-error of ~13 cents and a relative prime-error of ~24% of a 22-edo degree.
- Its best mapping of prime-factor 11 is to 76\22; narrowing that by 3 octaves (i.e., subtracting 3 * 22 = 66 degrees: 76 - 66 = 10), its mapping of the _ of 11:8 ratio is to 10\22, which equals exactly 545 + 5/11 (= ~545.45_) cents, with an absolute prime-error of ~-5.9 cents and a relative prime-error of -11% of a 22-edo degree.
Note that 22edo's mappings of prime-factors 3 and 7 are larger (wider, positive), while its mappings of 5 and 11 are smaller (narrow, negative) and both of the narrower mappings have less error than the wider mappings.
22edo also gives outstanding approximations of two of the higher harmonics: 31 and 53. The 31:16 ratio maps to 21\22 (i.e., approximately a quarter-tone smaller than the 2:1 octave), with an absolute prime-error of ~+0.4 cents and a relative prime-error of ~+0.8% of a 22-edo degree. The 53:32 ratio maps to 16\22 with an absolute prime-error of ~-0.8 cents and a relative prime-error of ~1.4% of a 22-edo degree.
Below is a graphic comparing the absolute prime-error (i.e., not showing whether it is positive or negative) of the familiar 12edo with that of 22edo for the 43-prime-limit:
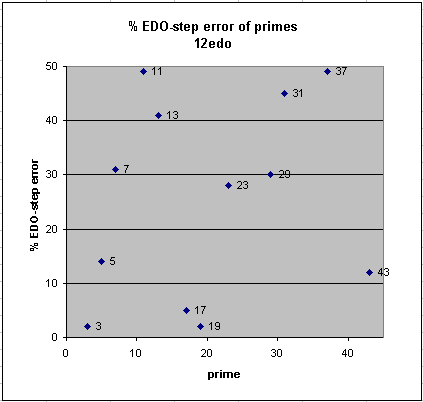
|

|
One popular method of notating 22-edo on a standard 5-line musical staff is called "up/down notation", using the standard A B C D E F G nominals in such a way that what appears to be a whole-tone as A:B, C:D, D:E, F:G, G:A spans 4 degrees of 22-edo (4\22), and what appears to be a diatonic-semitone as B:C, E:F, or any nominal paired with either a sharp on the note below or a flat on the note above, spans 1 degree of 22-edo (1\22), and employing as additional accidentals up or down arrows, either alone or attached to sharps or flats as necessary. There is an abundance of enharmonic-equivalents in this notation, only the most basic of which are shown in the graphic below:
22edo up/down notation, on standard 5-line musical staff

Another notation system available for 22-edo is sagittal, which operates exactly the same as up/down but employs different accidentals.
Below is a table showing precise values for the mappings of 22-edo in 41-limit JI, with several example ratios and commas:
=======================================
edomap.py (c)2008-12-23 by Joseph Monzo
=======================================
Finds the EDO mappings for a set of ratios
please enter edo: 22
22 -edo floating-point mappings:
prime edo-steps step-error edo-map
2 = 22.000000 +0.00 --> 22
3 = 34.869175 +0.13 --> 35
5 = 51.082418 -0.08 --> 51
7 = 61.761808 +0.24 --> 62
11 = 76.107496 -0.11 --> 76
13 = 81.409674 -0.41 --> 81
17 = 89.924183 +0.08 --> 90
19 = 93.454405 -0.45 --> 93
23 = 99.518363 +0.48 --> 100
29 = 106.875582 +0.12 --> 107
31 = 108.992319 +0.01 --> 109
37 = 114.607974 +0.39 --> 115
41 = 117.866144 +0.13 --> 118
43 = 119.377825 -0.38 --> 119
47 = 122.200955 -0.20 --> 122
53 = 126.014250 -0.01 --> 126
integer (i.e., true) mappings, compared with cents-value of actual prime
map 2 --> 22 = 1200.000000 cents <-- 1200.000000 + 0.0 cents
map 3 --> 35 = 1909.090909 cents <-- 1901.955001 + 7.1 cents
map 5 --> 51 = 2781.818182 cents <-- 2786.313714 - 4.5 cents
map 7 --> 62 = 3381.818182 cents <-- 3368.825906 +13.0 cents
map 11 --> 76 = 4145.454545 cents <-- 4151.317942 - 5.9 cents
map 13 --> 81 = 4418.181818 cents <-- 4440.527662 -22.3 cents
map 17 --> 90 = 4909.090909 cents <-- 4904.955410 + 4.1 cents
map 19 --> 93 = 5072.727273 cents <-- 5097.513016 -24.8 cents
map 23 --> 100 = 5454.545455 cents <-- 5428.274347 +26.3 cents
map 29 --> 107 = 5836.363636 cents <-- 5829.577194 + 6.8 cents
map 31 --> 109 = 5945.454545 cents <-- 5945.035572 + 0.4 cents
map 37 --> 115 = 6272.727273 cents <-- 6251.344039 +21.4 cents
map 41 --> 118 = 6436.363636 cents <-- 6429.062406 + 7.3 cents
map 43 --> 119 = 6490.909091 cents <-- 6511.517706 -20.6 cents
map 47 --> 122 = 6654.545455 cents <-- 6665.506622 -11.0 cents
map 53 --> 126 = 6872.727273 cents <-- 6873.504545 - 0.8 cents
--------------
examples:
ratio --> 22 -edo mapping:
ratio cents error edo cents name
2:1 = 1200.0 + 0.0 --> 22\22 = 1200.0 (octave)
31:16 = 1145.0 + 0.4 --> 21\22 = 1145.5 (31st harmonic)
243:128 = 1109.8 +35.7 --> 21\22 = 1145.5 (pythagorean major-7th)
15:8 = 1088.3 + 2.6 --> 20\22 = 1090.9 (just major-7th, 5*3)
4096:2187 = 1086.3 -50.0 --> 19\22 = 1036.4 (pythagorean diminished-8ve)
13:7 = 1071.7 -35.3 --> 19\22 = 1036.4 (tridecimal superminor-7th)
11:6 = 1049.4 -13.0 --> 19\22 = 1036.4 (undecimal submajor-7th)
20:11 = 1035.0 + 1.4 --> 19\22 = 1036.4 (undecimal superminor-7th)
29:16 = 1029.6 + 6.8 --> 19\22 = 1036.4 (29th harmonic)
9:5 = 1017.6 +18.8 --> 19\22 = 1036.4 (just minor-7th)
16:9 = 996.1 -14.3 --> 18\22 = 981.8 (pythagorean minor-7th)
7:4 = 968.8 +13.0 --> 18\22 = 981.8 (7th harmonic)
12:7 = 933.1 - 5.9 --> 17\22 = 927.3 (septimal supermajor-6th)
27:16 = 905.9 +21.4 --> 17\22 = 927.3 (pythagorean major-6th)
5:3 = 884.4 -11.6 --> 16\22 = 872.7 (just major-6th)
53:32 = 873.5 - 0.8 --> 16\22 = 872.7 (53rd harmonic)
18:11 = 852.6 +20.1 --> 16\22 = 872.7 (undecimal neutral-6th)
6561:4096 = 815.6 +57.1 --> 16\22 = 872.7 (pythagorean augmented-5th)
13:8 = 840.5 -22.3 --> 15\22 = 818.2 (13th harmonic)
8:5 = 813.7 + 4.5 --> 15\22 = 818.2 (just minor-6th)
128:81 = 792.2 -28.5 --> 14\22 = 763.6 (pythagorean minor-6th)
11:7 = 782.5 -18.9 --> 14\22 = 763.6 (undecimal augmented-5th)
25:16 = 772.6 - 9.0 --> 14\22 = 763.6 (just augmented-5th)
14:9 = 764.9 - 1.3 --> 14\22 = 763.6 (septimal subminor-9th)
3:2 = 702.0 + 7.1 --> 13\22 = 709.1 (perfect-5th)
47:32 = 665.5 -11.0 --> 12\22 = 654.5 (47th harmonic)
16:11 = 648.7 + 5.9 --> 12\22 = 654.5 (11th subharmonic)
23:16 = 628.3 +26.3 --> 12\22 = 654.5 (23rd harmonic)
729:512 = 611.7 +42.8 --> 12\22 = 654.5 (pythagorean augmented-4th)
10:7 = 617.5 -17.5 --> 11\22 = 600.0 (septimal large-tritone)
7:5 = 582.5 +17.5 --> 11\22 = 600.0 (septimal small-tritone)
1024:729 = 588.3 -42.8 --> 10\22 = 545.5 (pythagorean diminished-5th)
11:8 = 551.3 - 5.9 --> 10\22 = 545.5 (11th harmonic)
43:32 = 511.5 -20.6 --> 9\22 = 490.9 (43rd harmonic)
4:3 = 498.0 - 7.1 --> 9\22 = 490.9 (perfect-4th)
21:16 = 470.8 +20.1 --> 9\22 = 490.9 (septimal-4th, 7*3)
9:7 = 435.1 + 1.3 --> 8\22 = 436.4 (septimal supermajor-3rd)
41:32 = 429.1 + 7.3 --> 8\22 = 436.4 (41st harmonic)
14:11 = 417.5 +18.9 --> 8\22 = 436.4 (undecimal diminished-4th)
81:64 = 407.8 +28.5 --> 8\22 = 436.4 (pythagorean major-3rd)
5:4 = 386.3 - 4.5 --> 7\22 = 381.8 (just major-3rd)
19683:16384 = 317.6 +64.2 --> 7\22 = 381.8 (pythagorean augmented-2nd)
8192:6561 = 384.4 -57.1 --> 6\22 = 327.3 (pythagorean diminished-4th)
11:9 = 347.4 -20.1 --> 6\22 = 327.3 (undecimal neutral-3rd)
39:32 = 342.5 -15.2 --> 6\22 = 327.3 (39th harmonic, 13*3)
6:5 = 315.6 +11.6 --> 6\22 = 327.3 (just minor-3rd)
19:16 = 297.5 -24.8 --> 5\22 = 272.7 (19th harmonic)
32:27 = 294.1 -21.4 --> 5\22 = 272.7 (pythagorean minor-3rd)
13:11 = 289.2 -16.5 --> 5\22 = 272.7 (tridecimal diminished-3rd)
75:64 = 274.6 - 1.9 --> 5\22 = 272.7 (75th harmonic = 15:16 * 5:4)
7:6 = 266.9 + 5.9 --> 5\22 = 272.7 (septimal subminor-7th)
37:32 = 251.3 +21.4 --> 5\22 = 272.7 (37th harmonic)
8:7 = 231.2 -13.0 --> 4\22 = 218.2 (septimal tone)
9:8 = 203.9 +14.3 --> 4\22 = 218.2 (pythagorean major-2nd/tone)
10:9 = 182.4 -18.8 --> 3\22 = 163.6 (just minor-tone)
11:10 = 165.0 - 1.4 --> 3\22 = 163.6 (undecimal small-tone/submajor-2nd)
35:32 = 155.1 + 8.5 --> 3\22 = 163.6 (35th harmonic, 7*5)
12:11 = 150.6 +13.0 --> 3\22 = 163.6 (undecimal large-semitone)
14:13 = 128.3 +35.3 --> 3\22 = 163.6 (tridecimal major-2nd)
2187:2048 = 113.7 +50.0 --> 3\22 = 163.6 (pythagorean augmented-prime/apotome)
13:12 = 138.6 -29.5 --> 2\22 = 109.1 (tridecimal minor-2nd)
15:14 = 119.4 -10.4 --> 2\22 = 109.1 (septimal chromatic-semitone)
16:15 = 111.7 - 2.6 --> 2\22 = 109.1 (just diatonic-semitone)
17:16 = 105.0 + 4.1 --> 2\22 = 109.1 (septendecimal semitone)
256:243 = 90.2 -35.7 --> 1\22 = 54.5 (pythagorean minor-2nd/limma)
25:24 = 70.7 -16.1 --> 1\22 = 54.5 (just chromatic-semitone)
33:32 = 53.3 + 1.3 --> 1\22 = 54.5 (33rd harmonic, 11*3)
1:1 = 0.0 + 0.0 --> 0\22 = 0.0 (prime)
some commas:
3-limit:
531441:524288 = 23.5 +85.6 --> 2\22 = 109.1 (pythagorean-comma)
5-limit:
648:625 = 62.6 +46.5 --> 2\22 = 109.1 (major-diesis)
250:243 = 49.2 -49.2 --> 0\22 = 0.0 (maximal-diesis)
128:125 = 41.1 +13.5 --> 1\22 = 54.5 (enharmonic-diesis)
34171875:33554432 = 31.6 +23.0 --> 1\22 = 54.5 (ampersand-comma)
3125:3072 = 29.6 -29.6 --> 0\22 = 0.0 (magic-comma)
81:80 = 21.5 +33.0 --> 1\22 = 54.5 (syntonic-comma)
2048:2025 = 19.6 -19.6 --> 0\22 = 0.0 (diaschisma)
2109375:2097152 = 10.1 -10.1 --> 0\22 = 0.0 (semicomma)
15625:15552 = 8.1 -62.7 --> -1\22 = -54.5 (kleisma)
32805:32768 = 2.0 +52.6 --> 1\22 = 54.5 (skhisma)
7-limit:
36:35 = 48.8 + 5.8 --> 1\22 = 54.5 (septimal-diesis)
49:48 = 35.7 +18.8 --> 1\22 = 54.5 (septimal-comma-3 - 7/6 : 8/7)
50:49 = 35.0 -35.0 --> 0\22 = 0.0 (septimal-comma-2)
64:63 = 27.3 -27.3 --> 0\22 = 0.0 (septimal-comma)
225:224 = 7.7 - 7.7 --> 0\22 = 0.0 (septimal-kleisma)
11-limit:
22:21 = 80.5 -26.0 --> 1\22 = 54.5 ()
33:32 = 53.3 + 1.3 --> 1\22 = 54.5 (undecimal-diesis)
45:44 = 38.9 +15.6 --> 1\22 = 54.5 ()
55:54 = 31.8 -31.8 --> 0\22 = 0.0 ()
56:55 = 31.2 +23.4 --> 1\22 = 54.5 ()
121:120 = 14.4 -14.4 --> 0\22 = 0.0 (11/10 : 12/11 comma)
22-edo calculator
Please make a donation to help keep Tonalsoft online.
Thank you!
