53-edo (also called 53-ET or 53-tone equal-temperament, when used as a temperament of JI), divides the octave into 53 equal degrees, each having a logarithmic size of exactly 22 + 34/53 (= ~22.64151) cents.
Used as a temperament, 53-edo is a fairly large cardinality which gives a very good approximiation of "classic" 5-limit JI, and an truly outstanding approximation of 3-limit JI (i.e., pythagorean tuning):
- Its best mapping of prime-factor 3 is to 84 degrees of 53-edo (84\53); narrowing that by one octave (i.e., subtracting 53 degrees: 84 - 53 = 31), its best mapping of the perfect-5th of 3:2 ratio is to 31 degrees of 53-edo (31\53), which equals exactly 701 + 47/53 (= ~701.887) cents, with an absolute prime-error in cents of only ~-0.068 (~-3/44 or less accurately ~-1/15) cent, and a relative prime-error of ~-0.3012538% (i.e., less than ~-1/3 of a percent) of a 53-edo degree.
- Its best mapping of prime-factor 5 is to 123\53; narrowing that by 2 octaves (i.e., subtracting 2 * 53 = 106 degrees: 123 - 106 = 17), its best mapping of the just major-3rd of 5:4 ratio is to 17\53, which equals exactly 384 + 48/53 (= ~384.90566 or less accurately 384 + 10/11) cents, with an absolute prime-error of ~-1.408 cents and a relative prime-error of ~-6.219% of a 53-edo degree.
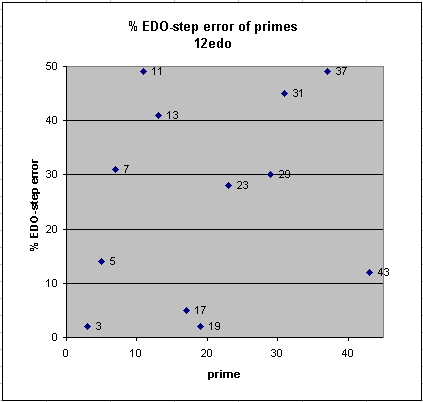
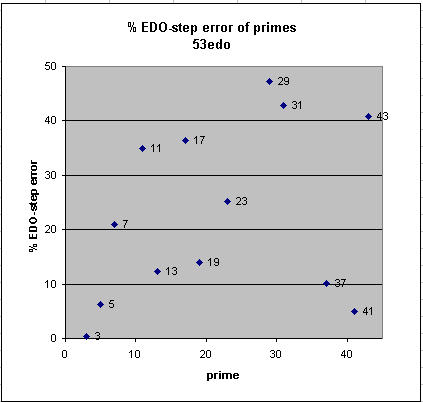
- Within the 43-limit, it also provides an excellent mapping of prime 41, good mappings of primes 13, 19, and 37, mediocre mappings of 7 and 23, fairly poor mappings of 11 and 17, and terrible mappings of 29, 31, and 43.
Below is a graphic comparing the absolute prime-error (i.e., not showing whether it is positive or negative) of the familiar 12edo with that of 53edo:
|
|
Because of its excellent ability to represent 5-limit JI, 53edo has been advocated often (particularly in the late 1800s and early 1900s) as a means for expansion of the tonal palette beyond 12edo, particularly in order to provide more concordant harmonies, and is still advocated in the early 21st century by many microtonalists as an "ultimate tuning".
If the intention is to use 53edo to represent 5-limit JI, a very simple version of HEWM notation can be used, wherein the pythagorean chain-of-5ths is notated by the usual 7 nominals (A B C D E F G) which may be accompanied by a flat b, sharp #, double-flat bb, or double-sharp x, notes which differ from pythagorean by a syntonic-comma (81:80 ratio) are accompanied by a minus - or plus +, or multiples thereof in the case of a difference from pythagorean by multiple syntonic-commas.
Used as a unit of interval measurement, one degree of 53edo has been named a "mercator" by Joseph Monzo.
Below is a table showing precise values for the mappings of 53-edo in 43-limit JI, with several example ratios and commas:
====================================
edomap.py (c)2008-12-23 by Joseph Monzo
====================================
Finds the EDO mappings for a set of ratios
=============== new run =====================
please enter edo: 53
any displaced mappings? ... 0=no, 1=yes : 0
53 -edo floating-point mappings:
prime edo-steps step-error edo-map
2 = 53.000000 +0.00 --> 53
3 = 84.003013 -0.00 --> 84
5 = 123.062189 -0.06 --> 123
7 = 148.789811 +0.21 --> 149
11 = 183.349876 -0.35 --> 183
13 = 196.123305 -0.12 --> 196
17 = 216.635531 +0.36 --> 217
19 = 225.140158 -0.14 --> 225
23 = 239.748784 +0.25 --> 240
29 = 257.472993 -0.47 --> 257
31 = 262.572404 +0.43 --> 263
37 = 276.101028 -0.10 --> 276
41 = 283.950256 +0.05 --> 284
43 = 287.592032 +0.41 --> 288
integer (i.e., true) mappings, compared with cents-value of actual prime
map 2 --> 53 = 1200.000000 cents <-- 1200.000000 +0.0 cents
map 3 --> 84 = 1901.886792 cents <-- 1901.955001 -0.1 cents
map 5 --> 123 = 2784.905660 cents <-- 2786.313714 -1.4 cents
map 7 --> 149 = 3373.584906 cents <-- 3368.825906 +4.8 cents
map 11 --> 183 = 4143.396226 cents <-- 4151.317942 -7.9 cents
map 13 --> 196 = 4437.735849 cents <-- 4440.527662 -2.8 cents
map 17 --> 217 = 4913.207547 cents <-- 4904.955410 +8.3 cents
map 19 --> 225 = 5094.339623 cents <-- 5097.513016 -3.2 cents
map 23 --> 240 = 5433.962264 cents <-- 5428.274347 +5.7 cents
map 29 --> 257 = 5818.867925 cents <-- 5829.577194 -10.7 cents
map 31 --> 263 = 5954.716981 cents <-- 5945.035572 +9.7 cents
map 37 --> 276 = 6249.056604 cents <-- 6251.344039 -2.3 cents
map 41 --> 284 = 6430.188679 cents <-- 6429.062406 +1.1 cents
map 43 --> 288 = 6520.754717 cents <-- 6511.517706 +9.2 cents
--------------
examples:
ratio --> 53 -edo mapping:
mappings of some ratios:
ratio cents error edo cents name
2:1 = 1200.000 +0.000 --> 53/53 = 1200.000 (octave) <>
31:16 = 1145.036 +9.681 --> 51/53 = 1154.717 (31st harmonic) <>
21:11 = 1119.463 +12.613 --> 50/53 = 1132.075 (undecimal diminished-8ve) <>
243:128 = 1109.775 -0.341 --> 49/53 = 1109.434 (pythagorean major-7th) <>
15:8 = 1088.269 -1.476 --> 48/53 = 1086.792 (15th harmonic, just major-7th, 5*3) <>
4096:2187 = 1086.315 +0.477 --> 48/53 = 1086.792 (pythagorean diminished-8ve) <>
13:7 = 1071.702 -7.551 --> 47/53 = 1064.151 (tridecimal superminor-7th) <>
24:13 = 1061.427 +2.724 --> 47/53 = 1064.151 (tridecimal major-7th) <>
11:6 = 1049.363 -7.854 --> 46/53 = 1041.509 (undecimal submajor[neutral]-7th) <>
20:11 = 1034.996 +6.514 --> 46/53 = 1041.509 (undecimal superminor[neutral]-7th) <>
29:16 = 1029.577 -10.709 --> 45/53 = 1018.868 (29th harmonic) <>
9:5 = 1017.596 +1.272 --> 45/53 = 1018.868 (just minor-7th) <>
16:9 = 996.090 +0.136 --> 44/53 = 996.226 (pythagorean minor-7th) <>
7:4 = 968.826 +4.759 --> 43/53 = 973.585 (7th harmonic, septimal subminor-7th) <>
19:11 = 946.195 +4.748 --> 42/53 = 950.943 (nondecimal supermajor-6th) <>
12:7 = 933.129 -4.827 --> 41/53 = 928.302 (septimal supermajor-6th) <>
22:13 = 910.790 -5.130 --> 40/53 = 905.660 (tridecimal augmented-6th) <>
27:16 = 905.865 -0.205 --> 40/53 = 905.660 (27th harmonic, pythagorean major-6th) <>
5:3 = 884.359 -1.340 --> 39/53 = 883.019 (just major-6th) <>
18:11 = 852.592 +7.785 --> 38/53 = 860.377 (undecimal superminor[neutral]-6th) <>
13:8 = 840.528 -2.792 --> 37/53 = 837.736 (13th harmonic) <>
21:13 = 830.253 +7.483 --> 37/53 = 837.736 (tridecimal ?) <>
6561:4096 = 815.640 -0.546 --> 36/53 = 815.094 (pythagorean augmented-5th) <>
8:5 = 813.686 +1.408 --> 36/53 = 815.094 (just minor-6th) <>
128:81 = 792.180 +0.273 --> 35/53 = 792.453 (pythagorean minor-6th) <>
11:7 = 782.492 -12.681 --> 34/53 = 769.811 (undecimal augmented-5th) <>
25:16 = 772.627 -2.816 --> 34/53 = 769.811 (25th harmonic, just augmented-5th) <>
14:9 = 764.916 +4.895 --> 34/53 = 769.811 (septimal subminor-6th) <>
17:11 = 753.637 +16.174 --> 34/53 = 769.811 (septendecimal diminished-6th) <>
20:13 = 745.786 +1.384 --> 33/53 = 747.170 (tridecimal augmented-5th) <>
3:2 = 701.955 -0.068 --> 31/53 = 701.887 (perfect-5th) <>
19:13 = 656.985 -0.382 --> 29/53 = 656.604 (nondecimal doubly-augmented-4th) <>
16:11 = 648.682 +7.922 --> 29/53 = 656.604 (11th subharmonic, undecimal diminished-4th) <>
13:9 = 636.618 -2.655 --> 28/53 = 633.962 (tridecimal diminished-5th) <>
23:16 = 628.274 +5.688 --> 28/53 = 633.962 (23rd harmonic) <>
10:7 = 617.488 -6.167 --> 27/53 = 611.321 (septimal large-tritone) <>
729:512 = 611.730 -0.409 --> 27/53 = 611.321 (pythagorean augmented-4th) <>
64:45 = 609.776 +1.544 --> 27/53 = 611.321 (just diminished-5th) <>
45:32 = 590.224 -1.544 --> 26/53 = 588.679 (just augmented-4th) <>
1024:729 = 588.270 +0.409 --> 26/53 = 588.679 (pythagorean diminished-5th) <>
7:5 = 582.512 +6.167 --> 26/53 = 588.679 (septimal small-tritone) <>
18:13 = 563.382 +2.655 --> 25/53 = 566.038 (tridecimal augmented-4th) <>
11:8 = 551.318 -7.922 --> 24/53 = 543.396 (11th harmonic, undecimal sub-augmented-4th) <>
15:11 = 536.951 +6.445 --> 24/53 = 543.396 (undecimal large-4th) <>
43:32 = 511.518 +9.237 --> 23/53 = 520.755 (43rd harmonic) <>
4:3 = 498.045 +0.068 --> 22/53 = 498.113 (perfect-4th) <>
21:16 = 470.781 +4.691 --> 21/53 = 475.472 (21st harmonic, septimal-4th, 7*3) <>
17:13 = 464.428 +11.044 --> 21/53 = 475.472 (septendecimal 4th) <>
13:10 = 454.214 -1.384 --> 20/53 = 452.830 (tridecimal diminished-4th) <>
9:7 = 435.084 -4.895 --> 19/53 = 430.189 (septimal supermajor-3rd) <>
41:32 = 429.062 +1.126 --> 19/53 = 430.189 (41st harmonic) <>
14:11 = 417.508 +12.681 --> 19/53 = 430.189 (undecimal diminished-4th) <>
81:64 = 407.820 -0.273 --> 18/53 = 407.547 (pythagorean major-3rd) <>
5:4 = 386.314 -1.408 --> 17/53 = 384.906 (5th harmonic, just major-3rd) <>
8192:6561 = 384.360 +0.546 --> 17/53 = 384.906 (pythagorean diminished-4th) <>
16:13 = 359.472 +2.792 --> 16/53 = 362.264 (tridecimal major[neutral]-3rd) <>
11:9 = 347.408 -7.785 --> 15/53 = 339.623 (undecimal neutral-3rd) <>
39:32 = 342.483 -2.860 --> 15/53 = 339.623 (39th harmonic, 13*3) <>
19683:16384 = 317.595 -0.614 --> 14/53 = 316.981 (pythagorean augmented-2nd) <>
6:5 = 315.641 +1.340 --> 14/53 = 316.981 (just minor-3rd) <>
19:16 = 297.513 -3.173 --> 13/53 = 294.340 (19th harmonic) <>
32:27 = 294.135 +0.205 --> 13/53 = 294.340 (pythagorean minor-3rd) <>
13:11 = 289.210 +5.130 --> 13/53 = 294.340 (tridecimal diminished-3rd) <>
75:64 = 274.582 -2.884 --> 12/53 = 271.698 (just augmented-2nd) <>
7:6 = 266.871 +4.827 --> 12/53 = 271.698 (septimal subminor-3rd) <>
37:32 = 251.344 -2.287 --> 11/53 = 249.057 (37th harmonic) <>
15:13 = 247.741 +1.316 --> 11/53 = 249.057 (tridecimal augmented[neutral]-2nd) <>
8:7 = 231.174 -4.759 --> 10/53 = 226.415 (septimal tone, supermajor-2nd) <>
9:8 = 203.910 -0.136 --> 9/53 = 203.774 (pythagorean major-2nd/tone) <>
10:9 = 182.404 -1.272 --> 8/53 = 181.132 (just minor-tone) <>
11:10 = 165.004 -6.514 --> 7/53 = 158.491 (undecimal small-tone/submajor-2nd) <>
35:32 = 155.140 +3.351 --> 7/53 = 158.491 (35th harmonic, 7*5) <>
12:11 = 150.637 +7.854 --> 7/53 = 158.491 (undecimal large-semitone) <>
13:12 = 138.573 -2.724 --> 6/53 = 135.849 (tridecimal minor-2nd) <>
14:13 = 128.298 +7.551 --> 6/53 = 135.849 (tridecimal major-2nd) <>
15:14 = 119.443 -6.235 --> 5/53 = 113.208 (septimal chromatic-semitone) <>
2187:2048 = 113.685 -0.477 --> 5/53 = 113.208 (pythagorean augmented-prime/apotome) <>
16:15 = 111.731 +1.476 --> 5/53 = 113.208 (just diatonic-semitone) <>
17:16 = 104.955 +8.252 --> 5/53 = 113.208 (17th harmonic, septendecimal semitone) <>
256:243 = 90.225 +0.341 --> 4/53 = 90.566 (pythagorean minor-2nd/limma) <>
25:24 = 70.672 -2.748 --> 3/53 = 67.925 (just chromatic-semitone) <>
33:32 = 53.273 -7.990 --> 2/53 = 45.283 (33rd harmonic, 11*3) <>
1:1 = 0.000 +0.000 --> 0/53 = 0.000 (prime) <>
....................
some commas:
3-limit
ratio cents error edo cents name
256:243 = 90.225 +0.341 --> 4/53 = 90.566 (pythagorean-limma/blackwood-comma) <limmic>
1342178:1291402 = 66.765 +1.160 --> 3/53 = 67.925 (gothic-comma/17-comma (~ratio, monzo=[27 -17>)) <neogothic>
70368744:68630377 = 43.305 +1.978 --> 2/53 = 45.283 (mystery-comma/29-comma (~ratio, monzo=[46 -29>)) <mystery>
531441:524288 = 23.460 -0.819 --> 1/53 = 22.642 (pythagorean-comma (exact ratio)) <compton/aristoxenean>
36893:36473 = 19.845 +2.797 --> 1/53 = 22.642 (countercomp-comma/41-comma (~ratio, monzo=[65 -41>)) <countercomp>
19383246:19342813 = 3.615 -3.615 --> 0/53 = 0.000 (mercator-comma (~ratio, monzo=[-84 53>)) <>
19303426:19302583 = 0.076 -45.359 --> -2/53 = -45.283 (satanic-comma (~ratio, monzo=[-1054 665>)) <satanic>
5-limit
ratio cents error edo cents name
27:25 = 133.238 +2.611 --> 6/53 = 135.849 (large-limma/acute-min2/bug-comma) <bug>
16:15 = 111.731 +1.476 --> 5/53 = 113.208 (classic-ji-diatonic-semitone/father-comma) <father>
135:128 = 92.179 -1.613 --> 4/53 = 90.566 (ptolemaic-chroma/major-limma/mavila-comma (exact ratio, monzo=[-7 3 1>)) <mavila>
1220703:1162261 = 84.933 -17.009 --> 3/53 = 67.925 (bohpier-comma (~ratio, monzo=[0 -19 13>)) <13ed3>
6561:6250 = 84.071 +6.495 --> 4/53 = 90.566 (ripple-comma (exact ratio, monzo=[-1 8 -5>)) <ripple>
390625:373248 = 78.780 -10.855 --> 3/53 = 67.925 (doublewide-comma (exact ratio, monzo=[-9 -6 8>)) <doublewide>
25:24 = 70.672 -2.748 --> 3/53 = 67.925 (classic-ji-chroma/dicot-comma (exact ratio, monzo=[-3 -1 2>)) <dicot>
648:625 = 62.565 +5.359 --> 3/53 = 67.925 (major-diesis/diminished-comma) <diminished>
262144:253125 = 60.611 +7.313 --> 3/53 = 67.925 (passion-comma (exact ratio, monzo=[18 -4 -5>)) <passion>
16875:16384 = 51.120 -5.837 --> 2/53 = 45.283 (negri-comma) <negri>
250:243 = 49.166 -3.883 --> 2/53 = 45.283 (maximal-diesis) <porcupine>
1638400:1594323 = 47.212 -1.929 --> 2/53 = 45.283 (immunity-comma (exact ratio, monzo=[16 -13 2>)) <immunity>
128:125 = 41.059 +4.224 --> 2/53 = 45.283 (enharmonic-diesis/augmented-comma) <augmented>
48828125:47775744 = 37.721 -15.079 --> 1/53 = 22.642 (sycamore-comma (exact ratio, monzo=[-16 -6 11>)) <sycamore>
1594323:1562500 = 34.905 +10.378 --> 2/53 = 45.283 (unicorn-comma (exact ratio, monzo=[-2 13 -8>)) <>
1990656:1953125 = 32.952 +12.331 --> 2/53 = 45.283 (valentine-comma (exact ratio, monzo=[13 5 -9>)) <>
34171875:33554432 = 31.567 -8.926 --> 1/53 = 22.642 (ampersand-comma) <5-limit miracle>
3125:3072 = 29.614 -6.972 --> 1/53 = 22.642 (magic-comma) <magic>
20000:19683 = 27.660 -5.018 --> 1/53 = 22.642 (tetracot-comma) <tetracot>
81:80 = 21.506 +1.135 --> 1/53 = 22.642 (syntonic-comma) <meantone>
2048:2025 = 19.553 +3.089 --> 1/53 = 22.642 (diaschisma) <diaschismic/srutal/pajara>
67108864:66430125 = 17.599 +5.043 --> 1/53 = 22.642 (misty-comma (exact ratio, monzo=[26 -12 -3>)) <misty>
129140163:128000000 = 15.353 +7.289 --> 1/53 = 22.642 (graviton (exact ratio, monzo=[-13 17 -6>)) <gravity>
78732:78125 = 13.399 +9.242 --> 1/53 = 22.642 (sensipent-comma) <sensipent>
393216:390625 = 11.445 +11.196 --> 1/53 = 22.642 (wuerschmidt-comma) <wuerschmidt>
2109375:2097152 = 10.061 -10.061 --> 0/53 = 0.000 (semicomma/fokker-comma (exact ratio, monzo=[-21 3 7>)) <orson>
4294967296:4271484375 = 9.492 +13.150 --> 1/53 = 22.642 (escapade-comma (exact ratio, monzo=[32 -7 -9>)) <escapade>
15625:15552 = 8.107 -8.107 --> 0/53 = 0.000 (kleisma/semicomma-majeur (exact ratio, monzo=[-6 -5 6>)) <kleismic>
476837:474989 = 6.723 -29.364 --> -1/53 = -22.642 (mutt-comma (~ratio, monzo=[-44 -3 21>)) <mutt>
1600000:1594323 = 6.154 -6.154 --> 0/53 = 0.000 (amity-comma (exact ratio, monzo=[9 -13 5>) <amity>
1224440064:1220703125 = 5.292 +17.350 --> 1/53 = 22.642 (parakleisma (exact ratio, monzo=[8 14 -13>) <parakleismic>
1048576:1046035 = 4.200 -4.200 --> 0/53 = 0.000 (vulture-comma (~ratio, monzo=[24 -21 4>)) <vulture>
29104:29047 = 3.385 -48.668 --> -2/53 = -45.283 (dodifo-comma (~ratio, monzo=[-67 -9 35>)) <>
61153:61035 = 3.338 +19.303 --> 1/53 = 22.642 (vishnuzma/semisuper-comma (~ratio, monzo=[23 6 -14>)) <>
190735:190425 = 2.816 -25.457 --> -1/53 = -22.642 (enneadeca (~ratio, monzo=[-14 -19 19>)) <>
29558:29518 = 2.523 -25.165 --> -1/53 = -22.642 (vavoom-comma (~ratio, monzo=[-68 18 17>)) <>
687195:686304 = 2.246 -2.246 --> 0/53 = 0.000 (tricot-comma (~ratio, monzo=[39 -29 3>)) <>
32805:32768 = 1.954 -1.954 --> 0/53 = 0.000 (skhisma (exact ratio)) <helmholtz>
29543:29518 = 1.661 -1.661 --> 0/53 = 0.000 (counterschisma (~ratio, monzo=[-69 45 -1>)) <>
5820766:5815959 = 1.431 -46.714 --> -2/53 = -45.283 (septendecima (~ratio, monzo=[-52 -17 34>)) <>
274878:274658 = 1.384 +21.257 --> 1/53 = 22.642 (luna-comma/hemithirds-comma (~ratio, monzo=[38 -2 -15>)) <>
50031545:50000000 = 1.092 +21.550 --> 1/53 = 22.642 (minortone-comma/minortonma (~ratio, monzo=[-16 35 -17>)) <>
76294:76256 = 0.862 -23.503 --> -1/53 = -22.642 (ennealimma (~ratio, monzo=[1 -27 18>)) <ennealimmal>
2475880:2474715 = 0.815 +44.468 --> 2/53 = 45.283 (astro-comma (~ratio, monzo=[91 -12 -31>)) <>
225284:225180 = 0.799 +21.842 --> 1/53 = 22.642 (gaster-comma (~ratio, monzo=[-70 72 -19>)) <>
901016:900720 = 0.569 -23.211 --> -1/53 = -22.642 (kwazy (~ratio, monzo=[-53 10 16>)) <>
116450:116415 = 0.522 +44.761 --> 2/53 = 45.283 (whoosh (~ratio, monzo=[37 25 -33>)) <>
444089:444002 = 0.339 -68.264 --> -3/53 = -67.925 (egads (~ratio, monzo=[-36 -52 51>)) <>
450360:450284 = 0.292 -0.292 --> 0/53 = 0.000 (monzisma (~ratio, monzo=[54 -37 2>)) <monzismic>
162285244:162259277 = 0.277 -22.919 --> -1/53 = -22.642 (fortune (~ratio, monzo=[-107 47 14>)) <>
22300745:22297584 = 0.245 +67.679 --> 3/53 = 67.925 (gross (~ratio, monzo=[144 -22 -47>)) <>
38152042:38146973 = 0.230 +45.053 --> 2/53 = 45.283 (senior (~ratio, monzo=[-17 62 -35>)) <>
17179869:17179251 = 0.062 -45.345 --> -2/53 = -45.283 (raider (~ratio, monzo=[71 -99 37>)) <>
17763568:17763086 = 0.047 -67.971 --> -3/53 = -67.925 (pirate (~ratio, monzo=[-90 -15 49>)) <>
36185688:36185028 = 0.032 -90.598 --> -4/53 = -90.566 (viking (~ratio, monzo=[-251 69 61>)) <>
292300:292297 = 0.015 +22.626 --> 1/53 = 22.642 (kirnberger-atom (~ratio, monzo=[161 -84 -12>)) <atomic>
51475576:51475434 = 0.005 -384.910 --> -17/53 = -384.906 (selenia (~ratio, monzo=[-433 -137 280>)) <>
30916316:30916300 = 0.001 -135.850 --> -6/53 = -135.849 (quark (~ratio, monzo=[-573 237 85>)) <>
7-limit
ratio cents error edo cents name
28:27 = 62.961 +4.964 --> 3/53 = 67.925 (trienstonic-comma/septimal-third-tone) <trienstonic clan>
59049:57344 = 50.724 -5.441 --> 2/53 = 45.283 (harrison-comma) <septimal-meantone>
36:35 = 48.770 -3.487 --> 2/53 = 45.283 (septimal-diesis/septimal-quartertone/mint-comma) <mint>
49:48 = 35.697 +9.586 --> 2/53 = 45.283 (slendro diesis (7/6 : 8/7)) <slendro (rank-2), semiphore (rank-3)>
50:49 = 34.976 -12.334 --> 1/53 = 22.642 (tritonic diesis/jubilisma) <jubilismic>
64:63 = 27.264 -4.623 --> 1/53 = 22.642 (septimal-comma/archytas-comma) <archytas>
245:243 = 14.191 +8.451 --> 1/53 = 22.642 (sensamagic-comma) <sensamagic>
126:125 = 13.795 +8.847 --> 1/53 = 22.642 (starling-comma) <starling>
1728:1715 = 13.074 -13.074 --> 0/53 = 0.000 (orwellisma) <orwellismic>
225:224 = 7.712 -7.712 --> 0/53 = 0.000 (marvel-comma/septimal-kleisma) <marvel>
65625:65536 = 2.349 -2.349 --> 0/53 = 0.000 (horwell-comma) <horwell>
2401:2400 = 0.721 +21.920 --> 1/53 = 22.642 (breedsma) <breedsmic>
4375:4374 = 0.396 -0.396 --> 0/53 = 0.000 (ragisma) <ragismic>
250047:250000 = 0.325 +22.316 --> 1/53 = 22.642 (landscape-comma) <landscape>
11-limit
ratio cents error edo cents name
22:21 = 80.537 -12.613 --> 3/53 = 67.925 (undecimal-minor-semitone) <>
33:32 = 53.273 -7.990 --> 2/53 = 45.283 (undecimal-diesis/al-farabi-quartertone) <>
45:44 = 38.906 +6.377 --> 2/53 = 45.283 (undecimal-fifth-tone) <>
8192:8019 = 36.952 +8.331 --> 2/53 = 45.283 (pyth dim-5th: 11/8) <>
55:54 = 31.767 -9.125 --> 1/53 = 22.642 (telepathma) <>
56:55 = 31.194 +14.089 --> 2/53 = 45.283 (undecimal-diesis/konbini-comma) <>
99:98 = 17.576 -17.576 --> 0/53 = 0.000 (mothwellsma (9/7 : 14/11)) <mothwellsmic>
100:99 = 17.399 +5.242 --> 1/53 = 22.642 (ptolemisma (10/9 : 11/10)) <ptolemismic>
121:120 = 14.367 -14.367 --> 0/53 = 0.000 (biyatisma (11/10 : 12/11)) <biyatismic>
385:384 = 4.503 -4.503 --> 0/53 = 0.000 (keenanisma/undecimal-kleisma) <keenanismic>
540:539 = 3.209 -3.209 --> 0/53 = 0.000 (swetisma) <big-brother/swetismic>
4000:3993 = 3.032 +19.609 --> 1/53 = 22.642 (wizardharry-comma/pine-comma) <tertiaschis/larry>
5632:5625 = 2.153 -2.153 --> 0/53 = 0.000 (vishdel-comma) <vishdel>
3025:3024 = 0.572 -23.214 --> -1/53 = -22.642 (lehmerisma) <lehmerismic>
9801:9800 = 0.177 -22.818 --> -1/53 = -22.642 (kalisma/gauss-comma) <kalismic>
13-limit
ratio cents error edo cents name
40:39 = 43.831 +1.452 --> 2/53 = 45.283 (tridecimal-minor-diesis (5/3 : 13/8)) <>
65:64 = 26.841 -4.200 --> 1/53 = 22.642 (wilsorma (13/8 : 8/5)) <>
6656:6561 = 24.888 -2.246 --> 1/53 = 22.642 (13/8 : pyth aug-5th) <>
91:90 = 19.130 +3.512 --> 1/53 = 22.642 (biome-comma/superleap) <biosphere>
144:143 = 12.064 +10.577 --> 1/53 = 22.642 (grossma (18/11 : 13/8, 12/11 : 13/12)) <teff>
169:168 = 10.274 -10.274 --> 0/53 = 0.000 (buzurgisma/dhanvantarisma (13/12 : 14/13)) <buzurgismic/dhanvantarismic>
625:624 = 2.772 -2.772 --> 0/53 = 0.000 (tunbarsma) <>
676:675 = 2.563 -2.563 --> 0/53 = 0.000 (parizeksma/island-comma) <parizeksmic>
729:728 = 2.376 -2.376 --> 0/53 = 0.000 (squbema) <squbemic>
2200:2197 = 2.362 -2.362 --> 0/53 = 0.000 (petrma) <petrmic>
1575:1573 = 2.200 +20.442 --> 1/53 = 22.642 (nicola) <nicolic>
1001:1000 = 1.730 -1.730 --> 0/53 = 0.000 (sinbadma/fairytale-comma) <sinbadmic>
1716:1715 = 1.009 -23.651 --> -1/53 = -22.642 (lummic-comma) <lummic>
2080:2079 = 0.833 -0.833 --> 0/53 = 0.000 (ibnsinma) <ibnsinmic>
4096:4095 = 0.423 -0.423 --> 0/53 = 0.000 (schismina) <schisminic>
4225:4224 = 0.410 -0.410 --> 0/53 = 0.000 (leprechaun-comma) <leprechaun/abigail/newt/decoid/donar>
6656:6655 = 0.260 +22.381 --> 1/53 = 22.642 (jacobin-comma) <jacobin>
-------------------- end of coded printout ----------------
